1. Énergie 1

1.1. Énoncé

Retrouver une expression de l’ordre de grandeur de l’énergie de l’atome d’hydrogène {\(a_0\)} à partir du principe d’incertitude

1.2. Réponse

Rappelons le principe d’incertitude d’Heisenberg (formulation en ordre de grandeur) : \[\Delta p~\Delta x~\approx~\hbar\]

On fera ici : \[\Delta x\approx a\]

On peut également admettre que : \[\Delta p~\approx~\sqrt{2~m~E}\]

• \(E\) : énergie cinétique moyenne

D’après l’ordre de grandeur de l’énergie potentielle moyenne (loi de Coulomb) : \[E~=~\frac{q^2}{a_0}~\sim~\frac{e^2}{4\pi~\varepsilon_0}~\frac{1}{a_0}\]

Puis : \[a~\approx~\frac{4\pi~\varepsilon_0~\hbar^2}{2~m~e^2}\]

Cette expression, qui sera souvent rencontrée, représente de manière systématique un ordre de grandeur de l’énergie associée au mouvement des électrons.

2. Énergie 2

2.1. Énoncé

Soit \(\psi\) une solution approchée normalisée d’un hamiltonien \(\widehat{H}\) dont les solutions exactes sont :

\[\begin{aligned} &|0\rangle,~|1\rangle,~\dots,~|i\rangle\\ &E_0,~E_1,~\dots,~E_i\end{aligned}\]

Les valeurs propres \(E_i\) sont classées par ordre croissant d’énergies.

Les fonctions propres de \(\widehat{H}\) forment une base orthonormée, c’est-à-dire que l’on peut poser : \[|\psi\rangle~=~\sum_i c_i~|i\rangle\]

Calculer la valeur moyenne de \(\psi\) relativement à {\(\widehat{H}-E_0\)}.

2.2. Réponse

La valeur moyenne \(E\) de \(\psi\) est : \[E~=~\langle\psi^*|\widehat{H}|\psi\rangle\]

Comme \(\psi\) est normalisée, on peut écrire : \[E-E_0~=~\langle\psi^*|\hat{H}|\psi\rangle-E_0\langle\psi^*|\psi\rangle~=~\langle\psi^*|\hat{H}|\psi\rangle-E_0\langle\psi^*|E_0|\psi\rangle~=~\langle\psi^*|\hat{H}-E_0|\psi\rangle\]

On sait d’autre part que : \[|\psi\rangle~=~\sum_i c_i~|i\rangle\]

On peut écrire que :

\[\begin{aligned} \Big\{\sum_i c_i^*~\langle i|\Big\}~|\hat{H}-E_0|~\Big\{\sum_i c_i~|j\rangle\Big\}~ &=~\sum_i c_i^*~c_i~\big\{\langle i|\hat{H}|i\rangle-\langle i|E_0|i\rangle\big\}\\ &=\sum_ic_i^*~c_i~\big\{\langle i|E_i-E_0|i\rangle\big\}\\ &=~\sum_i c_i^*~c_i~\{E_i-E_0\}\end{aligned}\]

Remarque 1

Comme par hypothèse \(E_0<E_i\), la valeur moyenne de la solution approchée est toujours supérieure à l’énergie \(E_0\) de l’état fondamental.

Remarque 2

On dispose principalement de deux outils mathématiques d’optimisation des solutions selon que l’on part d’une solution approchée de l’hamiltonien ou d’une solution exacte de l’hamiltonien approché.

Ainsi, contrairement au calcul précédent, la méthode des perturbations procède de la manière suivante :

On a les solutions exactes {\(|i\rangle~;~E_i^0\)} d’un hamiltonien \(\widehat{H}_0\) et on cherche des solutions de \[\widehat{H}~=~\widehat{H}_0~+~\widehat{h}\]

Les valeurs propres \(E_i\) de \(\widehat{H}\) s’obtiennent sous la forme d’un développement aux ordres successifs 1, 2... : \[E_i~=~E_i^0+E_i^1+E_i^2+\dots\]

Avec : \[E_i^1~=~\langle i|\widehat{h}|i\rangle\quad;\quad E_i^2~=~\sum_{j\neq i}~\frac{\langle i|\widehat{h}|i\rangle^2}{E_i^0-E_j^0}\quad;\quad\dots\]

3. Énergie 3

3.1. Énoncé

Puits de potentiel : l’énergie potentielle en tant que perturbation.

Déterminer le niveau d’énergie dans un puits de potentiel (de largeur \(a\)) à une dimension de faible profondeur. Nous ferons l’hypothèse que : \[|U|~\ll~\frac{\hbar^2}{m~a^2}\qquad(\text{pour}~~ka\lessapprox 1)\]

3.2. Réponse

Rappelons l’expression de l’équation de Schrödinger dans le cas général : \[\frac{d^2\psi}{dx^2}~=~\frac{2~m}{\hbar^2}~\big\{U(x)-E\big\}~\psi\qquad(1)\]

Dans le second membre de (1), on peut négliger \(E\) dans la région du puits et considérer également que \(\psi\) est constante.

On peut admettre pour cette constante la valeur 1 sans restreindre la généralité de cette équation : \[\frac{d^2\psi}{dx^2}~=~\frac{2m}{\hbar^2}~U(x)\qquad(2)\]

Intégrons cette égalité sur \(dx\) entre deux points \(\pm~x_1\) tels que : \[a~\ll~x_1~\ll~\chi\qquad;\qquad\kappa=\frac{\sqrt{2~m~E}}{\hbar}\]

L’intégrale de \(U(x)\) convergeant, on peut étendre à droite l’intégration à toute la région allant de \(-\infty\) à \(+\infty\) : \[\frac{d\psi}{dx}\Big|_{-x_1}^{+x_1}~=~\frac{2~m}{\hbar^2}\int_{-\infty}^{+\infty}U(x)~dx\qquad(3)\]

Loin du puits, la fonction d’onde s’écrit : \[\psi~=~\exp(\pm~\kappa~x)\]

Après substitution dans (3) : \[-2~\kappa~=~\frac{2~m}{\hbar^2}\int_{-\infty}^{+\infty}U(x)~dx\]

ou : \[E~=~\frac{2~m}{\hbar^2}~\Big\{\int_{-\infty}^{+\infty}U(x)~dx\Big\}^2\qquad(4)\]

Nous voyons, ce qui est conforme à notre hypothèse, que la grandeur du niveau est effectivement une quantité petite d’ordre supérieur (du second) à la profondeur.

4. Spectroscopie 1

4.1. Énoncé

Calculer, en électron-volts (eV), l’énergie d’ionisation de l’atome d’hydrogène, connaissant \(\bar{\nu}\) = 1,5233 10\({^6}\) cm le nombre d’ondes de la raie rouge \(H_{\alpha}\) de la série de Balmer de l’hydrogène.

4.2. Solution

Le nombre d’ondes d’une raie du spectre de l’atome d’hydrogène est donné par : \[\bar{\nu}~=~R_H~\Big\{\frac{1}{n_1^2}-\frac{1}{n_2^2}\Big\}\qquad;\qquad n_2>n_1\]

• \(R_H\) : constante de Rydberg pour l’hydrogène

Rappelons les différentes séries du spectre de l’atome d’hydrogène :

\[\begin{aligned} &n_1=1,~n_2~\text{variable} &&\text{série de Lymann} &&\text{UV~lointain}\\ &n_1=2,~n_2~\text{variable} &&\text{série de Balmer} &&\text{UV~visible}\\ &n_1=3,~n_2~\text{variable} &&\text{série de Paschen} &&\text{IR~proche}\\ &n_1=4,~n_2~\text{variable} &&\text{série de Brackett} &&\text{IR~lointain}\\ &n_1=5,~n_2~\text{variable} &&\text{série de Pfund} &&\text{IR~très~lointain}\end{aligned}\]

4.2.1. Calcul de la constante de Rydberg

La raie rouge \(H_{\alpha}\) de la série de Balmer correspond aux valeurs \(n_1\) = 2 ; \(n_2\) = 3.

Son nombre d’ondes est : \[\bar{\nu}~=~R_H~\Big(\frac{1}{4}-\frac{1}{9}\Big)\quad\Rightarrow\quad R_H=1,096~77\times 10^7~\rm m^{-1}\]

4.2.2. Calcul de l’énergie d’ionisation

L’énergie d’ionisation est l’énergie qu’il faut fournir à l’électron de l’atome pris dans son état le plus lié (\(n_1=1\)) pour l’arracher complètement de l’atome (état libre \(n_2=\infty\)).

Cette énergie est celle des photons dont le nombre d’ondes est alors celui de la limite de la série de Lymann : \[\bar{\nu}_i~=~R_H~\Big(\frac{1}{1^2}-\frac{1}{\infty}\Big)~=~R_H\]

L’énergie est reliée au nombre d’ondes par : \[E~=~h~c~\bar{\nu}\]

• \(h\) : constante de Planck (\(6,626~07\times 10^{-34}~\rm J~s\))

• \(c\) : vitesse de la lumière (\(2,997~92\times 10^8~\rm m~s^{-1}\))

En ayant recours à la correspondance joule – électron-volt : \[1~\rm eV~=~1,602~176\times 10^{-19}~J\]

On obtient, tous calculs faits : \(E_i~=~13,6~\rm eV\)

5. Spectroscopie 2

5.1. Énoncé

Dans la série de plus courte longueur d’onde du spectre de l’atome d’hélium ionisé, la première raie a pour nombre d’ondes \(\bar{\nu}'=3,291~67\times 10^5~\rm m^{-1}\).

En déduire le rapport de la masse de l’électron à celle du noyau d’hydrogène.

\(H~=~1,008~\rm uma \quad ;\quad He~=~4,004~uma\)

5.2. Solution

1) Le numéro atomique de l’hélium est Z = 2.

Soit \(R_{He}\) la constante de Rydberg pour l’atome d’hélium ionisé, les nombres d’ondes des raies de la série de plus courte longueur d’onde ont pour expression : \[\bar{\nu}'~=~R_{He}~Z^2~\Big(\frac{1}{1^2}-\frac{1}{n^2}\Big)\]

Le nombre d’ondes de la première raie est : \[\bar{\nu}'~=~R_{He}\times 4~\Big(1-\frac{1}{4}\Big)~=~3~R_{He}\]

Numériquement : \(R_{He}=1,097~223\times 10^5~\rm m^{-1}\).

2) Les constantes de Rydberg pour les atomes d’hydrogène et d’hélium ionisé sont donnés par les formules respectives : \[R_H~=~\frac{2\pi^2~\mu_H~e^4}{h^3~c}\qquad;\qquad~R_{He}~=~\frac{2\pi^2~\mu_{He}~e^4}{h^3~c}\]

\(\mu_H\) et \(\mu_{He}\) étant respectivement les masses réduites de l’électron dans les atomes d’hydrogène et d’hélium : \[\frac{1}{\mu}=\frac{1}{m}+\frac{1}{M}~~\Rightarrow~~\mu=\frac{M~m}{M+m}\]

• \(m\) : masse au repos de l’électron

• \(M\) : masse du noyau considéré

\(R\) est donc proportionnel à \(\mu\) et on peut écrire : \[\frac{R_{He}}{R_H}~=~\frac{\mu_{He}}{\mu_H}~=~\frac{M_{He}~m}{M_{He}+m}~\frac{M_H+m}{M_H~m}\]

Tous calculs faits, on obtient : \[\frac{m}{M_H}~=~M_{He}~\frac{R_{He}-R_H}{M_{He}~R_H-M_H~R_{He}}\]

Et pour l’application numérique : \[\frac{m}{M_H}~=~\frac{1}{1835,7}\]

6. Relativité 1

6.1. Énoncé

1) Tenant compte de la variation de la masse avec la vitesse, on montrera que la masse \(m_0\) d’une particule est donnée par l’expression : \[m_0~c^2~=~\frac{1}{2}~\Big\{\frac{p^2~c^2}{E_c}-E_c\Big\}\]

• \(p\) : moment (quantité de mouvement)

• \(E_c\) : énergie cinétique (différence entre l’énergie totale et la masse au repos)

• \(c\) : vitesse de la lumière

2) L’expérience montre que, pour une certaine particule observée à haute altitude dans l’atmosphère : \[E_c~=~215~{\rm MeV}\qquad;\qquad p~c~=~325~\rm MeV\]

Entendre que la valeur de \(p\), évaluée en prenant pour unité {eV/c} est égale à \(325\times 10^6\).

Calculer la masse au repos de cette particule, ainsi que le rapport de la masse précédente à la masse au repos de l’électron (\(9,11\times 10^{-31}\) kg).

Indiquer de quelle particule il s’agit.

On rappelle que l’unité de masse employée en physique nucléaire (\(1,66\times 10^{-27}\) kg) équivaut à 931 MeV.

3) Calculer enfin le rapport de la vitesse de la particule à celle de la lumière.

6.2. Solutions

1) Nous allons calculer la quantité \(p^2~c^2\) : \[p^2~c^2~=~m^2~v^2~c^2~=~m^2~c^4~=~E^2~\beta^2\qquad(\text{avec}~\beta=v/c)\]

• \(E\) : énergie totale de la particule

On peut écrire : \[p^2~c^2~=~E^2-E^2~(1-\beta^2)~=~E^2-m^2~c^4~(1-\beta^2)~=~E^2-m_0^2~c^4\]

Or : \[E~=~E_c+m^2~c^2\]

Donc : \[p^2~c^2~=~E_c^2+2~E_c~m_0~c^2\]

Et finalement (ce qu’il fallait démontrer) : \[m_0c^2~=~\frac{1}{2}~(~\frac{p^2c^2}{E_c}-E_c~)\]

2) Appliquée au cas particulier proposé, cette formule donne : \[m_0~c^2~=~\frac{1}{2}~\Big(\frac{325^2}{215}-215\Big)~=~138~\rm MeV\]

Ou, en masse : \[m_0~=~\frac{138\times 1,66\times 10^{-27}}{931}~=~2,46\times 10^{-28}~\rm kg\]

Et on obtient ainsi : \[\frac{m_0}{m_e}~=~270\]

3) Nous partons de : \[p~c~=~m~v~c~=~m~c^2~\frac{v}{c}\qquad\text{avec}~:\quad m~c^2~=~E~=~m_0~c^2+E_c\]

Numériquement : \[p~c=325~{\rm MeV}\quad;\quad m~c^2=138~\rm MeV+215~MeV~=~353~MeV\]

Tous calculs faits : \[\frac{v}{c}~=~\frac{325}{353}~=~0,92\]

7. Perturbations 1

7.1. Énoncé

Le hamiltonien d’un système : \[\widehat{H}~=~\widehat{H_0}~+~\widehat{V}\]

est donné sous forme directe de matrices : \[\widehat{H_0}= \begin{pmatrix} a&0&0\\ 0&b&0\\ 0&0&b \end{pmatrix} \quad;\quad \widehat{V}= \begin{pmatrix} 0&0&\alpha\\ 0&0&\beta\\ \alpha&\beta&0 \end{pmatrix} \qquad a~\neq~b\quad;\quad\alpha~\neq~\beta\]

Appliquer la théorie des perturbations au calcul des niveaux d’énergie.

7.2. Solution

La matrice étant diagonale \(\widehat{H_0}\) a pour valeurs propres (évident) :

• \(\mathcal{E}_0=a\)  :  valeur propre simple

• \(\mathcal{E}_1=b\)  :  valeur propre double

\[\text{det}~\widehat{H}~=~ \begin{vmatrix} a-\lambda&0&0\\ 0&b-\lambda&0\\ 0&0&b-\lambda \end{vmatrix} ~=~(a-\lambda)~(b-\lambda)^2~=0\]

Vecteurs propres respectifs :

•   \(|\varphi_0\rangle\) = (1, 0, 0)

• \(|\varphi_{1,1}\rangle\) = (0, 1, 0)\(|\varphi_{1,2}\rangle\) = (0, 0, 1)

7.2.1. Cas de la valeur propre simple (a)

Calcul de l’énergie à l’ordre 1 : \(E_0^{(1)}\) ou \(\langle\varphi_0~|\widehat{V}|~\varphi_0\rangle\) : \[(1~0~0)\times \begin{pmatrix} 0&0&\alpha\\ 0&0&\beta\\ \alpha&\beta&0 \end{pmatrix} \times(1~0~0)~=~(0~0~\alpha)\times(1~0~0)~=~0\]

Calcul de l’énergie à l’ordre 2, \(E_0^{(2)}\) : \[E_0^{(2)}~=~\sum_{j=1,2}\frac{|\langle\varphi_{1,j}|\widehat{V}|\varphi_0\rangle|^2}{E_0^{(0)}-E_1^{(0)}} ~=~\frac{|\langle\varphi_{1,1}~|\widehat{V}|~\varphi_0\rangle|^2}{a-b} ~+~\frac{|\langle\varphi_{1,2}~|\widehat{V}|~\varphi_0\rangle|^2}{a-b}\]

Premières multiplications matricielles : \[(0~1~0)\times \begin{pmatrix} 0&0&\alpha\\ 0&0&\beta\\ \alpha&\beta&0 \end{pmatrix} \times(1~0~0)~=~(0~0~\beta)\times(1~0~0)~=~0\]

Deuxièmes multiplications matricielles : \[(0~0~1)\times \begin{pmatrix} 0&0&\alpha\\ 0&0&\beta\\ \alpha&\beta&0 \end{pmatrix} \times(1~0~0)~=~(\alpha~\beta~0)\times(1~0~0)~=~\alpha\]

On a donc : \[E_0^{2}~=~\frac{\alpha^2}{a-b}\]

Et il vient : \[E_0~\approx~a~+~\frac{\alpha^2}{a-b}\]

Fonction propre à l’ordre 1, \(|\psi_0{(1)}\rangle\) : \[|\psi_0^{(1)}\rangle~=~\sum_{j=1,2}\frac{\langle\varphi_{1,j}~|\widehat{V}|~\varphi_0\rangle}{E_0^{(0)}-E_1^{(0)}}~|~\varphi_{1,j}\rangle\]

Ce qui donne (deux termes) : \[|\psi_0^{(1)}\rangle ~=~\frac{\langle\varphi_{1,1}~|\widehat{V}|~\varphi_0\rangle}{a-b}~|~\varphi_{1,1}\rangle ~+~\frac{\langle\varphi_{1,2}~|\widehat{V}|~\varphi_0\rangle}{a-b}~|~\varphi_{1,2}\rangle\]

Seul subsiste le deuxième terme : \[|\psi_0^{(1)}\rangle~=~\frac{\alpha}{a-b}~|~\varphi_{1,2}\rangle\]

On a donc : \[|\psi_0~\rangle~=~|\varphi_0~\rangle~+~\frac{\alpha}{a-b}~|~\varphi_{1,2}\rangle\]

7.2.2. Cas de la valeur propre double (b)

Nous faisons tout d’abord la restriction \(\widehat{V}_1\) de \(\widehat{V}\) au sous-espace de dégénérescence.

C’est une matrice \(2\times2\) : \[\widehat{V}_1~=~ \begin{pmatrix} 0&d\\ d&0 \end{pmatrix}\]

\(\widehat{V}\) agit sur un espace à trois dimensions.

\(\widehat{V_1}\) agit sur un espace à deux dimensions.

Calcul des valeurs propres : \[\text{det}~\widehat{V_1}~=~ \begin{vmatrix} -\lambda&d\\ d&-\lambda \end{vmatrix} ~=~\lambda^2-d^2~=~(\lambda+d)~(\lambda-d)~=~0\]

D’où les deux valeurs propres distinctes : \(\lambda=\pm~d\)

Dans la restriction de l’espace de dimension 3 à l’espace de dimension 1 :

• le vecteur (0, 1, 0) correspond au vecteur (1, 0) ;

• le vecteur (0, 0, 1) correspond au vecteur (0, 1).

La matrice de \(\widehat{V_1}\) a pour valeurs propres {\(\pm~d\)} et les vecteurs propres suivants : \[\frac{1}{\sqrt{2}}~\{(1,~0)~\pm~d~(0,~1)\}\]

La \(\sqrt{2}\) a été introduite pour la normalisation du vecteur : \[\frac{1}{\sqrt{2}}~\{|\varphi_{1,1}\rangle~+~|\varphi_{1,2}\rangle\}\quad\text{et}\quad \frac{1}{\sqrt{2}}~\{|\varphi_{1,1}\rangle~-~|\varphi_{1,2}\rangle\}\]

Les énergies et les vecteur propres de l’opérateur \(\widehat{H}\) étant respectivement notés : \[E_0~;~E_+~\text{et}~E_-\quad\rightarrow\quad|\psi_1\rangle~;~|\psi_+\rangle~\text{et}~|\psi_-\rangle\]

On a donc : \[E_{\pm}^{(1)}~=~\pm~d\quad\Rightarrow\quad E_{\pm}~\approx~a~\pm~d\]

Avec : \[\begin{aligned} |\psi_+^{0}\rangle~=~\frac{1}{\sqrt{2}}~\{|\varphi_{1,1}\rangle~+~|\varphi_{1,2}\rangle\}\\ |\psi_-^{0}\rangle~=~\frac{1}{\sqrt{2}}~\{|\varphi_{1,1}\rangle~-~|\varphi_{1,2}\rangle\} \end{aligned}\]

8. Puits de potentiel 1

8.1. Énoncé

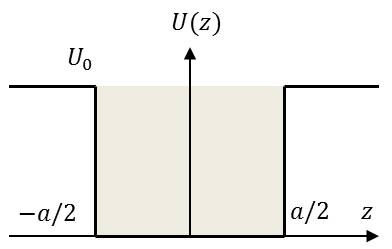On considère une particule dans un puits de potentiel non infini schématisé figure ci-contre.

Soit la fonction d’onde dérivant d’un état stationnaire d’énergie E : \[\Psi(x,~t)~=~\varphi(x)~\exp\Big(-i~\frac{E~t}{\hbar}\Big)\]

Avec :

\[\begin{aligned} \varphi~=~&\varphi_1(z) && z\in~\Big]-\infty~;~\frac{a}{2}\Big] &&(R1)\\ &\varphi_2(z) && z\in~\Big[-\frac{a}{2}~;~\frac{a}{2}\Big] &&(R2)\\ &\varphi_2(z) && z\in~\Big[\frac{a}{2}~;~\infty\Big[ &&(R3)\end{aligned}\]

1) Donner les solutions de l’équation de Schrödinger indépendante du temps dans le puits et à l’extérieur.

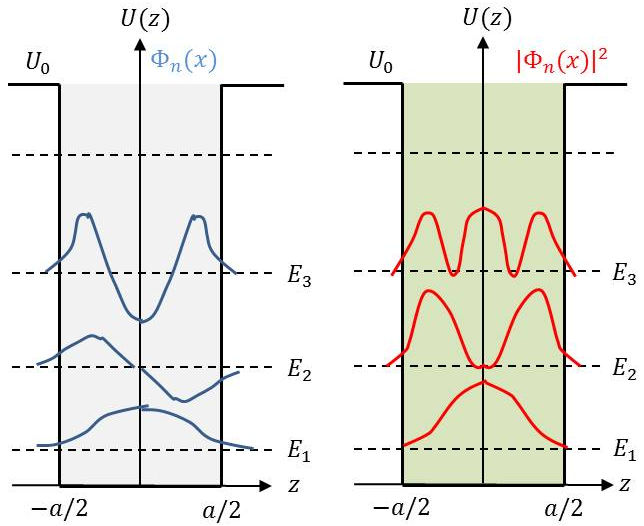
2) Tracer les fonctions d’onde ainsi que les probabilités de présence de la particule.

8.2. Solution

Expression de l’équation de Schrödinger dans chacune des régions (hypothèse \(E<U_0\)).

Posons : \[k~=~\frac{\sqrt{2~m~E}}{\hbar}\qquad;\qquad q~=~\frac{2~m~\sqrt{U_0-E}}{\hbar}\]

Les trois équations différentielles ont pour expressions :

\[\begin{aligned} \frac{\partial^2\varphi_1(z)}{\partial z^2}~&=~\frac{2~m~(U_0-E)}{\hbar^2}~\varphi_1(z)~=~q^2~\varphi_1(z) &&(R_1)\\ \frac{\partial^2\varphi_2(z)}{\partial z^2}~&=~-\frac{2~m~E)}{\hbar^2}~\varphi_2(z)~=~-k^2~\varphi_2(z) &&(R_2)\\ \frac{\partial^2\varphi_3(z)}{\partial z^2}~&=~\frac{2~m~(U_0-E)}{\hbar^2}~\varphi_3(z)~=~q^2~\varphi_3(z) &&(R_3)\end{aligned}\]

Dont les solutions classiques sont :

\[\begin{aligned} &\varphi_1(z)~=~A~\exp(q~z)+B~\exp(-q~z)\\ &\varphi_2(z)~=~C~\exp(i~k~z)+D~\exp(-i~k~z)\\ &\varphi_3(z)~=~E~\exp(q~z)+F~\exp(-q~z)\end{aligned}\]

Suivant que la fonction d’onde est symétrique ou antisymétrique, on aura :

\[\begin{aligned} &\text{symétrie}~: &&A=F &&C=D\\ &\text{antisymétrie}~: &&A=-F &&C=-D\end{aligned}\]

En réalité, comme la probabilité de présence ne peut être infinie, on doit se trouver en : \[\exp(q~z)~;~z<0\qquad\text{et}\qquad\exp(-q~z)~;~z>0\]

D’où les deux groupes de solutions : \[\left\{ \begin{aligned} &\varphi_1~=~A~\exp(q~z)\\ &\varphi_2~=~B~\cos(k~z)\\ &\varphi_3~=~A~\exp(-q~z)\\ \end{aligned} \right. \qquad\qquad \left\{ \begin{aligned} &\varphi_1~=~A~\exp(q~z)\\ &\varphi_2~=~B~\sin(k~z)\\ &\varphi_3~=~A~\exp(-q~z)\\ \end{aligned} \right.\]

Noter que la probabilité de présence est représentée par \(|\Phi_n(z)|^2\) (figure ci-dessus).