1. Introduction

Considérons une fonction \(\Phi(x,y,z)\) sur \(\mathbb R\) et définie dans un domaine \(D\subset \mathbb R^3\). En chaque point \(M\) de \(D\), cette fonction définit un champ scalaire dans \(D\).

Supposons maintenant que l’on puisse trouver en chaque point de \(M(x,y,z)\in D\) des expressions : \[A_x(x,y,z)~;~A_y(x,y,z)~;~A_z(x,y,z)\]

À tout point M peut être associé un vecteur de la forme : \[\overrightarrow{A}_M=\vec{i}~A_x+\vec{j}~A_y+\vec{k}~A_z\]

On dit qu’il existe alors un champ vectoriel ou champ de vecteurs.

Ces fonctions peuvent varier parfois avec le temps. On peut alors définir des dérivées de \((A_x,~A_y,~A_z)\) par rapport au temps en restant spatialement au même point.

Supposons que l’on passe d’un point \(M\) en un point \(M'\), les vecteurs \(\vec{i},~\vec{j},~\vec{k}\) étant constants. Il s’ensuit une variation (hypothèse du repère cartésien): \[\overrightarrow{dA}=\vec{i}~dA_x+\vec{j}~dA_y+\vec{k}~dA_z\]

Avec : \[\left\{ \begin{aligned} dA_x&=\frac{\partial A_x}{\partial x}~dx+\frac{\partial A_x}{\partial y}~dy+\frac{\partial A_x}{\partial z}~dz \\ dA_y&=\frac{\partial A_y}{\partial x}~dx+\frac{\partial A_y}{\partial y}~dy+\frac{\partial A_y}{\partial z}~dz \\ dA_z&=\frac{\partial A_z}{\partial x}~dx+\frac{\partial A_z}{\partial y}~dy+\frac{\partial A_z}{\partial z}~dz \end{aligned} \right.\]

2. Fonctions de points

2.1. Gradient

Supposons qu’en tout point de \(D\), il existe une fonction \(\Phi(x,y,z)\) continue et à dérivée première continue.

Du point \(M(x,~y,~z)\) au point voisin \(M'(x+dx,~y+dy,~z+dz)\), la fonction \(\Phi\) subit une variation : \[d\Phi=\frac{\partial\Phi}{\partial x}~dx+\frac{\partial\Phi}{\partial y}~dy+\frac{\partial\Phi}{\partial z}~dz\]

On obtient ainsi les composantes d’un vecteur appelé gradient de \(\Phi\).

Introduisant à présent un vecteur \(\overrightarrow{dM}(dx,~dy,~dz)\), on peut écrire : \[d\Phi=\overrightarrow{\rm grad}~\Phi\centerdot\overrightarrow{dM}\]

On dit qu’il s’agit de la définition intrinsèque du gradient.

En coordonnées cartésiennes, puis en coordonnées généralisées, on écrira : \[\overrightarrow{\rm grad}~\Phi=\vec{i}~\frac{\partial\Phi}{\partial x}+\vec{j}~\frac{\partial\Phi}{\partial y}+\vec{k}~\frac{\partial\Phi}{\partial z}=\overrightarrow{e}_i ~\frac{\partial\Phi}{\partial x}_i\]

Nous pourrons alors associer à la définition intrinsèque une interprétation géométrique du gradient :

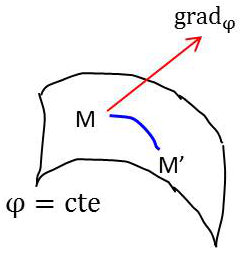Soit la surface d’équation \(\Phi(x,y,z)=cte\).

En un point M de cette surface, on peut définir un vecteur \(\overrightarrow{\rm grad}~\Phi\).

Pour un déplacement d’un point \(M\) en un point \(M'\) de la surface : \[d\Phi=\overrightarrow{\rm grad}~\Phi\centerdot\overrightarrow{dM}=0\quad\Rightarrow\quad\overrightarrow{\rm grad}~\Phi~\perp~\overrightarrow{MM'}\]

Le vecteur \(\overrightarrow{\rm grad}~\Phi\) est donc normal aux surfaces. Celles-ci sont appelées surfaces équipotentielles ou surfaces de niveau.

2.2. Divergence

Soit un vecteur : \[\overrightarrow{V}=\vec{i}~V_x+\vec{j}~V_y+\vec{k}~V_z\]

La fonction divergence est un scalaire défini sur ce vecteur par : \[{\rm div}\overrightarrow{V}=\frac{\partial V_x}{\partial x}+\frac{\partial V_y}{\partial y}+\frac{\partial V_z}{\partial z}\]

Montrons à présent que : \[{\rm div}\overrightarrow{V}=\vec{i}~\frac{\partial\overrightarrow{V}}{\partial x}+\vec{j}~\frac{\partial\overrightarrow{V}}{\partial y}+\vec{k}~\frac{\partial\overrightarrow{V}}{\partial z}\]

En effet : \[{\rm div}\overrightarrow{V}=\vec{i}\centerdot\{\vec{i}~\frac{\partial V_x}{\partial x}+\vec{j}~\frac{\partial V_y}{\partial y}+\vec{k}~\frac{\partial V_z}{\partial z}\}+\vec{j}\centerdot\{\dots\}+\vec{k}\centerdot\{\dots\}\]

Avec : \[\vec{i}\centerdot\vec{j}=\vec{i}\centerdot\vec{k}=\vec{j}\centerdot\vec{k}=0\]

On peut donc écrire en coordonnées généralisées : \[{\rm div}\overrightarrow{V}=\overrightarrow{e}_i\centerdot\frac{\partial\overrightarrow{V}}{\partial x_i}\qquad\text{cqfd}\]

Nous pouvons en faire une interprétation physique (voir figure ci-contre) :

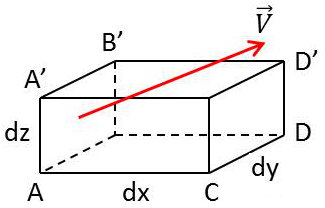Un fluide est animé d’une vitesse \(V\). Évaluons le volume de fluide qui sort de ce parallélépipède en une unité de temps (seconde) :

Face \(ABB'A'\) \[\text{Entrée}~:~V_x~dy~dz\qquad\text{Sortie}~:~-V_x~dy~dz\]

Face \(CDD'C'\) \[\text{Sortie}~:~(V_x+\frac{\partial V_x}{\partial x}~dx)~dy~dz\]

En définitive, il sort du parallélépipède et dans cette direction la quantité : \[\frac{\partial V_x}{\partial x}~dx~dy~dz=\frac{\partial V_x}{\partial x}~d\tau\]

De même pour les autres faces.

Le volume du fluide sortant est alors : \({\rm div}\overrightarrow{V}~d\tau\)

Si V est une constante, on a alors :\({\rm div}\overrightarrow{V}=0\)

2.3. Rotationnel

Par définition, un rotationnel est un vecteur noté \(\overrightarrow{\rm rot}~\overrightarrow{V}\) associé à un autre vecteur par un déterminant :

\[\begin{aligned} \overrightarrow{\rm rot}~\overrightarrow{V}&= \begin{bmatrix} \vec{i}&\vec{j}&\vec{k}\\ \partial /\partial x&\partial /\partial y&\partial /\partial z\\ V_x&V_y&V_z\\ \end{bmatrix}\\ \overrightarrow{\rm rot}~\overrightarrow{V}&= \vec{i}\wedge\frac{\partial\overrightarrow{V}}{\partial x}+\vec{j}\wedge\frac{\partial\overrightarrow{V}}{\partial y}+\vec{k}\wedge\frac{\partial\overrightarrow{V}}{\partial z}\end{aligned}\]

Avec: \[\frac{\partial\overrightarrow{V}}{\partial x}=\vec{i}~\frac{\partial V_x}{\partial x}+\vec{j}~\frac{\partial V_y}{\partial x}+\vec{k}~\frac{\partial V_z}{\partial x}\qquad\text{et permutations}\]

En coordonnées généralisées : \[\overrightarrow{\rm rot}\overrightarrow{V}=\overrightarrow{e}_i\wedge\frac{\partial\overrightarrow{V}}{\partial x_i}\]

3. Identités vectorielles

Nous mettons ici en valeur quelques identités remarquables.

Première identité

\[\begin{aligned} &{\rm div}(m~\overrightarrow{V})=\overrightarrow{e}_i\centerdot\frac{\partial}{\partial x_i}(m~\overrightarrow{V})=\overrightarrow{e}_i\centerdot\Big\{\frac{\partial m}{\partial x_i}~\overrightarrow{V}+m~\frac{\partial\overrightarrow{V}}{\partial x_i}\Big\}\\ &{\rm div}(m~\overrightarrow{V})=\Big(\frac{\partial m}{\partial x_i}~\overrightarrow{e}_i\Big)\centerdot\overrightarrow{V}+m~\Big(\overrightarrow{e}_i\centerdot\frac{\partial\overrightarrow{V}}{\partial x_i}\Big)\\ &{\rm div}(m~\overrightarrow{V})=\overrightarrow{\rm grad}~m\centerdot\overrightarrow{V}+m~{\rm div}\overrightarrow{V}\end{aligned}\]

Deuxième identité

\[\begin{aligned} &\overrightarrow{\rm rot}(m~\overrightarrow{V})=\overrightarrow{e}_i\wedge(m~\overrightarrow{V})=\overrightarrow{e}_i\wedge\Big(\frac{\partial m}{\partial x_i}~\overrightarrow{V}\Big)+\overrightarrow{e}_i\wedge\Big(m~\frac{\partial\overrightarrow{V}}{\partial x_i}\Big)\\ &\overrightarrow{\rm rot}(m~\overrightarrow{V})=\Big(\frac{\partial m}{\partial x_i}~\overrightarrow{e}_i\Big)\wedge\overrightarrow{V}+m~\Big(\overrightarrow{e}_i\wedge\frac{\partial\overrightarrow{V}}{\partial x_i}\Big)\\ &\overrightarrow{\rm rot}(m~\overrightarrow{V})=\overrightarrow{\rm grad}~m\wedge\overrightarrow{V}+m~\overrightarrow{\rm rot}~\overrightarrow{V}\end{aligned}\]

Troisième identité

\[\begin{aligned} &{\rm div}(\overrightarrow{U}\wedge\overrightarrow{V})=\overrightarrow{e}_i\centerdot\frac{\partial}{\partial x_i}~(\overrightarrow{U}\wedge\overrightarrow{V})=\Big[\overrightarrow{e}_i,~\frac{\partial\overrightarrow{U}}{\partial x_i},~\overrightarrow{V}\Big]+\Big[\overrightarrow{e}_i,~\overrightarrow{U},~\frac{\partial\overrightarrow{V}}{\partial x_i}\Big]\\ &{\rm div}(\overrightarrow{U}\wedge\overrightarrow{V})=\overrightarrow{V}\centerdot\Big(\overrightarrow{e}_i\wedge\frac{\partial\overrightarrow{U}}{\partial x_i}\Big)+\overrightarrow{U}\centerdot\Big(\overrightarrow{e}_i\wedge\frac{\partial\overrightarrow{V}}{\partial x_i}\Big)\\ &{\rm div}(\overrightarrow{U}\wedge\overrightarrow{V})=\overrightarrow{V}\centerdot\overrightarrow{\rm rot}~\overrightarrow{U}+\overrightarrow{U}\centerdot\overrightarrow{\rm rot}~\overrightarrow{V}\end{aligned}\]

4. Laplaciens

4.1. Laplacien d’un scalaire \(\Phi\)

Par définition, le laplacien du scalaire \(\Phi\) est la quantité : \[\Delta\Phi={\rm div}(\overrightarrow{\rm grad}~\Phi)\]

En coordonnées cartésiennes : \[\Delta\Phi=\overrightarrow{e_i}\centerdot\Big\{\frac{\partial}{\partial x_i}\Big(\overrightarrow{e_j}~\frac{\partial\Phi}{\partial x_j}\Big)\Big\}=\overrightarrow{e_i}\centerdot\overrightarrow{e_j}~\frac{\partial^2\Phi}{\partial x_i~\partial x_j}\]

Analytiquement : \[\Delta\Phi=\frac{\partial^2\Phi}{\partial x^2}+\frac{\partial^2\Phi}{\partial y^2}+\frac{\partial^2\Phi}{\partial z^2}\]

4.2. Laplacien d’un vecteur V

Par définition : \[\Delta\overrightarrow{V}=\overrightarrow{\rm grad}~({\rm div}\overrightarrow{V})-\overrightarrow{\rm rot}~\overrightarrow{\rm rot}(\overrightarrow{V})\]

En coordonnées cartésiennes : \[\Delta\overrightarrow{V}=\overrightarrow{e_i}~\frac{\partial}{\partial x_i}\Big(\overrightarrow{e_j}\centerdot\frac{\partial\overrightarrow{V}}{\partial x_j}\Big)-\overrightarrow{e_i}\wedge\frac{\partial}{\partial x_i}\Big(\overrightarrow{e_j}\wedge\frac{\partial\overrightarrow{V}}{\partial x_j}\Big)\]

On a donc : \[\Delta\overrightarrow{V}=\overrightarrow{e_i}~\frac{\partial}{\partial x_i}\Big(\overrightarrow{e_j}\centerdot\frac{\partial\overrightarrow{V}}{\partial x_j}\Big)-\Big(\overrightarrow{e_i}~\frac{\partial^2\overrightarrow{V}}{\partial x_i~\partial x_j}\Big)\centerdot\overrightarrow{e}_j+(\overrightarrow{e_i}\centerdot\overrightarrow{e_j})~\frac{\partial^2\overrightarrow{V}}{\partial x_i~\partial x_j}\]

En réorganisant l’écriture : \[\Delta\overrightarrow{V}=(\overrightarrow{e_i}\centerdot\overrightarrow{e_j})~\frac{\partial^2\overrightarrow{V}}{\partial x_i~\partial x_j}-\Big(\overrightarrow{e_i}~\frac{\partial^2\overrightarrow{V}}{\partial x_i~\partial x_j}\Big)\centerdot\overrightarrow{e_j}+(\overrightarrow{e_i}\centerdot\overrightarrow{e_j})~\frac{\partial\overrightarrow{V}}{\partial x_j}\]

Et dans une écriture classique sans indices : \[\Delta\overrightarrow{V}=\frac{\partial^2\overrightarrow{V}}{\partial x^2}+\frac{\partial^2\overrightarrow{V}}{\partial y^2}+\frac{\partial^2\overrightarrow{V}}{\partial z^2}\]

5. Champs de rotationnels et de gradients

Nous énoncerons sans démonstration deux conditions nécessaires et suffisantes :

1. Pour qu’un champ de vecteurs soit un champ de gradient dans un domaine \(D\), il faut et il suffit que le rotationnel soit nul. \[\overrightarrow{E}=\overrightarrow{\rm grad}~\Phi\qquad\Leftrightarrow\qquad\overrightarrow{\rm rot}~\overrightarrow{E}=\overrightarrow{0}\]

2. Pour qu’un champ de vecteurs soit un champ de rotationnel dans un domaine \(D\), il faut et il suffit qu’il soit à divergence nulle. \[\overrightarrow{B}=\overrightarrow{\rm rot}~\overrightarrow{A}\qquad\Leftrightarrow\qquad~{\rm div}\overrightarrow{B}=0\]