1. Notions de coordonnées généralisée

Un point matériel est caractérisé par six paramètres :

– Trois paramètres de position \(x,~y,~z\) : \[\overrightarrow{OM}=\overrightarrow{r}\]

– Trois paramètres de vitesse \(v_x,~v_y,~v_z\) : \[\overrightarrow{V}=\frac{d\overrightarrow{r}}{dt}\]

Un système à \(N\) points a \(3~N\) degrés de liberté : \((x_1,~y_1,~z_1,~\dots,~x_N,~y_N,~z_N)\).

On peut prendre les coordonnées généralisées \(q^i\), \(i=(1,~2,~\dots,~N)\) définies par : \[q^i=f^1(x_1,~y_1,~z_1,~\dots,~x_N,~y_N,~z_N)\]

On adoptera alors le système des vitesses généralisées : \[\dot{q}^i=\frac{dq^i}{dt}\]

On connaît l’état d’un système dès que l’on connaît \(q^i\) et \(\dot{q}^i\).

Les équations du mouvement permettent de connaître l’état du système à un instant quelconque \(t>t_{initial}\). Elles sont de la forme : \[f(q^i,~\dot{q}^i,~t)=0\]

c’est-à-dire 3 N équations du deuxième ordre (théorème de Cauchy).

2. Principe de moindre action

Le principe de moindre action est fondamental en mécanique analytique. Appelé encore principe de Hamilton, il a été énoncé ainsi en 1840 :

Tout système mécanique à \(s\) degrés de liberté (\(s\) fini) est caractérisé par une fonction : \[L(q^1,~q^2,~\dots q~^s~;~\dot{q}^1,~\dot{q}^2,~\dots,~\dot{q}^s~;~t)\]

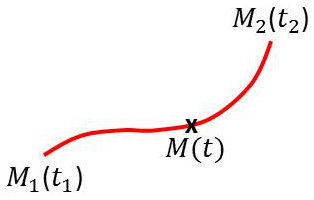
telle que, aux instants \(t_1\) et \(t_2\), le système occupe les positions définies par : \[\left\{ \begin{aligned} q^1,~q^2,~\dots,~q^s~;~\dot{q}^1,~\dot{q}^2,~\dots,~\dot{q}^s~;~t=t_1\\ q^1,~q^2,~\dots,~q^s~;~\dot{q}^1,~\dot{q}^2,~\dots,~\dot{q}^s~;~t=t_2 \end{aligned} \right.\]

Le système se déplace alors de telle sorte que : \[S=\int_{t1}^{t2} L~dt\quad\text{soit extrêmale.}\]

\(L\) est le lagrangien du système et \(S\) l’action du système :

\[\begin{aligned} M_1~:~(q^1,~q^2,~\dots,~q^s)~~(\dot{q}^1,~\dot{q}^2,~\dots,~\dot{q}^s)\\ M_2~:~(q^1,~q^2,~\dots,~q^s)~~(\dot{q}^1,~\dot{q}^2,~\dots,~\dot{q}^s)\end{aligned}\]

La courbe de l’espace des configurations doit être telle que \(S\) soit extrémale.

On utilise souvent l’espace des états à \(2~s\) dimensions \(M_1(q^1,~q^2,~\dots,~q^s,~\dot{q}^1,~\dot{q}^2,~\dots,~\dot{q}^s)\).

3. Équations de Lagrange

Écrivons que : \[S=\int_{t1}^{t2} L~dt\quad\text{est extrémale.}\]

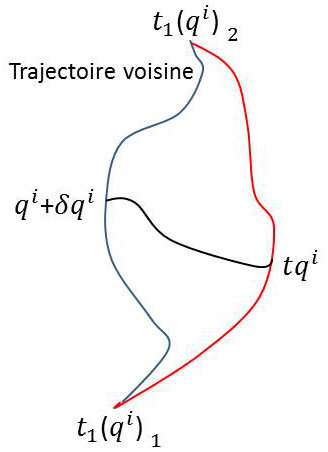
C’est à dire que la variation première \(\delta S\) est nulle : \[\delta S=\int_{t1}^{t2}\delta L~dt=0\qquad t_1,~t_2~\text{ fixés}\]

c’est-à-dire :

\[\begin{aligned} &\int_{t1}^{t2} \Big(\frac{\partial L}{\partial q^i}~\delta q^i+\frac{\partial L}{\partial\dot{q}^i}\delta\dot{q}^i\Big)~dt=0\qquad \delta\dot{q}=\delta\Big(\frac{dq}{dt}\Big)\\ &\frac{dq^i}{dt}=\lim\frac{(q^i+\Delta q^i)-q^i}{\Delta t}\qquad\text{quand }~\Delta t\rightarrow 0\\ &\delta\Big(\frac{dq^i}{dt}\Big)=\lim\frac{\delta (q^i+\Delta q^i)-\delta q^i}{\Delta t}=d\Big(\frac{\delta q^i}{dt}\Big)\end{aligned}\]

On voit que les opérateurs \(d\) et \(\delta\) : \[\delta\Big(\frac{dq^i}{dt}\Big)=\frac{d}{dt}(\delta q^i)\]

On a donc : \[\int_{t1}^{t2} \Big\{\frac{\partial L}{\partial q^i}~q^i+\frac{\partial L}{\partial\dot{q}^i}~\frac{d}{dt}(\dot{q}^i)\Big\}~dt=0\]

En intégrant le premier terme par parties : \[\int_{t1}^{t2} \frac{\partial L}{\partial q^i}~\frac{d}{dt}(\delta q^i)~dt= \Big[\frac{\partial L}{\partial\dot{q}^i}~\delta q^i\Big]_{t1}^{t2} -\int_{t1}^{t2} \delta q^i\frac{d}{dt}~\Big(\frac{\partial L}{\partial\dot{q} ^i}\Big)~dt\]

Le premier terme est nul, car : \[(\delta q^i)_{t_1}=(\delta q^i)_{t_2}\]

On a donc :

\[\begin{aligned} &\int_{t1}^{t2}\frac{\partial L}{\partial q^i}~\delta q^i~dt-\frac{d}{dt}\Big(\frac{\partial L}{\partial\dot{q}^i}\Big)~\delta q^i~dt=0\\ &\int_{t1}^{t2} \Big\{\frac{d}{dt}\Big(\frac{\partial L}{\partial\dot{q}^i}\Big)-\frac{\partial L}{\partial q^i}\Big\}~\delta q^i~dt=0\end{aligned}\]

Comme ceci est vrai quelque soit \(\delta q^i\), on obtient : \[\frac{d}{dt}\Big(\frac{\partial L}{\partial\dot{q}^i}\Big)-\frac{\partial L}{\partial q^i}=0\]

Donc, si à l’instant initial les paramètres \(q^i\) et \(\dot{q}^i\) sont connus, ils seront connus tout le temps.

Remarque

Il n’est pas nécessaire que la fonction \(L(q,~\dot{q},~t)\) soit totalement définie. Considérons en effet la fonction \(L'\) : \[L'(q^i,~\dot{q}^i,~t)=L(q^i,~\dot{q}^i,~t)+\frac{d}{dt}\big[f(q^i,~t)\big]\]

On a donc : \[S'=\int_{t1}^{t2}L'(q^i,~\dot{q}^i,~t)~dt= \int_{t1}^{t2} L(q^i,~\dot{q}^i,~t)~dt+\int_{t1}^{t2}\frac{d}{dt}\big[f(q^i,~t)\big]~dt\]

C’est-à-dire : \[S'=S+\big[f(q^i,t)\big]_{t2}-\big[f(q^i,t)\big]_{t1}\]

Comme les deux derniers termes sont des constantes : \[\Delta S=\Delta S'\]

4. Repères galiléens

4.1. Lagrangien d’un point matériel libre

On admet que l’espace est homogène par rapport à un repère galiléen, qu’il est isotrope et que le temps est uniforme.

En adoptant la notation \(L(\overrightarrow{r},~\overrightarrow{v},~t)\), nous précisons ces trois notions :

• Homogénéité :   \(L(\overrightarrow{v},~t) \quad L\) indépendant de \(r\)

• Uniformité(t) :    \(L(\overrightarrow{v}) \qquad L\) indépendant de \(t\)

• Isotropie :           \(L(\overrightarrow{v}^2)\)

On a donc : \[\frac{d}{dt}\Big(\frac{\partial L}{\partial\overrightarrow{v}}\Big)-\frac{\partial L}{\partial\overrightarrow{r}}=0\quad\Rightarrow\quad \frac{d}{dt}\Big\{\frac{\partial L(v^2)}{\partial\overrightarrow{v}}\Big\}=0\]

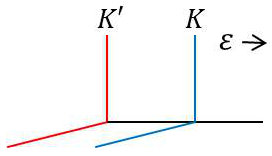Soit un repère \(K\) glissant sur un repère \(K'\) avec une petite vitesse \(\overrightarrow{\varepsilon}\) : \[\overrightarrow{v'}=\overrightarrow{v}+\overrightarrow{\varepsilon}\quad\text{en supposant que }~ v'=v+\varepsilon\]

On sait que : \[L(v'^2)=L(v^2)+\frac{d}{dt}\big[f(x,~t\big]\]

est un bon lagrangien :

\[\begin{aligned} v'^2&=v^2+2~v~\varepsilon+\varepsilon^2\\ L(v'^2)&=L(v^2)+2~v~\varepsilon~\frac{\partial L}{\partial v^2}+\cdots\end{aligned}\]

On pourra poser : \[2~v~\varepsilon~\frac{\partial L}{\partial v^2}=\frac{d}{dt}\big[f(x,~t)\big]\]

Or : \[v=\frac{dx}{dt}=\varphi(t)\]

Pour que l’identité soit explicitement vérifiée, il faut donc que le terme non dépendant de \(t\) soit une constante : \[\frac{\partial L}{\partial v^2}=cte\quad\Rightarrow\quad L=a~v^2\]

Dans le cas où \(a=m/2\), on retrouve l’énergie cinétique classique \(m~v^2/2\).

Remarque

Examinons l’action pour un point matériel : \[S=\int_{t_1}^{t_2}\frac{(m~v^2)~dt}{2}=\int_{t_1}^{t_2}\frac{m~v}{2}~\frac{ds}{dt}~dt=\int_{s_1}^{s_2}\frac{m~v~dt}{2}\]

Si la masse est constante : \[S=\int_{l_1}^{l_2}v~dl\]

4.2. Lagrangien d’un système de points sans action extérieure

On introduit dans le lagrangien une fonction d’interaction \(U(\overrightarrow{r_1},~\overrightarrow{r_2},~\dots,~\overrightarrow{r_n})\). On peut toujours supposer cette fonction indépendante du temps et postuler que : \[L=\sum_{a=1}^n\frac{m_a~\overrightarrow v_a^2}{2}-U(\overrightarrow{r_1},~\overrightarrow{r_2},~\dots,~\overrightarrow{r_n})\]

Dans une transformation de Galilée, \(U\) est invariant, car les \(r_i\) le sont : \[\frac{d}{dt}\Big(\frac{\partial L}{\partial\overrightarrow{v_a}}\Big)-\frac{\partial L}{\partial\overrightarrow{r_a}}=0\]

On admet que \(m\) est une constante. Il s’ensuit que : \[\frac{\partial L}{\partial\overrightarrow{v_a}}=m_a~\overrightarrow{v_a}\qquad;\qquad \frac{\partial L}{\partial\overrightarrow{r_a}}=-\frac{\partial U}{\partial\overrightarrow{r_a}}\]

D’où la fonction : \[\frac{d(m_a~\overrightarrow{v_a})}{dt}=-\frac{\partial U}{\partial\overrightarrow{r_a}}\]

Comme la masse est une constante, on retrouve le principe fondamental de la dynamique : \[m_a~\overrightarrow{\gamma_a}=-\frac{\partial U}{\partial\overrightarrow{r_a}}=\overrightarrow{f_a}\]

Supposons maintenant que \(x_a=\varphi_a(q_1,~q_2,~\dots,~q_n)\). On a :

\[\begin{aligned} &\dot{x_a}=\frac{dx_a}{dt}=\frac{\partial\varphi_a}{\partial q^i}~\frac{dq^i}{dt}=\dot{q}^i~\frac{\partial\varphi_a}{\partial q^i}\\ &L=\sum a_{ij}~\dot{q}^i~\dot{q}^j-U(q^1,~q^2,~\dots,~q^n)=T-U\quad;\quad a_{ij}= fonction(q^j)\end{aligned}\]

\(T\) représente l’énergie cinétique et \(U\) représente l’énergie potentielle : \[\frac{d}{dt}\Big(\frac{\partial T}{\partial\dot{q}^i}\Big)-\frac{\partial(T-U)}{\partial q^i}=0\]

Soit finalement : \[\frac{d}{dt}\Big(\frac{\partial T}{\partial\dot{q}^i}\Big)-\frac{\partial T}{\partial q^i}=-\frac{\partial U}{\partial q^i}\]

4.3. Système non fermé

Un système \(A\) est non fermé quand il est enfermé par un système \(B\).

Le système \(B\) est le champ dans lequel \(A\) est plongé. Exemple : le pendule \(A\) dans le champ de pesanteur \(B\) : \[L=T_A(q_A,~\dot{q}_A)+T_B(q_B,~\dot{q}_B)-U(q_A,~q_B)\]

\(B\) est considéré comme connu, donc \(q_B(t)\) aussi, donc pareillement \(T_B(t)\) qui doit être la dérivée d’une autre fonction connue du temps ; or, on sait que : \[L'=L+\frac{df}{dt}\quad\text{est un bon lagrangien.}\]

Le terme \(T_B\) devient superflu et on peut garder : \[L=T_A(q_A,~\dot{q}_A)-U\big[q_A(t),~q_B(t)\big]\]

C’est le lagrangien du système \(A\) dans le champ extérieur \(B\) connu. \(U\) est l’énergie potentielle de \(A\) par rapport au champ extérieur.

On peut alors écrire :

\[\begin{aligned} &L=\sum m_a~\frac{\overrightarrow{v_a}^2}{2}-U(\overrightarrow{r_1},~\overrightarrow{r_2},~\dots,~\overrightarrow{r_n},~t)\\ &\frac{d}{dt}\Big(\frac{\partial L}{\partial\dot{q}^i}\Big)-\frac{\partial L}{\partial q^i}=0\end{aligned}\]

Ou encore : \[\frac{d}{dt}\Big(\frac{\partial T}{\partial\dot{q}^i}\Big)-\frac{\partial T}{\partial q^i}=-\frac{\partial U}{\partial q^i}\]