1. Épreuves et fréquences

Pile ou face ? On a une chance sur deux d’obtenir pile (ou face a contrario). Affirmation de bon sens, mais un peu rapide. Est-on sûr, en effectuant 10 lancers de la même pièce, de retrouver le résultat 5 fois pile et 5 fois face, ou même, avec 50 lancers 25 fois pile et 25 fois face ? Effectuons cette expérience un nombre \(N\) de fois de plus en plus grand en notant à chaque fois les résultats obtenus. Chaque lancer est une épreuve.

Si, au cours de ces \(N\) parties, nous avons obtenu le résultat pile \(k\) fois, donc le résultat face \((N-k)\) fois, nous dirons que \(k\) est la fréquence absolue d’apparition de pile en \(N\) parties et \(f=k/N\) sa fréquence relative. Les apparitions des résultats (pile, face) sont appelés événements.

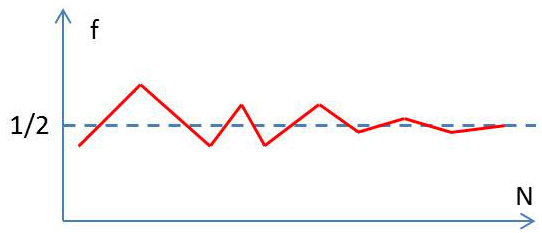Le graphe \(f(N)\) de l’ensemble des résultats en fonction de \(N\) est une ligne brisée, répartie de manière chaotique de part et d’autre de la ligne en pointillée d’ordonnée \(1/2\).

Lorsque le nombre d’épreuves devient très grand, on voit que \(f\rightarrow 1/2\). La ligne brisée tend à se rapprocher de la droite d’ordonnée \(1/2\) qui présente les caractéristiques d’une loi physique.

Une expérience avec un dé à jouer aurait donné la valeur moyenne \(1/6\) pour la fréquence d’apparition de l’une des six valeurs [1, 2, 3, 4, 5, 6].

Ces deux expériences, simples, montrent l’importance qui devra être accordée à la plus grande valeur possible de \(N\), le nombre d’épreuves, de façon à conclure à la convergence de la courbe brisée vers une valeur limite.

Le but du calcul des probabilités et des statistiques est d’étudier des phénomènes analogues dans lesquels ces lois se manifestent, de les enregistrer, de les expliquer, de les prévoir et de les utiliser.

2. Notion de probabilité

Une nouvelle expérience. Nous considèrerons une urne remplie de boules identiques au toucher, mais de couleurs différentes : \(n_1\) bleues, \(n_2\) rouges, \(n_3\) bleues, etc. Le nombre total de boules étant : \[n=n_1+n_2+n_3+ \dots\]

L’épreuve consiste à tirer une boule au hasard, sans la voir, à noter sa couleur et à la remettre dans l’urne. Après un grand nombre \(N\) d’épreuves, on a obtenu les résultats suivants : \(k_1\) boules blanches, \(k_2\) boules rouges, \(k_3\) boules bleues, etc.

Considérons à présent les nombres : \[f_i=\frac{k_i}{N} \quad ; \quad p_i=\frac{n_i}{n}\]

L’expérience montre que, pour \(N\) très grand ces deux nombres se rapprochent.
Les premiers \(f_i\) sont des nombres a posteriori. Les nombres \(p_i\) qui permettent de prévoir les nombres \(f_i\) sont des nombres a priori. On les appelle probabilités pour que les événement \(i\) respectifs se produisent.

En toute rigueur, il faudrait écrire : \[\left\{\frac{k_i}{N}-\frac{n_i}{n}\rightarrow 0\right\}_{N\rightarrow \infty} \quad\text{c'est-à-dire :}\quad \big\{f_i-p_i\rightarrow 0\big\}_{N\rightarrow \infty}\]

Le fait que la proposition est d’autant plus valable que \(N\) est très grand constitue ce que l’on appelle la loi des grands nombres.

3. Événements et probabilité

L’événement aléatoire \(E_i\) (tirage d’une boule) peut se produire de plusieurs façons :

• \(E_i\) : \(\qquad\quad\) tirage d’une boule de la couleur \(i\) ;

• \(p_i=n_i/n\) : probabilité de réalisation de \(E_i\).

 
Il est évident que, \(\forall i\) :

\[\left\{ \begin{aligned} p_i &\geq 0\\ \sum p_i &=\frac{n_1}{n}+\frac{n_2}{n}+ \dots =\frac{n_1+n_2+ \dots}{n}=1 \end{aligned} \right.\]

Il s’agit de l’axiome des probabilités totales.

Nous dirons que :

• Un événement certain \(\qquad\)   a pour probabilité   \(p=1\)

• Un événement impossible \(\quad\) a pour probabilité   \(p=0\)

• Un événement très probable   a une probabilité   proche de \(1\)

• Un événement peu probable   a une probabilité   proche de \(0\)