1. Définition.Tableau de répartition
On considère un ensemble de réels \(\{x_1,~x_2,\cdots,~x_n\}\) auquel on associe les probabilités \(\{p_1,~p_2,\cdots,~p_n\}\) telles que : \[0\leq p_i\leq 1 \quad ; \quad \sum_ip_i=1\]
\[\text{On dit que le système } \left\{ \begin{aligned} x_1\quad x_2\quad x_3\quad\cdots\quad x_n\\ p_1\quad p_2\quad p_3\quad\cdots\quad p_n \end{aligned} \right\} \text{ définit une variable aléatoire } X.\]
Cette variable \(X\) est susceptible de prendre la valeur \(x_i\) avec la probabilité associée \(p_i\). Le tableau précédent est appelé tableau de répartition.
Exemple du lancer de dé : \[\begin{Bmatrix} 1&2&3&4&5&6\\ 1/6&1/6&1/6&1/6&1/6&1/6 \end{Bmatrix}\]
Exemple du jeu de pile ou face (comportement binaire) : \[\begin{Bmatrix} 1&0\\ 1/2&1/2\\ \end{Bmatrix}\]
2. Fonction de répartition
\(X\) étant une valeur courante de \(x\), la fonction de répartition \(F(x)\) est définie par : \[F(x)=Pr(X<x) \qquad \text{Exemple :} \quad F(2)=Pr(X<2)\]
2.1. Propriétés
La fonction de répartition est la caractéristique la plus universelle d’une variable aléatoire. On en retiendra essentiellement quatre propriétés :
\[\begin{aligned} &x_2>x_1 \quad~~~ \text{alors } F(x_2)>F(x_1) \qquad F(x) \text{ fonction non décroissante}\\ &x\rightarrow +\infty \quad~ \text{alors } F(x)\rightarrow 1\\ &x\rightarrow -\infty \quad~ \text{alors } F(x)\rightarrow 0\\ &Pr(x_1\leq x\leq x_2)=F(x_2)-F(x_1)\end{aligned}\]
Discussion
La démonstration est intuitive en imaginant les points \(x\) sur leur axe :
La proposition \(X<x\) revient à situer le point représentatif de \(X\) à gauche du point représentatif de \(x\). Plus on déplace ce point à droite, plus l’espace offert à gauche pour \(F(x)=Pr(X<x)\) est important. Les valeurs limites s’en déduisent facilement.
En faisant \(x\rightarrow +\infty\) on accroît l’intervalle dans lequel \(X\) va se situer. À la limite, cet intervalle offert devenant infini, la probabilité pour que \(X\) appartienne à cet intervalle tend vers la certitude, donc de valeur \(F(x)=1\) qui est en fait la somme des probabilités.
C’est le contraire lorsque \(x\rightarrow -\infty\).
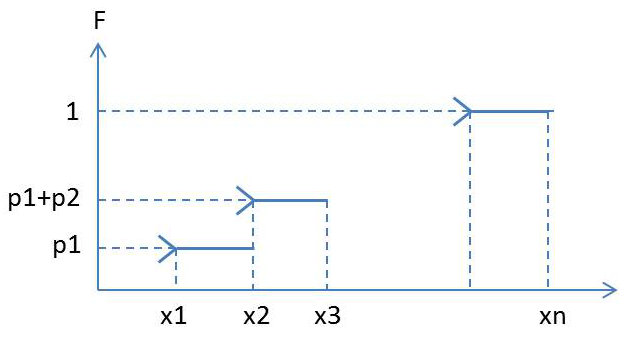
La fonction \(F\) est une fonction cumulative, ce qui se comprend facilement en observant la graphe ci-dessus. On notera que l’extrémité gauche des segments est ouverte, ce qui signifie que la valeur exacte de l’abscisse correspondante est exclue.
Plus généralement : \[F(x_i)=Pr(X<x_i)=p_1+p_2+ \cdots +p_{i-1}\]
Prenons l’exemple du lancer de dé pour fixer les idées :
\[\begin{aligned} &F(1)=Pr(X<1)=0\\ &F(2)=Pr(X<2)=Pr(X=1)=1/6\\ &F(3)=Pr(X<3)=Pr(X=1)+Pr(X=2)=2/6=1/3\\ &\cdots\end{aligned}\]
3. Quelques remarques
Remarque 1
On peut être amené à rencontrer la notation : \[F(x)=Pr(X\leq x)\] Il s’agit en fait de la convention anglo-saxonne. Dans ce cas, la discontinuité dans le graphe de la fonction de répartition est située de manière inverse. Dans ce qui suit, nous conviendrons toujours de la première notation.
Remarque 2
Simple remarque de calcul. Il est intéressant de noter que :
\[\begin{aligned} Pr(X\geq x_i)&=1-Pr(X<x_i)=1-F(x_i)\\ Pr(X>x_i)&=1-Pr(X\leq x_i)=1-Pr(X<x_i)-Pr(X=x_i)\\ &=1-F(x_{i+1})\end{aligned}\]
Remarque 3
Bien noter l’importance du signe \(=\) dans la manipulation des inégalités, les variables étant discrètes. Ce signe perdra son sens dans le cas des variables continues.
