1. Position du problème
Une variable aléatoire \(X\) est définie par sa loi de probabilité : ensemble des pondérations \(p_i\) dans le cas d’une variable continue ou densité de probabilité \(f(x)\) dans le cas d’une variable continue. On sait calculer la moyenne d’une fonction de \(X\) que nous appellerons \(g(X)\), c’est-à-dire, respectivement :
\[\begin{aligned} E\big\{g(X)\big\}&=\sum_iE\big\{g(x_i)\big\} \\ E\big\{g(X)\big\}&=\int_{D_x}g(x)~f_x(x)~dx \qquad D_x~:\text{ domaine de variation de } x\end{aligned}\]
On peut être conduit à créer une nouvelle variable \(Y=g(X)\) et à devoir connaître par exemple l’espérance mathématique \(E(y)\) dans son domaine propre \(D_y\).
On adopte pour le calcul la même expression que pour la variable X. Par exemple, dans le cas continu, on écrira : \[E(Y)=\int_{D_y}g(y)~f_y(y)~dy \qquad D_y~:\text{ domaine de variation de } y\]
Tout le problème est de savoir comment s’effectue la transformation de la densité de probabilité \(f_x(x) ~ \rightarrow ~ f_y(y) \).
2. Méthode de calcul
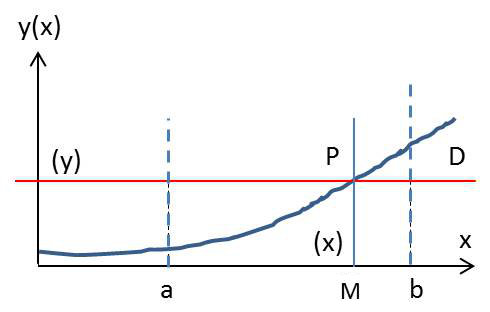Dans un premier temps, on supposera, pour fixer les idées, que \(y=g(x)\) est une fonction monotone croissante.
Au point \(M(x)\), on associe \(P(y)\).
Pour connaître la densité de probabilité \(f_y(y)\) associée à la variable \(y\) on procèdera en deux temps :
1) Détermination l’expression de la fonction de répartition ;
2) Calcul de sa dérivée suivant la nouvelle variable \(y\).
On sait que : \[F(y)=Pr(Y<y)=Pr(a<X<x)=\int_a^xf_x(x)~dx\]
On procède ensuite à ce que l’on appelle la dérivation sous le signe \(\int\).
Rappel : dérivation sous \(\int\)
Nous rappellerons d’abord la technique (formule) de dérivation dans le cas le plus général pour lequel les bornes d’intégration sont fonction de la variable de dérivation, sachant que le cas qui nous intéresse se présente plus simplement, ce qui facilite le calcul.
Considérons l’intégrale : \[I(x)=\int_{a(x)}^{b(x)}f(x,t)~dt\] La formule de dérivation comporte deux termes relatifs aux bornes d’intégration et un terme relatif à la partie intégrable : \[I'(x)=f\big\{x,b(x)\big\}~b'(x)\ - \ f\big\{x,a(x)\big\}~a'(x)\ + \ \int_{a(x)}^{b(x)}\frac{\partial f}{\partial x}(x,t)~dt\]
Utilisons la fonction inverse de \(g(x)\) : \[y=g(x) \quad \rightarrow \quad g^{-1}(x)=\Psi(y)\]
On obtient pour la dérivée : \[f_y(y)=\frac{dF(y)}{dy}=\frac{d}{dy}\left\{\int_a^{\Psi(y)}f_x(x)~dx\right\}=f_x~\Psi(y)~\Psi'(y)\]
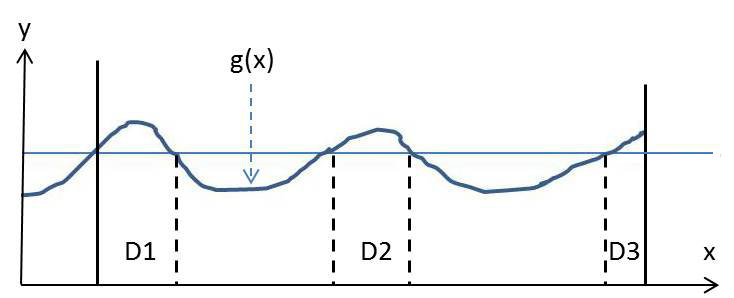Le résultat peut être étendu sans difficulté au cas d’une fonction non monotone : \[F(y)=Pr(Y<y)=\sum_i\int_{D_i}f_x(x)~dx\]
Deux formes simples sont intéressantes :
Forme 1 : \(a\) et \(b\) indépendantes de \(x\) \[\frac{d}{dx}\int_a^bf(x,t)~dt=\int_a^b\frac{\partial f(x,t)}{\partial x}~dt\]
Forme 2 : \[\frac{d}{dx}\left\{\int_a^bf(t)~dt\right\}=f(x)\]
3. Applications du changement de variable
3.1. Exemple 1
Une variable aléatoire \(X\) définie sur un intervalle de longueur \(L\) a une densité de probabilité uniforme. Quelle est la loi de probabilité de \(Y=\ln(X)\) ?
Réponse
Distribution uniforme : \[f_x(x)=\frac{1}{L}\]
Fonction inverse : \[y=\ln(x) \quad \rightarrow \quad x=e^y\]
Relation probabilité - fonction de répartition : \[Pr(Y<y)=Pr(ln(x)<a)=Pr(X<e^y)=F_y(y)=F_x(e^y)\]
Expression de la fonction de répartition : \[F_y(y)=Pr(X<e^y)=\int_0^{e^y}\frac{1}{L}~dx=\frac{e^y}{L}\]
Densité de probabilité (dérivation) : \[f_y(y)=\frac{dF_y}{dy}=\frac{d}{dy}\left(\frac{e^y}{L}\right)=\frac{e^y}{L}\]
3.2. Exemple 2
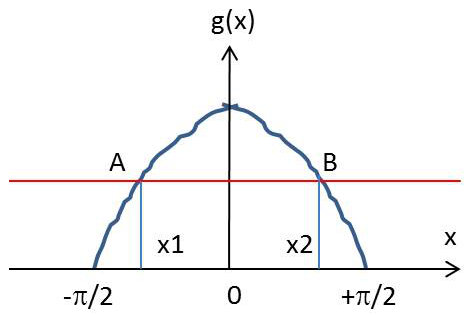On suppose que la variable aléatoire \(X\) est équi-répartie sur l’intervalle \([-\pi/2;+\pi/2\)]. On cherche la loi de répartition de la variable \(Y=\cos(X)\).
Réponse
Répartition uniforme donc densité : \[f_x=\frac{1}{\pi}\]
Fonction de répartition : \[F(y)=\int_{-\pi/2}^{x_1}f_x(x)~dx+\int_{x_2}^{+\pi/2}f_x(x)~dx\]
C’est-à-dire : \[F(y)=\frac{1}{\pi}\int_{-\pi/2}^{-\arccos(y)}dx+\frac{1}{\pi}\int_{+\arccos(y)}^{+\pi/2}dx\]
Densité de probabilité par dérivation : \[f_y(y)=\frac{dF}{dy}=\frac{1}{\pi}\frac{1}{\sqrt{1-y^2}}+\frac{1}{\pi}\frac{1}{\sqrt{1-y^2}}\]
En définitive : \[f_y(y)= \left\{ \begin{aligned} &\frac{2}{\pi}\frac{1}{\sqrt{1-y^2}} \qquad && y\in [0,1]\\ &0 && \text{ailleurs} \end{aligned} \right.\]
