1. Introduction
Un système est susceptible de se trouver dans plusieurs états \(E_i\{i=1,~2,~\dots,~n\}\). On dit qu’il s’agit d’un système à \(n\) états. On suppose de plus que les changements d’état ne peuvent se produire qu’à des instants déterminés \([0,~1,~2,~\dots]\) appelés dates.
À chaque état est associé la probabilité \(p_n(t)\) que le système se trouve dans l’état \(E_n\) à l’instant \(t\). L’ensemble des probabilités correspondant à une date \(t\) donnée est un vecteur (de dimensions égales au nombre d’états possibles) appelé vecteur d’état du système ou encore son vecteur stochastique : \[p(t)=\{p_1(t),~p_2(t),~\dots,~p_n(t)\}\]
Avec les conditions classiques : \[p_i(t)\geq 0 \quad i=1,~2,~\dots,~n \quad \text{et}\quad \sum_{i=1}^{i=n}p_i(t)=1 \quad t=0,~1,~2,~\dots\]
On suppose ici que le passage d’un état \(E_i\) à un autre état \(E_j\), appelé encore transition de \(E_i\) vers \(E_j\), ne dépend que de ces deux états. Cela signifie, de manière simplifiée, que la prédiction du futur, sachant le présent, n’est pas rendue plus précise par des éléments d’information supplémentaires concernant le passé ; toute l’information utile pour la prédiction du futur est contenue dans l’état présent d’un tel processus, dit processus de Markov.
On associe à ces états une probabilité conditionnelle, c’est-à-dire la probabilité pour que le système soit dans l’état \(E_j\) à la date \((t+1)\) sachant qu’il se trouvait dans l’état \(E_i\) à la date \((t)\).
On admet en outre que les probabilités initiales \(\{p_i(0):i=1,~2,~\dots,~n\}\) sont connues.
On obtient ainsi une chaîne de Markov caractérisée par sa matrice de transition \(T=(p_{ij})\) appelée encore matrice stochastique ou matrice de Markov. Ses éléments sont les probabilités de transition d’un état donné à un autre état : \[[p(t+1)]=[p(t)]\times[T] \quad \text{et}\quad [T]=[p_{ij}]\]
Avec : \[p_{ij}\geq 0 \quad i,j=1,~2,~\dots,~n \quad \text{et}\quad \sum_{j=1}^{n} p_{ij}=1 \quad i=1,2,...,n\]
On notera l’ordre dans lequel se fait la multiplication : Vecteur – Matrice.
Si ces éléments sont fonction du temps, alors la chaîne de Markov est non stationnaire. Nous n’étudierons ici que les processus stationnaires.
2. Représentations de la chaîne de Markov
 Il existe deux modes de représentation : la représentation par graphe et la représentation par tableau ou matrice.
Il existe deux modes de représentation : la représentation par graphe et la représentation par tableau ou matrice.
Nous en donnons un exemple : \[\begin{matrix} &|&E1&E2&E3\\ \hline E1&|&0.2&0&0.8\\ E2&|&0.3&0.4&0.3\\ E3&|&0.5&0.5&0 \end{matrix}\]
3. Construction de la matrice
Pour fixer les idées sans que cela nuise à la généralité des explications, nous raisonnerons sur deux exemples très simples.
Exemple 1
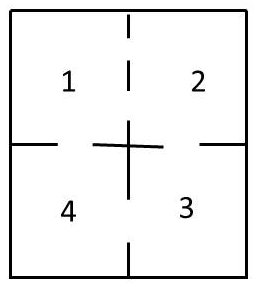 Le diagramme ci-contre représente un ensemble de quatre compartiments. Des portes permettent de passer d’un compartiment à l’autre. Une souris, placée dans un compartiment quelconque, aura la même probabilité de passer par n’importe laquelle de ce compartiment. Il s’agit de déterminer la matrice de transition de cette chaîne d’un système à quatre états.
Le diagramme ci-contre représente un ensemble de quatre compartiments. Des portes permettent de passer d’un compartiment à l’autre. Une souris, placée dans un compartiment quelconque, aura la même probabilité de passer par n’importe laquelle de ce compartiment. Il s’agit de déterminer la matrice de transition de cette chaîne d’un système à quatre états.
On suppose que la souris ne peut pas rester dans un même compartiment d’un instant \(t\) à un instant immédiatement suivant \((t + 1)\). La probabilité de passage d’un compartiment à l’autre est naturellement liée au nombre de portes permettant ce passage, l’animal empruntant l’une des ouvertures qui se présentent.
On aura donc la matrice de transition suivante : \[\begin{matrix} &|&E1&E2&E3&E4\\ \hline E1&|&0&2/3&0&1/3\\ E2&|&2/3&0&1/3&0\\ E3&|&0&1/2&0&1/2\\ E4&|&1/2&0&1/2&0 \end{matrix}\]
On notera que la somme des éléments d’une ligne donnée est égale à 1.
Exemple 2
Une personne se rend chaque jour à son travail, soit en voiture, soit en train. Elle ne prend jamais le train deux fois de suite. Quand elle s’est rendue un jour à son travail, elle peut, le jour suivant, prendre le train comme reprendre la voiture.
On a donc les transitions suivantes : \[T/T=0 \qquad T/V=1 \qquad V/T=V/V=1/2\]
D’où la matrice stochastique : \[\begin{matrix} &|&0&T&V\\ \hline T&|&0&1\\ V&|&1/2&1/2 \end{matrix} \qquad \text{c'est-à-dire :}\quad [T]= \begin{pmatrix} 0&1\\ 1/2&1/2 \end{pmatrix}\]
4. Transitions d’ordre supérieur
Le problème se pose de la manière suivante. L’élément de la matrice de Markov est la probabilité pour que \(E_i\rightarrow E_j\) en une transition. Quelle est la probabilité pour que le système effectue cette évolution en n transitions exactement ?
Autrement dit : \[E_i\rightarrow \{E_{k_1} \rightarrow E_{k_2}\rightarrow .....\rightarrow E_{k_{n-1}}\}\rightarrow E_j\]
Il existe deux méthodes pour y parvenir, la première étant une méthodes dite pas à pas : \[[p^{1}]=[p^{(0)}]\times[T] ......... [p^(n)]=[p]^{(n-1)}\times[T]=[p^{(0)}]\times{[T]}^n\]
\(p^{(0)}\) est un vecteur de probabilité d’état initial, c’est-à-dire avant la première application de la matrice \([T]\).
\({[T]}^n\) est donc la matrice de transition depuis un état initial et après exactement de \(n\) transitions.
Exemple
On peut imaginer que notre voyageur va jouer au dé son choix de départ, par exemple en décidant de partir la première fois en voiture s’il obtient au jet du dé un 2 ou un 4. Cela signifie qu’il y a 1 chance sur 3 de prendre la voiture le premier jour. le vecteur d’état correspondant sera donc \(p^{(0)}=[2/3,1/3]\).
Donc, à la quatrième transition : \[p^{(4)}=p^{(0)}\times{[T]}^4)=[2/3,1/3]\times \begin{pmatrix} 3/8&5/8\\ 5/16&11/16 \end{pmatrix} = (17/48,31/48)\]
Ainsi, à la quatrième transition, il y 31 chances sur 48 que le voyageur prenne sa voiture.
5. Matrice régulière
Une matrice stochastique est dite régulière s’il existe une puissance de cette matrice où tous ses éléments sont strictement positifs. C’est le cas de la matrice \([T]\) de l’exemple précédent puisque \([T]^2\) répond aux critères : \[[T]=\begin{pmatrix} 0&1\\ 1/2&1/2 \end{pmatrix} \qquad {[T]}^2= \begin{pmatrix} 1/2&1/2\\ 1/4&3/4 \end{pmatrix}\]
Il est intéressant de voir l’évolution de la matrice avec le temps. Dans l’exemple précédent, on peut avoir une idée de ce que seront les probabilités pour notre voyageur au quatrième jour : \[{[T]}^4= \begin{pmatrix} 3/8&5/8\\ 3/16&11/16 \end{pmatrix}\]
On notera que la somme des éléments d’une ligne donnée a pour valeur 1.
6. Vecteur fixe et point fixe
6.1. Théorème (énoncé sans démonstration)
La matrice régulière \([T]\) contient un vecteur stochastique constant \(\Theta\) et un seul dont les composantes sont toutes positives.
La suite \(T,~T^2, T^3 . . . \) des puissances de \([T]\) converge vers la matrice \([T_f]\) dont les lignes sont toutes le vecteur \(\Theta\).
Si \([p]\) est un vecteur stochastique quelconque, la suite \(pT,~pT^2,~pT^3,~\dots \) converge vers \(\Theta\).
Remarque
Dire que \(T^n\) converge vers \(T_f\) signifie que chaque élément de \(T^n\) converge vers l’élément correspondant de \(T_f\).
Dire que \(pT^n\) converge vers \(\Theta\) signifie que chaque composante de \(pT^n\) converge vers la composante correspondante de \(\Theta\).
6.2. Exemple
En toute rigueur, la recherche du vecteur fixe \(\Theta\) est une recherche de vecteur propre. Une astuce permet de s’en dispenser, ce que l’on peut expliquer à travers l’exemple précédent, en remarquant qu’à partir d’une transition donnée, le vecteur d’état se conserve d’un état au suivant immédiat.
Il suffit de résoudre les équations : \[(x,y)\times \begin{pmatrix} 0&1\\ 1/2&1/2 \end{pmatrix} =(x,y) \qquad \text{avec} \quad x+y=1\]
Le calcul donne : \(\Theta=(1/3,2/3)\)
On pourra vérifier que les valeurs de ces composantes sont déjà contenues à partir de la cinquième transition. On peut dire qu’au bout d’un certain temps, le système se stabilise : la personne prend sa voiture avec une fréquence de 2/3 et le train avec une fréquence de 1/3.
7. État absorbant
On dit qu’un état \(E_i\) d’une chaîne de Markov est un état absorbant si le système reste dans cet état une fois qu’il y est entré. Un état \(E_i\) sera absorbant si et seulement si la \(i\)-ième ligne de la matrice de transition \([T]\) porte un un sur sa diagonale principale et des zéros ailleurs.

