1. Uniformité
Une fonction est uniforme en \(M\) si, revenant en \(M\) sur un chemin donné, la fonction reprend la même valeur.
Vérifions cette propriété pour les trois fonctions type : exponentielle, racine et logarithme.
1.1. Fonction exponentielle
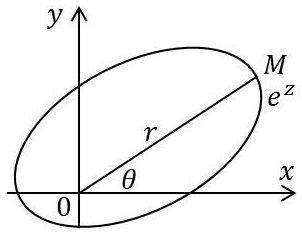La fonction exponentielle est uniforme, car, si on exprime l’affixe sous forme polaire \(z=re^{i~\theta}\), quand le point \(M\) effectue un tour complet sur le chemin dessiné, on a : \[r\rightarrow r\qquad\text{et}\qquad \theta\rightarrow\theta+2~\pi\]
L’affixe \(z\) retrouve le même argument puisque \(e^{2~i~\pi}=1\) (périodicité) et la fonction f(z) retrouve elle aussi exactement la même valeur.
1.2. Fonction racine
Pour vérifier l’uniformité de la fonction racine, nous allons rencontrer cette fois un problème d’argument et d’indétermination suivant le parcours choisi.
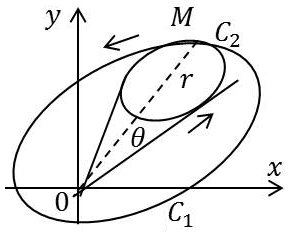Considérons d’abord le parcours \(C_1\). Après un premier tour, l’argument augmentera de \(\pi\). Après un deuxième tour, il aura augmenté de \(2\pi\) pour redonner la valeur initiale.
Il y aura alors deux déterminations, l’une donnant \([z_1]\) et l’autre donnant \([z_2 = - z_1]\). On dit que la fonction est multiforme et que l’origine est un point critique. Il en sera de même pour les fonctions du type \(z^{1/n}\).
Considérons maintenant le parcours \(C_2\). Cette fois, l’argument retrouve sa même valeur et il en est de même de la fonction qui est alors uniforme du fait que le deuxième contour a évité le point critique.
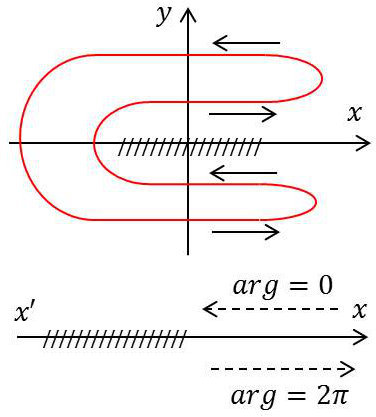Nous verrons par la suite, avec le calcul pratique d’intégrales à variables réelles mais utilisant le prolongement complexe (calcul des résidus) qu’il est important de savoir choisir ce contour.
Toute une partie de l’intégration sur le contour donne un résultat nul et il subsiste l’intégration le long de l’axe des réels. Il faut savoir dans ce cas quel est l’argument correspondant en ayant levé l’indétermination.
Par exemple, au trajet en sens positif correspond l’argument zéro et dans celui en sens négatif l’argument \(2\pi\) qui sera divisé suivant l’ordre de la racine.
1.3. Fonction logarithme
Par définition : \[Z=\ln(z)\qquad\Rightarrow\qquad z=e^Z\]
En coordonnées polaires : \[z=\rho~e^{i~\theta}=e^{X+i~Y}=e^X~e^{i~Y}\]
En identifiant :
\[\begin{aligned} \rho=e^X\qquad&\Rightarrow\qquad X=\ln(\rho)\qquad \rho>0\\ e^{i~\theta}=e^{i~Y}\qquad&\Rightarrow\qquad Y=\theta+2~k~\pi\end{aligned}\]
Par suite : \[Z=\ln(\rho)+i~(\theta+2~k~\pi)\]
Par exemple : \[\ln(-2)=\ln(2~e^{i~\pi})=\ln(2)+i~(\pi+2~k~\pi)\]
Il y a donc une infinité de déterminations.
Pour \(k=0\), la détermination est dite principale. L’origine est donc un point critique pour la fonction \(\ln(z)\).
Les chemins d’intégration de ces fonctions seront déterminés de la même manière que pour les fonctions précédentes.
2. Holomorphie
2.1. Définition
Une fonction est dite holomorphe en un point \(A\) si elle admet une dérivée continue en ce point et si elle y est uniforme. Elle est donc analytique, régulière et uniforme. La définition s’étend à une région.
2.2. Points singuliers
Un point est dit singulier pour \(f(z\)) si cette fonction n’est pas holomorphe en ce point. Ce point est isolé s’il n’en existe pas d’autres dans le voisinage.
Les points singuliers sont classés en deux catégories : points critiques et points non critiques.
Un point est critique lorsque la fonction est non uniforme en ce point. La fonction logarithme et la fonction racine en sont des exemples :
\[\begin{aligned} \ln(z)\quad\text{en}~z=0\qquad&;\qquad \ln(z-a)\quad\text{en}~z=a\\ \sqrt{(z)}\quad\text{en}~z=0\qquad&;\qquad \sqrt{(z-a)}\quad\text{en}~z=a\end{aligned}\]
Un point est non critique lorsque la fonction y est uniforme. Il en existe deux catégories : les pôles et les points essentiels.
En un pôle, la fonction \(f(z)\) est non holomorphe, mais la fonction \(1/f(z)\) l’est. Par exemple : \[f(z)=\frac{P(z)}{(z-a)^2~(z-b)}\qquad\text{avec :}\quad P(z)\neq 0\quad\text{pour}\quad z=(a,b)\]
\(z=a\) est un pôle double ; \(z=b\) est un pôle simple.
Une fonction qui ne possède pas de pôles est appelée fonction méromorphe. Par exemple : \[f(z)=e^{1/z}\quad\text{pour}\quad z=0\]
On peut cependant vérifier que cette fonction est uniforme.
3. Contours et bases de calcul en intégration
3.1. Majoration d’intégrale
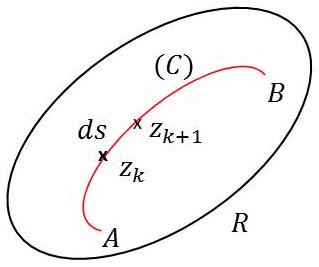On considère la courbe \(C\) rectifiable. On peut donc calculer la somme : \[S=\sum_{k=1}^nf(\zeta_k)~(z_{k+1}-z_k)\quad;\quad \zeta_k\in[z_{k+1},~z_k]\]
À la limite, \(f(z)\) supposée intégrable : \[S\rightarrow I=\int_C f(z)~dz\quad;\quad I\in(C)\]
Si \(L\) désigne la longueur de courbe \(C\) et \(M\) le maximum de \(|f(z)|\), on montre que : \[|I| = \Big|\int_C f(z)~dz\Big|~~\leq~~M\int_C ds = M~L\]
3.2. Lemmes de Jordan
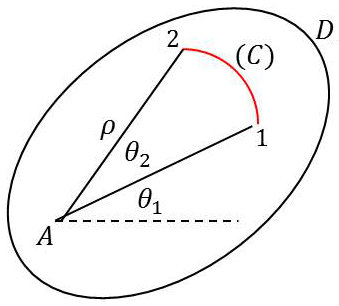On considère, dans un domaine \(D\), l’arc de courbe \(C\) (secteur) de centre \(A\).
On pose : \[\theta_1\leq\theta\leq\theta_2\qquad;\qquad z-a=\rho~e^{i~\theta}\]
On suppose que : \[\lim_{\rho~\rightarrow~\infty}~\sup\big|(z-a)~f(z)\big|=0\]
Alors : \[\lim\int_C f(z)~dz=0\]
Ce cas se produit quand le rayon du secteur devient très grand et tend vers l’infini.
On arrive aux mêmes conclusions quand \(\rho\rightarrow 0\).
L’application de ces deux lemmes permet dans certains cas de constater que l’intégration le long d’un chemin peut donner un résultat nul, ce qui permettra de simplifier les résultats.
3.3. Théorème de Cauchy
Énoncé
Soit une région \(R\) compacte dans laquelle \(f(z)\) est holomorphe. Alors : \[\int_{\Gamma} f(z)~dz=0\]
En effet, orientons la frontière dans le sens trigonométrique positif et posons : \[f(z)=P+i~Q\qquad;\qquad dz=dx+i~dy\]
On a alors :
\[\begin{aligned} &I=\int_{\Gamma} f(z)~dz=\int_{\Gamma}(P+i~Q)~(dx+i~dy)\\ &I=\int_{\Gamma} P~dx-Q~dy+i\int_{\Gamma} Q~dx+P~dy\end{aligned}\]
En appliquant la formule de Riemann (équivalence entre l’intégrale simple sur la bordure et l’intégrale double sur le disque) : \[\iint_R\Big(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\Big)~dx~dy +i\iint_R\Big(\frac{\partial P}{\partial x}-\frac{\partial Q}{\partial y}\Big)~dx~dy\]
En appliquant les conditions de Cauchy : \[P'_x=Q'_y\qquad;\qquad P'_y=-Q'_x\]
On retrouve bien \(I=0\).
Conséquence
Considérons un pôle \(a\) et le circuit dans lequel on a introduit une coupure. Les circuits sont orientés comme indiqué sur la figure.
Dans le circuit qui a contourné le pôle \(a\), la fonction est naturellement holomorphe, d’où : \[\int_{\gamma} f(z)~dz=0\]
Comme les intégrales le long des segments entre les courbes \(C_1\) et \(C_2\) se compensent, il reste : \[\int_{C1} f(z)~dz+\int_{C2} f(z)~dz=0\qquad\Rightarrow\qquad I_{C_1}=-I_{C_2}\]
Ce résultat est très important et fait apparaître l’une des premières astuces de calcul dans ce domaine en remplaçant le calcul sur le contour \(C_2\) par le calcul sur le contour \(C_1\) auquel on peut donner une forme géométrique particulièrement intéressante du moment qu’elle entoure le pôle (un cercle par exemple).
Contre-exemple intéressant
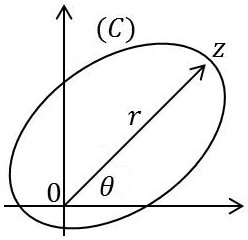Considérons la fonction : \[f(z)=\frac{1}{z}\]
et l’intégrale correspondante : \[I=\int_C f(z)~dz\]
Au point \(O\), la fonction \(f(z)\) est non holomorphe, donc \(I\) devra être non nulle. En effet : \[I=\int_C\frac{dz}{z}\]
Effectuant le changement de variable : \(z=\rho~e^{i~\theta}\) :
\[\begin{aligned} &I=\int_C (d\rho~e^{i~\theta}+\rho~i~e^{i~\theta}~d\theta)~\frac{1}{\rho~e^{i~\theta}}\\ &I=\int_C \frac{d\rho}{\rho}+i\int_C d\theta\end{aligned}\]
C’est-à-dire : \[I=\big[\ln~\rho\big]_{\rho 1}^{\rho 2}+2~i~\pi=2~i~\pi\]
Donc, quel que soit le contour autour de l’origine, on retrouve toujours le résultat qui est une sorte de période pour chaque tour autour de \(O\).
4. Primitive d’une fonction holomorphe
En reprenant des calculs analogues à ceux effectués au paragraphe précédent et en reconsidérant le circuit dans lequel le contour \(C_2\) est un cercle dans lequel on fait tendre le rayon vers 0, on obtient alors un résultat remarquable dit formule de Cauchy : \[f(a)=\frac{1}{2~i~\pi}~\int_{C1}\frac{f(z)~dz}{z-a}\]
Il suffit pour cela de considérer que la fonction \(f(z)\) est holomorphe et que la fonction \(\cfrac{f(z)}{z-a} \) est holomorphe. Il s’ensuit le résultat remarquable suivant : \[I=\int_{C1}\frac{f(z)}{z-a}~dz=2~i~\pi~f(a)\]
5. Dérivées successives des fonctions holomorphes
5.1. Formule de Cauchy généralisée
En étudiant la limite quand \(h\rightarrow 0\) de : \[\frac{f(a+h)-f(a)}{h}=\frac{1}{2~i~\pi}~\int_{C1}\frac{f(z)~dz}{(z-a)~(z-a-h)}\]
on peut démontrer que : \[f'(a)=\frac{1}{2~i~\pi}~\int_{C1}\frac{f(z)~dz}{(z-a)^2}\]
Résultat généralisable : \[f^{(n)}(a)=\frac{n!}{2~i~\pi}\int_{C1}\frac{f(z)~dz}{(z-a)^{n+1}}\]
5.2. Théorème du maximum du module
Nous énoncerons ce théorème sans démonstration :
Une fonction holomorphe dans un domaine fermé ne peut avoir son module maximum que sur la frontière de ce domaine, sauf si cette fonction est constante.
5.3. Équation de Laplace
Soit \(f(z)\) une fonction holomorphe. On pose \(f(z)=P+i~Q\).
On suppose que \(f'(z)\) existe, qu’elle est continue et qu’il en est de même pour \(P'\) et \(Q'\). On suppose de plus que ces dernières sont liées par les conditions de Cauchy.
Les dérivées secondes sont aussi continues :
\[\begin{aligned} \frac{\partial P}{\partial x}=\frac{\partial Q}{\partial y}\qquad&;\qquad \frac{\partial P}{\partial y}=-\frac{\partial Q}{\partial x}\\ \frac{\partial^2P}{\partial x^2}=\frac{\partial^2Q}{\partial x~\partial y}\qquad&;\qquad \frac{\partial^2P}{\partial y^2}=-\frac{\partial^2Q}{\partial x~\partial y}\end{aligned}\]
D’où le laplacien : \[\Delta P=\frac{\partial^2P}{\partial x^2}+\frac{\partial^2P}{\partial y^2}=0\]
La fonction \(P\) est donc harmonique et il en est de même pour \(Q\).
Théorème
Si dans un domaine une fonction est holomorphe, alors ses parties réelle et imaginaire sont harmoniques.
Réciproque
Si une fonction \(P(x,~y)\) est harmonique dans un domaine, elle peut être considérée comme la partie réelle d’une fonction holomorphe dans ce domaine.
Exemple
On considère la fonction \(P=x^2-y^2\)
Calculons les dérivées premières et secondes :
\[\begin{aligned} \frac{\partial P}{\partial x}=2~x\quad&;\quad \frac{\partial^2P}{\partial x^2}=2\\ \frac{\partial P}{\partial y}=-2~y\quad&;\quad \frac{\partial^2P}{\partial y^2}=-2\end{aligned}\]
On a bien pour le laplacien : \[\Delta P=\frac{\partial^2P}{\partial x^2}+\frac{\partial^2P}{\partial y^2}=0\]
\(P\) est donc bien une fonction harmonique. C’est la partie réelle d’une fonction analytique.
Recherchons la partie imaginaire \(Q\) en partant des conditions de Cauchy : \[\frac{\partial P}{\partial x}=\frac{\partial Q}{\partial y}\qquad;\qquad \frac{\partial P}{\partial y}=-\frac{\partial Q}{\partial x}\]
On a donc :
\[\begin{aligned} &\frac{\partial Q}{\partial y}=2~x\quad\Rightarrow\quad Q(x,~y)=2~x~y+f(x)\\ &\frac{\partial Q}{\partial x}=2~y+f'(x)=-\frac{\partial P}{\partial y}=2~y\end{aligned}\]
On a donc aussi : \[f'(x)=0\quad\Rightarrow\quad f(x)=2~x~y+cte\]
Et par suite : \[f(z)=P+i~Q=x^2-y^2+2~x~y+cte=z^2+cte\]
On retrouve un résultat bien connu.
