1. Piles à électrodes différentes

Considérons le cas de piles à électrodes différentes, par exemple en cuivre et en zinc.

On appelle f.é.m. la d.d.p. entre électrodes à vide, c’est-à-dire sans débit de courant.

1.1. Solution à 1 molécule gramme de ($SO_4Zn,~SO_4Cu$) dans 1 litre d’eau

On a les potentiels respectifs : $$\begin{aligned} &C_u/C_u^{2+}~:\qquad &&V_1=V_0+0,340~\rm V~(25~^oC)\\ &Z_n/Z_n^{2+}~: &&V_2=V_0-0,762~\rm V~(25~^oC) \end{aligned}$$

Valeurs déterminées par référence avec une électrode à hydrogène.

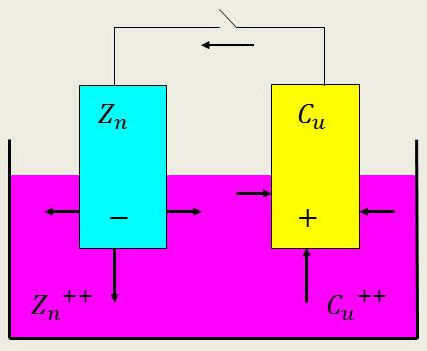L’électrode de cuivre est en principe à un potentiel supérieur de 0,34 V à celui de la solution tandis que l’électrode de $Zn$ est à un potentiel inférieur de 0,76 V à celui de la solution (ceci n’est pas certain, car la solution contient actuellement deux cations).

L’électrode de cuivre serait donc à un potentiel de 1,102 V supérieur à celui de l’électrode de zinc, ce que l’expérience confirme.

En circuit ouvert, le zinc se dissout spontanément et les ions $Cu^{2+}$ se déposent sur l’électrode de cuivre jusqu’à ce que les forces coulombiennes arrêtent cette migration.

En circuit fermé, le courant circule dans le fil dans le sens de la flèche. Si on relie par un fil conducteur les deux électrodes, un courant circule dans ce fil du cuivre [+] au zinc [–].

Dans la solution, le courant va du zinc au cuivre. Il est constitué par un transport d’ions $Zn^{2+}$ et $Cu^{2+}$, car le zinc se dissout spontanément dans la solution et les ions $Cu^{2+}$ se déposent spontanément sur l’électrode de cuivre où ils sont neutralisés par des paires d’électrons.

Au cours du temps, la différence de potentiel diminue, car la concentration en zinc croît et celle en cuivre décroît.

1.2. Pile Daniell

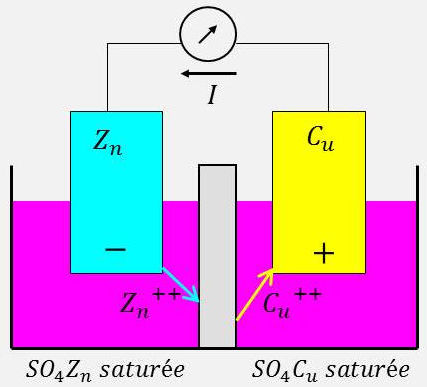Deux solutions maintenues saturées, donc à concentration constante, et reproductible à une température donnée de $SO_4C_u$ sont séparées par une paroi poreuse. Une électrode de zinc plonge dans la première et une électrode de cuivre dans la deuxième.

La f.é.m. est encore 1,10 V et pourtant les concentrations sont différentes.

Il faut tenir compte de la d.d.p. entre les solutions. Globalement, la réaction physicochimique se réduit à : $$SO_4Z_n+C_u\quad\rightarrow\quad SO_4C_u+Z_n+2~W$$ $$\text{cristal}\quad\text{métal}\qquad\quad\text{cristal}\quad\text{métal}\qquad$$

car les solutions sont saturées, avec : $$W=\frac{49,7}{2\times 23}=1,08~\text{eV par charge élémentaire}$$

1.3. Pile Volta

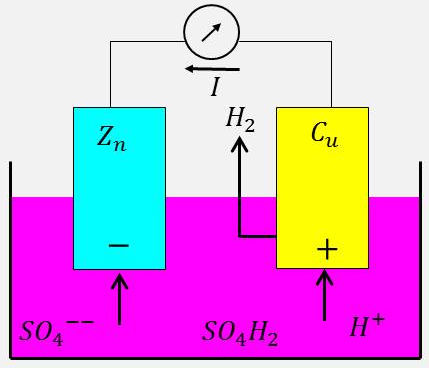Deux électrodes, l’une de zinc, l’autre de cuivre, plongent dans une solution de $SO_4H_2$. Le zinc pur n’est pas attaqué si un fil connecte les deux électrodes, un courant passant du cuivre au zinc, car :

• les ions $SO_4^{2-}$ viennent dissoudre l’électrode de zinc : $$SO_4^{2-}+Zn\quad\rightarrow\quad SO_4^{2-}+Z_n^{2+}+2~e^-$$

• les ions $H^+$ se neutralisent sur le cuivre : $$SO_4^{2-}+2~H^++Z_n\quad\rightarrow\quad SO_4Z_n+H_2^{\uparrow}+2~W$$

avec $W = 0,85~\rm eV$ par charge élémentaire.

La f.é.m. à l’origine est effectivement de 0,85 volt, mais elle décroît au cours du temps, car l’hydrogène dégagé et partiellement absorbé, modifie les d.d.p. de contact : l’électrode de cuivre se polarise. On évite en général la polarisation par dégagement d’hydrogène en plaçant l’électrode positive dans un milieu oxydant comme $M_nO_2$.

Remarques

Un tel phénomène ne se produit pas avec la pile Daniell qui est réversible et n’est pas polarisable, car aucune réaction secondaire ne se produit sur les électrodes.

La pile Volta n’est pas réversible : le passage du courant dans le sens inverse provoque la dissolution du cuivre dans $SO_4H_2$ : $$SO_4H_2+C_u~~\rightarrow~~SO_4C_u+H_2^\uparrow$$

2. Pile de concentration

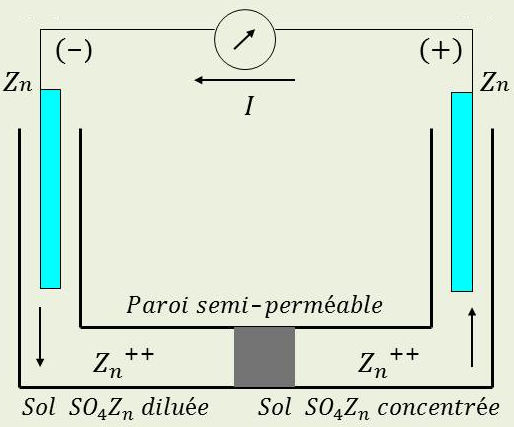Considérons le schéma de la figure ci-contre où les concentrations en $SO_4Zn$ sont inégales ($C_1 > C_2$).

Un tel système est partiellement ordonné ; on sait qu’il tend vers le désordre avec l’aide de l’agitation thermique. Il en résulte une d.d.p. entre électrodes.

On constate que les deux solutions sont au même potentiel et on montre que la d.d.p. entre les deux électrodes est : $$E=\frac{0,58}{Z}~\{\log_{10}(C_1)-\log_{10}(C_2)\}$$

C’est-à-dire : $$E=\frac{0,58}{Z}~\log_{10}\frac{C_1}{C_2}$$

Ici, $n=2$ et l’électrode positive est celle qui plonge dans la solution concentrée où les ions $Z^{2+}$ viennent se décharger conformément à la réaction : $$Zn^{2+}\quad\rightarrow\quad Zn-2~e^-$$

Cette électrode devient positive parce que des électrons lui sont enlevés.

Un cas particulier est celui de deux électrodes à hydrogène : $$E=0,058~\log_{10}\frac{[H^+]_1}{[H^+]_2}=0,058~(pH_2-pH_1)$$

On rappelle que : $$pH=-\log_{10}[H^+]$$

On peut également mesurer le pH à l’aide d’une seule électrode à hydrogène et d’une électrode de référence (par exemple l’électrode au calomel qui est remarquablement stable et reproductible quoique polarisable).

La d.d.p. est donnée en fonction du pH par une formule du type : $$E=E_0+0,058~pH$$

3. Accumulateurs

Deux électrodes de plomb oxydées en milieu sulfurique concentré se polarisent fortement si on fait passer le courant dans l’acide, d’une électrode dont la borne est conventionnellement marquée (+) ou colorée en rouge à l’autre électrode marquée (–) ou colorée en noir. Au cours de cette polarisation, les ions acquièrent une énergie potentielle voisine de 2 eV par charge élémentaire en formant différents oxydes complexes.

Il se trouve que si, après le traitement de charge, on connecte les bornes par un fil conducteur, l’accumulateur se décharge. Un courant passe alors dans le fil de la borne (+) à la borne (–).

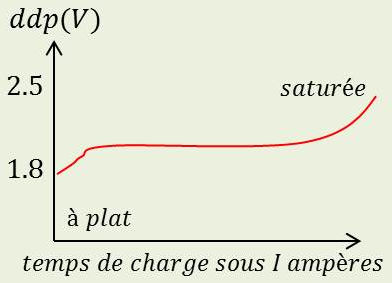Un accumulateur est caractérisé par sa courbe de charge et de décharge. On en déduit :

1. La d.d.p. entre électrodes en régime normal (ici $E$ = 2 V).

2. La charge qu’il est capable de débiter dans un circuit. On donne souvent à cette charge le nom de capacité $Q$ que l’on exprime en ampères-heures.

   Un accumulateur de 30 A.h est capable de débiter 1 A pendant 30 heures (ou 0,1 A pendant 300 heures, mais pas 1000 A pendant 0,03 heure).

   On note qu’un tel accumulateur est chargé par une réaction chimique portant sensiblement sur une valence gramme (30 A h=108 000 C, donc voisin de 96 500 coulombs).

3. L’énergie emmagasinée. On aura ici : $$W=Q~E=216~000~\rm J\quad ou\quad W=2\times 30=60~W~h$$

   obtenue en multipliant la f.é.m. par la capacité en A.h.

   Une molécule gramme d’essence fournit en brûlant une énergie comparable, mais la masse d’essence correspondante, récipient compris, n’est que de quelques décigrammes. En comparaison, dans un accumulateur, seule la portion des électrodes voisine de la surface en contact avec l’acide est active ; c’est-à-dire souvent à peine le centième de la masse totale. On sait faire des accumulateurs moins lourds mais plus onéreux.

4. Formule de Helmholtz

Nous avons exprimé la f.é.m. d’une pile en fonction de l’énergie chimique mise en jeu :

$$\begin{aligned} &E=W / e &&\text{énergie chimique par charge élémentaire} \\ &E=Q / \mathcal{F} &&Q~:~\text{énergie dégagée par la réaction chimique} \\ & &&\mathcal{F}~:~\text{le faraday, c'est-à-dire 96 500 coulombs}\end{aligned}$$

Or, les piles fonctionnent généralement d’une manière isotherme en échangeant de l’énergie avec le milieu ambiant.

Une pile qui débite se refroidit généralement et pompe donc la quantité de chaleur $Q$ dans l’atmosphère de sorte que $E > W / e$ : $$E=\frac{Q+Q'}{F}$$

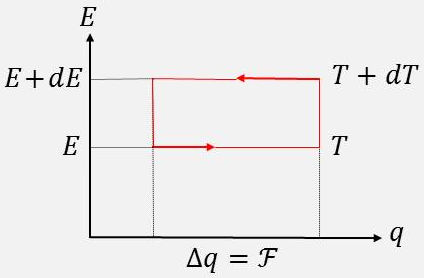Pour les piles réversibles, $Q’$ peut être évaluée en décrivant le cycle ci-contre où la quantité d’électricité est : $$\Delta q=\mathcal{F}$$

• Énergie fournie par la pile : $dE~\Delta q$

• Quantité de chaleur fournie par la source chaude : $Q’$

• Quantité de chaleur reçue par la source froide : $Q''$

Soit : $$\Delta q~dE=\mathcal{F}~dE=Q'-Q''$$

D’après le théorème de Carnot : $$\frac{Q'-Q''}{Q'}=\frac{dT}{T}$$

On a donc : $$\mathcal{F}~dE=Q'~\frac{dT}{T}\qquad\Rightarrow\qquad\frac{Q'}{\mathcal{F}}=\frac{1}{T}~\frac{\partial E}{\partial T}$$

D’où : $$E=\frac{Q}{\mathcal{F}}+T~\frac{\partial E}{\partial T}$$