1. Structure de la matière
On peut considérer la matière comme un agrégat de particules élémentaires : électrons, protons, neutrons, etc. Ces particules sont supposées chargées : le nombre qui mesure cette charge est soit positif, soit négatif.
Un objet matériel est électriquement neutre, car il contient autant de charges positives que de charges négatives. Si, par un procédé quelconque, on enlève de cet objet des charges d’un certain signe (par exemple négatif), alors celui-ci devient porteur d’un excès des charges de signe contraire (ici positif). On dit qu’il est chargé (ici positivement) ou électrisé.
On peut électriser un corps de plusieurs manières. Le procédé le plus élémentaire est le frottement. Prenons l’exemple (souvenir d’école ou de lycée) de la règle en matière plastique frottée vigoureusement avec un chiffon. En approchant cette règle d’un lambeau de buvard, celui-ci est attiré par la règle, suffisamment approchée.
 De manière plus sérieusement scientifique, la règle peut être remplacée par un bâton de verre, le chiffon par une peau de chat et le lambeau de buvard par une boule en moelle de sureau retenue par un fil (pendule).
De manière plus sérieusement scientifique, la règle peut être remplacée par un bâton de verre, le chiffon par une peau de chat et le lambeau de buvard par une boule en moelle de sureau retenue par un fil (pendule).
Mais, pour une catégorie de corps (conducteurs), le plus simple est de les réunir à la borne positive (ou négative) d’un générateur de courant, l’autre borne étant reliée au sol.
Enfin, l’expérience montre que les corps chargés s’attirent ou se repoussent suivant que leurs charges respectives sont de signes contraires ou de même signe.
2. Loi de Coulomb
L’étude des forces qui s’exercent entre particules chargées a été faite par Coulomb dès 1785 au moyen d’un balance de torsion et de petites balles en moelle de sureau. Il a proposé sa fameuse relation (hypothèse de l’expérience dans le vide) : \[F=k\frac{q~q'}{r^2}\quad\text{ou}\quad\overrightarrow{F}=k~\frac{q~q'}{r^2}~\frac{\overrightarrow{r}}{r}\quad;\quad k=\frac{1}{4\pi~\varepsilon_0}\qquad[1]\]
Remarque
En mécanique ondulatoire, la loi de Coulomb s’applique entre électrons, ou entre noyaux et électrons dans les atomes ou molécules. Cependant, la loi de Coulomb ponctuelle ne serait plus valable, au sens stricte, pour des distances de l’ordre de \(10^{-12}\) à \(10^{-13}\) centimètres. La loi de Coulomb dans son essence ne serait pas inexacte, mais on ne peut plus considérer alors la particule comme ponctuelle.
3. Vecteur champ électrique
En exploitant la formule de la force en interaction de deux particules, on peut faire apparaître un vecteur \(\overrightarrow{E}\) (ou encore \(\overrightarrow{E'}\) selon la particule) appelé champ électrique à partir de \(\overrightarrow{F}=q'~\overrightarrow{E}\), resp. \(\overrightarrow{F'}=q~\overrightarrow{E'}\).
Pour le champ exercé par la particule de charge \(q\) sur celle de charge \(q’\) : \[\overrightarrow{E}=\frac{q}{4\pi~\varepsilon_0}~\frac{\overrightarrow{r}}{r^2}\qquad[2]\]
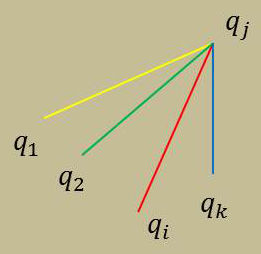 Examinons maintenant ce qui se passe lorsque plusieurs charges exercent leur action sur une charge donnée. La force exercée est la somme des forces exercées par chacune des particules prises séparément : \[\overrightarrow{F_j}=\frac{q_j}{4\pi~\varepsilon_0}~\sum_{i=1}^{i=k}q_i~\frac{r_{ij}}{r^2_{ij}}\qquad[3]\]
Examinons maintenant ce qui se passe lorsque plusieurs charges exercent leur action sur une charge donnée. La force exercée est la somme des forces exercées par chacune des particules prises séparément : \[\overrightarrow{F_j}=\frac{q_j}{4\pi~\varepsilon_0}~\sum_{i=1}^{i=k}q_i~\frac{r_{ij}}{r^2_{ij}}\qquad[3]\]
On peut écrire, naturellement (force et champ résultants) : \[\overrightarrow{E_j}=\sum_{i=1}^{i=k}\overrightarrow{E_{ij}}\quad;\quad \overrightarrow{F_j}=q_j~\overrightarrow{E_j}\qquad[4]\]
4. Distributions continues de charges
Un très grand nombre de charges contenues dans un très petit volume peut être assimilé à un élément de volume \(d\tau\). On peut considérer alors qu’il s’agit d’une distribution continue d’électricité de densité volumique \(\rho(u,~v,~w)\). Cet élément de volume porte donc une charge \(dq=\rho~d\tau\).
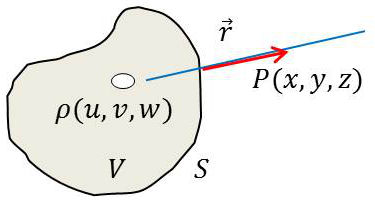 Le champ produit en un point quelconque \(P(x,~y,~z)\) par tout le volume est égal à la somme des champs produits par les différents éléments de volume. D’où l’expression de cette somme finie (intégrale étendue à tout le volume) : \[\begin{aligned} \overrightarrow{E}(x,~y,~z)&=\frac{1}{4\pi~\varepsilon_0}~\int_V\rho~\frac{\overrightarrow{r}}{r^3}~d\tau\\ \overrightarrow{E}(x,~y,~z)&=-\frac{1}{4\pi~\varepsilon_0}~\int_V\rho~\overrightarrow{\rm grad}\Big(\frac{1}{r}\Big)~d\tau \end{aligned} \qquad[5]\]
Le champ produit en un point quelconque \(P(x,~y,~z)\) par tout le volume est égal à la somme des champs produits par les différents éléments de volume. D’où l’expression de cette somme finie (intégrale étendue à tout le volume) : \[\begin{aligned} \overrightarrow{E}(x,~y,~z)&=\frac{1}{4\pi~\varepsilon_0}~\int_V\rho~\frac{\overrightarrow{r}}{r^3}~d\tau\\ \overrightarrow{E}(x,~y,~z)&=-\frac{1}{4\pi~\varepsilon_0}~\int_V\rho~\overrightarrow{\rm grad}\Big(\frac{1}{r}\Big)~d\tau \end{aligned} \qquad[5]\]
En coordonnées cartésiennes : \[d\tau=du~dv~dw\quad;\quad r=\sqrt{(x-u)^2+(y-v)^2+(z-w)^2}\]
Dans le cas de charges réparties sur une surface \(S\) (densité superficielle \(\sigma(u,~v,~w)\) : \[\overrightarrow{E}(x,~y,~z)=\frac{1}{4\pi~\varepsilon_0}~\int_S\sigma~\frac{\overrightarrow{r}}{r^3}~ds\qquad[6]\]
Dans le cas d’une distribution linéaire (densité \(\lambda(u,~v,~w)\) : \[\overrightarrow{E}(x,~y,~z)=\frac{1}{4\pi~\varepsilon_0}~\int_C\lambda~\frac{\overrightarrow{r}}{r^3}~dl\qquad[7]\]
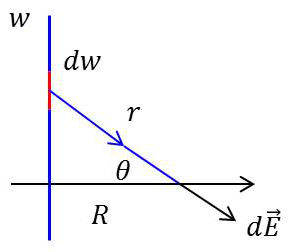 Prenons par exemple le cas d’un fil chargé de longueur infinie. L’élément de charge est : \[dq=\lambda~dw=\lambda~r~d\theta\]
Prenons par exemple le cas d’un fil chargé de longueur infinie. L’élément de charge est : \[dq=\lambda~dw=\lambda~r~d\theta\]
\(R\) : distance du point de mesure au fil chargé.
Prenons comme variable d’intégration \(\theta\) tel que \(\theta\in[-\pi/2~,~+\pi/2]\).
Notant que \(R=r~\cos\theta\). On obtient, toutes simplifications faites : \[|\overrightarrow{E}|=\frac{\lambda}{4\pi~\varepsilon_0}~\int_{-\pi/2}^{+\pi/2}\frac{\cos\theta}{R}~d\theta =\frac{\lambda}{2\pi~\varepsilon_0}~\int_0^{+\pi/2}\frac{\cos\theta}{R}~d\theta =\frac{\lambda}{2\pi~\varepsilon_0}~\frac{1}{R}\qquad[8]\]
5. Équations fondamentales du champ
Nous désignons par \(\rho\) la densité volumique de charge.
Partons de l’expression[5] de \(\overrightarrow{E}\) :
\[\overrightarrow{E}(x,~y,~z)=-\frac{1}{4\pi~\varepsilon_0}~\int_V\rho~\overrightarrow{\rm grad}\Big(\frac{1}{r}\Big)~d\tau\]
Mettant à profit les propriétés de l’analyse vectorielle, en particulier : \[\left\{ \begin{aligned} \overrightarrow{\rm rot}(\overrightarrow{\rm grad})&=\overrightarrow{0}\\ \rm div(\overrightarrow{\rm grad})&=\Delta\\ \int_V f(x,~y,~z)~\Delta\Big(\frac{1}{r}\Big)~dx~dy~dz&=-4\pi~f(u,~v,~w)~du~dv~dw\\ \overrightarrow{\rm rot}(\overrightarrow{\rm rot}\overrightarrow{E})&=\overrightarrow{\rm grad}(\rm div\overrightarrow{E})-\Delta\overrightarrow{E} \end{aligned} \right. \qquad[6]\]
On peut en déduire, tous calculs faits, que : \[\begin{aligned} \overrightarrow{\rm rot}\overrightarrow{E}&=\overrightarrow{0}\\ \rm div(\overrightarrow{E})&=-\frac{1}{4\pi~\varepsilon_0}~\int_V\rho~\Delta\Big(\frac{1}{r}\Big)~d\tau\\ \overrightarrow{D}&=\varepsilon_0~\overrightarrow{E}\quad \Rightarrow\quad \rm div(\overrightarrow{D})=\varepsilon_0~div(\overrightarrow{E})=\rho\\ \Delta\overrightarrow{E}&=\frac{\rho}{\varepsilon_0}\qquad\text{(équation de Poisson)} \end{aligned} \qquad[7]\]
Remarque
Dans tout ce qui précède, les variables \(u,~v,~w)\) ont été associées à \(\rho\) et les variables \(x,~y,~z\) ont été associées à \(\overrightarrow{r}\).
6. Théorème de Gauss
Le théorème de Gauss est issu de l’une des formes intégrales des équations du champ.
6.1. Forme 1
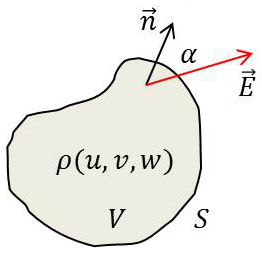 En intégrant la relation \(\overrightarrow{\rm rot}\overrightarrow{E}=\overrightarrow{0}\) dans tout le volume \(V\) limité par la surface fermée \(S\), et en transformant en intégrale de surface : \[\iint_S(\overrightarrow{n}\wedge\overrightarrow{E}~dS)=0\qquad[8]\]
En intégrant la relation \(\overrightarrow{\rm rot}\overrightarrow{E}=\overrightarrow{0}\) dans tout le volume \(V\) limité par la surface fermée \(S\), et en transformant en intégrale de surface : \[\iint_S(\overrightarrow{n}\wedge\overrightarrow{E}~dS)=0\qquad[8]\]
Formule très utile pour démontrer la continuité des composantes tangentielles du champ \(\overrightarrow{E}\) à la traversée d’une couche simple.
6.2. Forme 2
Procédons à présent à une deuxième intégration (divergence) : \[\iiint_V \rm div(\overrightarrow{D})~dv=\iiint_V~\rho~dv\]
La première intégrale se transforme en intégrale de surface et la deuxième représente la charge totale \(Q\) contenue dans le volume \(V\) : \[\iint_S(\overrightarrow{n}\cdot\overrightarrow{D})~ds=0\qquad[9]\]
Telle est la forme intégrale du théorème de Gauss :
Si l’on considère un ensemble de charges (continues, discontinues, ponctuelles, etc.) contenues dans un volume limité par une surface \(S\) fermée, le flux total à travers cette surface \(S\) est égale à la charge totale contenue dans le volume.
S’il n’y a pas de charges à l’intérieur de \(S\), on a naturellement \(Q = 0\).
7. Potentiel et circulation de champ
On peut écrire, à priori : \[\overrightarrow{\rm rot}\overrightarrow{E}=\overrightarrow{0}\qquad\Rightarrow\qquad\overrightarrow{E}=-\overrightarrow{\rm grad}(V)\qquad[10]\]
Le scalaire \(V\) est le potentiel du champ \(\overrightarrow{E}\).
S’il est défini par la formule précédente, à partir du champ, on voit qu’il est défini à une constante près, car le gradient d’une constante est toujours nul. Quand la distribution de charges qui crée le champ occupe un volume limité, on peut convenir de faire \(V = 0\) à l’infini et le potentiel est ainsi complètement défini.
L’avantage du potentiel est d’être défini par une seule fonction des coordonnées \(V(x,~y,~z)\), tandis que le champ \(\overrightarrow{E}\) est un vecteur défini par ses trois composantes, c’est-à-dire par trois fonctions de coordonnées.
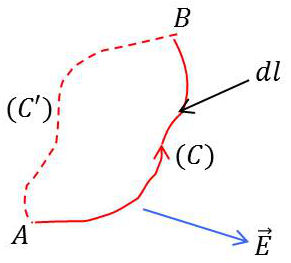 En considérant la trajectoire \(C\) ci-contre et à partir de la relation précédente, on peut écrire : \[\int_A^B\overrightarrow{E}\cdot\overrightarrow{dl}=-\int_A^B\overrightarrow{\rm grad}(V)\cdot\overrightarrow{dl}=\int_A^B d_\alpha V~dl^{\alpha}\]
En considérant la trajectoire \(C\) ci-contre et à partir de la relation précédente, on peut écrire : \[\int_A^B\overrightarrow{E}\cdot\overrightarrow{dl}=-\int_A^B\overrightarrow{\rm grad}(V)\cdot\overrightarrow{dl}=\int_A^B d_\alpha V~dl^{\alpha}\]
C’est-à-dire : \[\int_A^B\overrightarrow{E}\cdot\overrightarrow{dl}=-\int_A^B(\partial_1V~dx_1+\partial_2V~dx_2+\partial_3V~dx_3)\]
On a donc : \[\int_A^B\overrightarrow{E}\cdot\overrightarrow{dl}=-\int_A^B dV=V_A-V_B\qquad[11]\]
La circulation du champ le long de la courbe \(C\) ne dépend pas du chemin parcouru. Le résultat aurait été le même avec le trajet \(C'\). Seuls interviennent l’état initial et l’état final.
On remarque que si l’on peut faire \(V = 0\) à l’infini, l’expression du potentiel au point \(A\) est donné par l’intégrale : \[V_A=\int_A^{\infty}\overrightarrow{E}\cdot\overrightarrow{dl}\qquad[12]\]
8. Surfaces équipotentielles. Lignes de forces du champ
Le lieu des points où le potentiel garde une valeur constante est défini par \(V(x,~y,~z)=cte\). C’est une surface. De son équation on tire : \[0=dV=\frac{\partial V}{\partial x}~dx+\frac{\partial V}{\partial y}~dy+\frac{\partial V}{\partial z}~dz\]
C’est-à-dire : \[0=\overrightarrow{dl}\cdot\overrightarrow{\rm grad}(V)=-(\overrightarrow{dl}\cdot\overrightarrow{E})\]
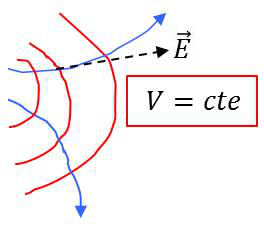 Le produit scalaire étant nul, ces deux vecteurs sont perpendiculaires. Par conséquent le vecteur \(\overrightarrow{E}\) est normal à la surface équipotentielle passant au point considéré.
Le produit scalaire étant nul, ces deux vecteurs sont perpendiculaires. Par conséquent le vecteur \(\overrightarrow{E}\) est normal à la surface équipotentielle passant au point considéré.
Comme le champ a une direction bien déterminée, il en résulte que deux parties d’une même surface équipotentielle ne peuvent se couper sous un angle fini.
En réalité, cela peut se produire, mais c’est parce qu’en ces points le champ est nul et qu’il n’y a aucune équivoque.
Par conséquent, les lignes orthogonales aux surfaces équipotentielles forment une famille de courbes qui sont tangentes au champ \(\overrightarrow{E}\) en chacun de leur point. Ce sont les lignes de force du champ électrique.
Soit \(\overrightarrow{d\lambda}(du,~dv,~dw)\) le vecteur élémentaire à une ligne de force au point \((u,~v,~w)\).
On a : \[\overrightarrow{E}=k~\overrightarrow{d\lambda}\]
d’où l’équation des lignes de force : \[\frac{du}{E_x(u,~v,~w)}=\frac{dv}{E_y(u,~v,~w)}=\frac{dw}{E_z(u,~v,~w)}\qquad[13]\]
 Les lignes de force qui s’appuient sur un contour fermé forment un tube de force.
Les lignes de force qui s’appuient sur un contour fermé forment un tube de force.
Considérons un volume limité par un tube de force et deux portions \(S'\) et \(S''\) de surfaces équipotentielles. Si ce volume se trouve dans le vide où \(\rho=0\), en y appliquant le théorème de Gauss on obtient : \[\int_S(\overrightarrow{n'}\cdot\overrightarrow{D'}~ds)+\int_S(\overrightarrow{n''}\cdot\overrightarrow{D''}~ds)+\int_S(\overrightarrow{n'''}\cdot\overrightarrow{D'''}~ds)=0\]
La dernière des trois intégrales est nulle puisque : \[\overrightarrow{n'''}\cdot\overrightarrow{D'''}=0\]
On remarque que les vecteurs unitaires sont tels que : \[\overrightarrow{n}=\overrightarrow{n'}=-\overrightarrow{n''}\]
On aura donc :
\[\begin{aligned} \overrightarrow{n}\cdot\overrightarrow{D'}=D'\quad&;\quad\overrightarrow{n}\cdot\overrightarrow{D''}=-D''\\ \int_{S'}D'~ds&=\int_{S''}D''~ds\end{aligned}\]
Si l’on considère un tube élémentaire s’appuyant sur les éléments de surface \(dS'\) et \(dS''\), on pourra écrire plus simplement :
\[\begin{aligned} D'~ds'&=D''~ds''=cte\\ E'~ds'&=E''~ds''=cte\end{aligned}\]
Ce qui exprime la conservation du flux du vecteur induction en dehors des charges.
En examinant la topologie du réseau de lignes de force et d’équipotentielles, là où se resserrent les lignes de force, le champ est plus intense et inversement.
Si les lignes de force sont des droites parallèles, c’est que le champ est uniforme.
Les lignes de force partent toujours des régions chargées positivement pour se diriger vers les régions chargées négativement ou se perdre à l’infini.

