1. Propriétés générales des diélectriques
Les milieux matériels sont des assemblages de molécules et d’atomes. Sous l’action d’un champ électrique, les charges sont déplacées :
-
les charges positives dans le sens du champ ;
-
les charges négatives en sens inverse.
Si leurs centres de gravité étaient en coïncidence initialement, le champ va les séparer.
À des distances très grandes par rapport aux distances des charges entre elles dans l’atome, la molécule se comporte comme un petit dipôle.
Dans un atome les électrons sont déplacés par rapport aux noyaux : c’est la polarisation électronique. Dans un cristal ionique, il y aura un déplacement d’ions (\(+,-\)) en sens contraire : c’est la polarisation ionique.
Les molécules étant nombreuses dans un petit volume, même pour un gaz dans les conditions habituelles, on peut faire l’hypothèse d’une distribution continue de dipôles. On définit ainsi un moment dipolaire \(\overrightarrow{P}\) par unité de volume. Un petit élément de volume aura donc un moment dipolaire \(\overrightarrow{P}~dv\).
Une telle répartition volumique de dipôles produit par elle-même un champ électrique qui tend à s’opposer à la cause qui lui a donné naissance (loi générale). C’est un champ dépolarisant qui, dans la matière, diminue le champ initial.
Nous avons supposé que les centres de gravité des charges \([+]\) et \([-]\) coïncidaient en l’absence de champ. Cela n’est pas toujours le cas et les molécules possèdent souvent un moment dipolaire permanent. C’est le cas des molécules \(HCl,~H_2O,~SO_2\), etc.
En l’absence de champ extérieur, ces moments dipolaires sont disposés en désordre et on peut admettre, en moyenne, qu’un petit élément de volume a un moment nul.
Quand ces molécules sont placées dans un champ extérieur, il apparaît deux effets :
-
un effet de déformation ;
-
un effet d’orientation sur les dipôles permanents préexistants.
Ce dernier contribue aussi à transformer un élément de volume en un dipôle. Il est en général prépondérant, du moins pour les champs constants que nous considérons ici.
Cet effet d’orientation est contrarié par l’effet des chocs moléculaires ; ces derniers étant d’autant plus nombreux que la température est plus élevée, le moment \(\overrightarrow{P}\) qui apparaît ainsi par unité de volume dépend de la température.
Au contraire, les déformations sont indépendantes des chocs donc de la température.
Dans les diélectriques parfaits tous les électrons gravitent autour des noyaux d’atomes et il n’y a pas d’électrons libres comme dans les métaux. En fait, le diélectrique parfait n’existe pas vraiment et le diélectriques réel est peu conducteur.
2. Équations du champ
Rappelons les relations : \[[1]\qquad \left\{ \begin{aligned} \overrightarrow{\rm rot}(\overrightarrow{E})&=\overrightarrow{0}\\ \rm div(\overrightarrow{D})&=\rho\\ \overrightarrow{D}&=\varepsilon_0~\overrightarrow{E}+\overrightarrow{P} \end{aligned} \right.\]
Dans le cas du diélectrique isotrope, nous poserons : \[\overrightarrow{P}=\chi~\overrightarrow{E}=\varepsilon_0~\chi_r~\overrightarrow{E}\qquad[2]\]
-
\(\chi,~\chi_r\) : susceptibilités absolue et relative du milieu considéré
-
\(\chi_r\) : constante caractéristique de la substance dans des conditions déterminées (température, pression, etc.)
Pour un diélectrique parfait et dans les conditions habituelles de température et de pression, la susceptibilité ne dépend pratiquement pas du champ \(\overrightarrow{E}\). On a toujours \(\chi_r>0\). Ceci, contrairement aux susceptibilités magnétiques (positives ou négatives).
On a donc : \[\overrightarrow{D}=\varepsilon_0~(1+\chi_r)~\overrightarrow{E}\qquad[3]\]
Posons : \[\varepsilon=\varepsilon_0~(1+\chi_r)=\varepsilon_0~\varepsilon_r=\varepsilon_0+\chi\qquad[4]\]
Les équations fondamentales peuvent alors s’écrire : \[\begin{aligned} \overrightarrow{P}&=(\varepsilon-\varepsilon_0)~\overrightarrow{E}=\Big(1-\frac{\varepsilon_0}{\varepsilon}\Big)~\overrightarrow{D}\\ \overrightarrow{D}&=\varepsilon~\overrightarrow{E} \end{aligned} \qquad[5]\]
-
\(\varepsilon\) : perméabilité électrique absolue de la substance
-
\(\varepsilon_r\) : perméabilité relative au vide
Elles sont appelées aussi constante diélectrique ou pouvoir inducteur spécifique. \[\varepsilon_r=1+\chi_r=\frac{\varepsilon}{\varepsilon_0}\qquad[6]\]
\(\chi,~\varepsilon\) peuvent être fonctions des {\(x,~y,~z\)}, de la température, de la pression, etc.
3. Potentiel
Des deux relations : \[\left\{ \begin{aligned} \overrightarrow{D}&=\varepsilon~\overrightarrow{E}\\ \rm div(\overrightarrow{D})&=\rho \end{aligned} \right.\]
il vient : \[\varepsilon~\rm div(\overrightarrow{E})=-\big\{\overrightarrow{E}\cdot\overrightarrow{\rm grad}(\varepsilon)\big\}+\rho\]
Sachant que : \[\overrightarrow{E}=-\overrightarrow{\rm grad}(V)\]
il vient \[\Delta V=-\frac{1}{\varepsilon}~\big\{\overrightarrow{\rm grad}(V)\cdot\overrightarrow{\rm grad}(\varepsilon)+\rho\big\}\qquad[7]\]
Si le milieu est homogène : \[\overrightarrow{\rm grad}(\varepsilon)=0\quad\Rightarrow\quad\Delta V=-\frac{\rho}{\varepsilon}\qquad[8]\]
expression identique à l’équation de Poisson dans le vide, \(\varepsilon\) a remplacé \(\varepsilon_0\).
Si \(V_0\) est une solution pour une certaine distribution de charges dans le vide : \[\varepsilon~V=\varepsilon_0~V_0\qquad\text{ou encore :}\quad V=\frac{V_0}{\varepsilon_r}\qquad[9]\]
Dans la plupart des cas, il n’y a pas de charges vraies à l’intérieur des diélectriques ; on aura donc \(\rho=0\) et l’équation du potentiel se réduira à l’équation de Laplace. C’est ce qui fait l’intérêt du potentiel, car les solutions de cette équation sont bien connues.
4. Surface de séparation de deux diélectriques, conditions aux limites
Rappelons les conditions établies précédemment : \[\begin{aligned} \overrightarrow{n}\wedge(\overrightarrow{E_1}-\overrightarrow{E_2})&=\overrightarrow{0}\\ \overrightarrow{n}\cdot(\overrightarrow{D_1}-\overrightarrow{D_2})&=\sigma \end{aligned} \qquad[10]\]
\(\sigma\) : densité superficielle des charges vraies sur la surface \(S\) de séparation. Dans de très nombreux cas, il n’y a pas de charges vraies (\(\sigma=0\)).
Le système de relations [10] signifie que :
-
les composantes tangentielles de \(\overrightarrow{E}\) ainsi que les composantes normales de \(\overrightarrow{D}\) sont continues à la traversée de la surface ;
-
les composantes normales de \(\overrightarrow{E}\) et les composantes tangentielles de \(\overrightarrow{D}\) ne sont pas continues dans les mêmes conditions.
Il suffit pour cela de reprendre l’écriture des relations : \[\begin{aligned} \overrightarrow{n}\wedge(\frac{\overrightarrow{D_1}}{\varepsilon_1}-\frac{\overrightarrow{D_1}}{\varepsilon_1})&=0\\ \overrightarrow{n}\cdot(\varepsilon_1~\overrightarrow{E_1}-\varepsilon_2~\overrightarrow{E_2})&=\sigma \end{aligned} \qquad[11]\]
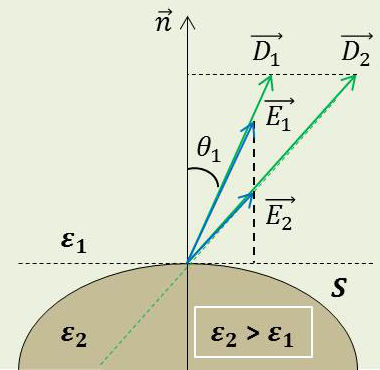 On peut écrire lorsque \(\sigma=0\) : \[\begin{aligned} E_{1t}&=E_{2t}\\ \varepsilon_1~E_{1n}&=\varepsilon_2~E_{2n} \end{aligned} \qquad[12]\]
On peut écrire lorsque \(\sigma=0\) : \[\begin{aligned} E_{1t}&=E_{2t}\\ \varepsilon_1~E_{1n}&=\varepsilon_2~E_{2n} \end{aligned} \qquad[12]\]
Ou bien encore : \[\begin{aligned} E_1~\sin\theta_1&=E_2~\sin\theta_2\\ \varepsilon_1~E_1~\cos\theta_1&=\varepsilon_2~E_2~\cos\theta_2 \end{aligned} \qquad[13]\]
On en déduit : \[\varepsilon_1~\cot\theta_1=\varepsilon_2~\cot\theta_2\qquad[14]\]
équation régissant la réfraction des lignes de force du champ électrique, lignes qui coïncident d’ailleurs avec les lignes d’induction puisque (\(\overrightarrow{D}\) et \(\overrightarrow{E}\) colinéaires dans les milieux isotropes).
Les conditions aux limites pour le potentiel correspondent aux conditions des champs : \[\begin{aligned} \overrightarrow{n}\wedge(\overrightarrow{E_1}-\overrightarrow{E_2})&=\overrightarrow{0}\\ \overrightarrow{n}\cdot(\overrightarrow{D_1}-\overrightarrow{D_2})&=\sigma \end{aligned} \qquad[15]\]
Elles s’écrivent : \[\begin{aligned} (V_1)_S&=(V_2)_S\\ \Big(\varepsilon_1~\frac{\partial V_1}{\partial n}-\varepsilon_2~\frac{\partial V_2}{\partial n}\Big)_S&=\sigma \end{aligned} \qquad[16]\]
Conditions très pratiques quand \(\sigma=0\).
5. Conducteur plongé dans un diélectrique
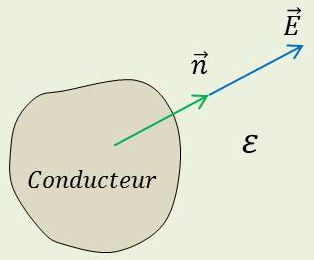 Le champ étant nul à l’intérieur du conducteur, la première condition s’écrit : \[\overrightarrow{n}\wedge\overrightarrow{E}=\overrightarrow{0}\qquad[17]\]
Le champ étant nul à l’intérieur du conducteur, la première condition s’écrit : \[\overrightarrow{n}\wedge\overrightarrow{E}=\overrightarrow{0}\qquad[17]\]
La composante tangentielle du champ au voisinage immédiat de la surface, et à l’extérieur, est nulle.
La valeur de la composante normale est donnée par : \[\overrightarrow{n}\cdot(\overrightarrow{D}-\overrightarrow{0})=\varepsilon~(\overrightarrow{n}\cdot\overrightarrow{E})=\sigma\quad\Rightarrow\quad E_n=\frac{\sigma}{\varepsilon}\qquad[18]\]
Pour une même densité superficielle de charge au voisinage immédiat d’un conducteur, le champ est \(\varepsilon_r\) fois plus petit dans un diélectrique que dans le vide.
Un conducteur peut être considéré comme un diélectrique de constante diélectrique infinie.
6. Lame à faces parallèles dans un champ uniforme
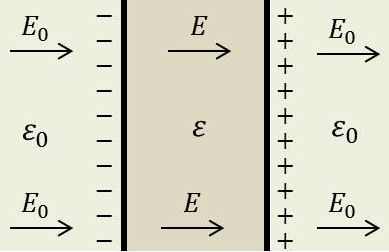 Une lame à faces parallèles est supposée indéfinie, de constante diélectrique \(\varepsilon\). Le champ influençant est supposé uniforme, fixe et normal à la lame ; il est désigné par \(\overrightarrow{E_0}\).
Une lame à faces parallèles est supposée indéfinie, de constante diélectrique \(\varepsilon\). Le champ influençant est supposé uniforme, fixe et normal à la lame ; il est désigné par \(\overrightarrow{E_0}\).
On peut adopter comme solution un champ constant \(\overrightarrow{E}\) à l’intérieur, de même direction et de même sens que le champ initial \(\overrightarrow{E_0}\).
Dans ces conditions le champ produit par la polarisation est nul à l’extérieur où le champ est donc égal au champ initial \(\overrightarrow{E_0}\).
Pour connaître \(\overrightarrow{E}\) intérieur, on écrit que les conditions aux limites sont satisfaites : \[\varepsilon~\overrightarrow{E}=\varepsilon_0~\overrightarrow{E_0}\qquad[19]\]
Comme \(\varepsilon>\varepsilon_0\), le champ intérieur est toujours plus petit que le champ initial. Ceci est dû au fait que les dipôles induits dans le diélectrique créent un champ qui s’oppose au champ inducteur.
Il est facile de trouver ici les charges fictives de polarisation. Partant de relations précédentes, (avec \(\varepsilon=cte\)) : \[\sigma'=\overrightarrow{n}\cdot\overrightarrow{P}\quad;\quad \rho'=-\rm div(\overrightarrow{P})\qquad[20]\]
Il vient : \[\begin{aligned} \rho'&=-\rm div(\overrightarrow{P})=-(\varepsilon-\varepsilon_0)~div(\overrightarrow{E})=0\\ \sigma'&=\overrightarrow{n}\cdot\overrightarrow{P}=(\varepsilon-\varepsilon_0)~(\overrightarrow{n}\cdot\overrightarrow{E}) \end{aligned} \qquad[21]\]
Mais on a ici, suivant la face : \[\overrightarrow{n}\cdot\overrightarrow{E}=\pm~E\quad(\text{droite/gauche})\]
Le champ dû aux quadripôles est le même que celui créé par deux couches de densité : \[\sigma'=\pm(\varepsilon-\varepsilon_0)~\overrightarrow{E}\qquad[22]\]
Nous avons vu qu’une telle distribution de charge créait :
-
à l’extérieur un champ nul ;
-
à l’intérieur un champ : \[\overrightarrow{\mathcal{E}}=-\frac{|\sigma'|}{\varepsilon_0}=-\frac{|\varepsilon-\varepsilon_0|}{\varepsilon_0}~\overrightarrow{E}=-\frac{|\varepsilon-\varepsilon_0|}{\varepsilon}~\overrightarrow{E_0}\qquad[23]\]
Ce dernier, on le sait, est opposé au champ \(\overrightarrow{E}\). C’est pour cela qu’on l’appelle parfois le champ dépolarisant.
Le champ réel est la somme du champ initial et du champ dû à la polarisation : \[\overrightarrow{E}=\overrightarrow{E_0}+\overrightarrow{\mathcal{E}}\qquad[24]\]
7. Condensateur plan avec lames diélectriques
7.1. Premier cas
Soient \(\overrightarrow{E_1},~\overrightarrow{E_2},~\overrightarrow{E_3}\) les champs dans trois diélectriques de perméabilité \(\varepsilon_1,~\varepsilon_2,~\varepsilon_3\).
\(V=V_A-V_B\) étant la différence de potentiel entre les deux plateaux.
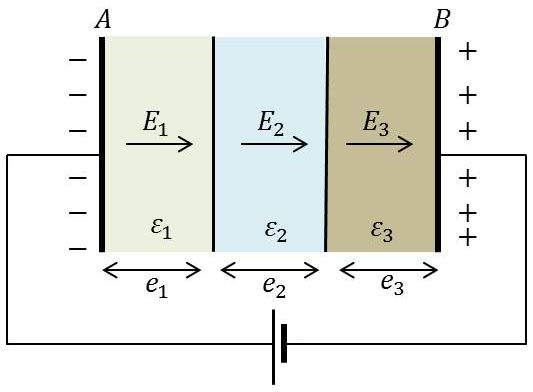 Les lames sont parallèles aux plateaux et si l’on néglige les perturbations dues aux bords les surfaces équipotentielles sont aussi des plans parallèles aux plateaux.
Les lames sont parallèles aux plateaux et si l’on néglige les perturbations dues aux bords les surfaces équipotentielles sont aussi des plans parallèles aux plateaux.
Les champs sont tous dirigés suivant les normales aux surfaces de séparation.
Les conditions aux limites sur ces surfaces s’écrivent : \[\begin{aligned} D_1&=D_2=D_3\\ \varepsilon_1~E_1&=\varepsilon_2~E_2=\varepsilon_3~E_3 \end{aligned} \qquad[25]\]
On peut donc exprimer tous les champs en fonction de l’un d’eux, \(E_1\) par exemple : \[E_2=\frac{\varepsilon_1}{\varepsilon_2}~E_1\quad;\quad E_3=\frac{\varepsilon_1}{\varepsilon_3}~E_1\]
Nous obtenons une première relation en écrivant que la circulation du champ électrique entre les deux plateaux est égale à la différence de potentiel, soit : \[V=V_A-V_B=e_1~E_1+e_2~E_2+e_3~E_3=\Big(e_1+\frac{\varepsilon_1}{\varepsilon_2}~e_2+\frac{\varepsilon_1}{\varepsilon_3}~e_3\Big)~E_1\qquad[26]\]
Une troisième relation est donnée par les conditions aux limites sur les plateaux : \[D_1=\sigma\quad\text{ou}\quad\varepsilon_1~E_1=\sigma\qquad[27]\]
\(\sigma\) : densité de charge sur les plateaux
\(Q=\sigma~S\) étant la charge totale sur la plaque positive de surface \(S\) : \[V=\Big(\frac{e_1}{\varepsilon_1}+\frac{e_2}{\varepsilon_2}+\frac{e_3}{\varepsilon_3}\Big)~\sigma=\Big(\frac{e_1}{\varepsilon_1}+\frac{e_2}{\varepsilon_2}+\frac{e_3}{\varepsilon_3}\Big)~\frac{Q}{S}\qquad[28]\]
D’où l’expression de la capacité : \[V=\frac{S}{\cfrac{e_1}{\varepsilon_1}+\cfrac{e_2}{\varepsilon_2}+\cfrac{e_3}{\varepsilon_3}}\qquad[29]\]
On aurait pu obtenir cette formule en supposant une mise en série de trois condensateurs.
Si l’on a un diélectrique unique entre les deux plateaux, on pose : \[\begin{aligned} &e_1+e_2+e_3=e\\ &\varepsilon_1=\varepsilon_2=\varepsilon_3=\varepsilon \end{aligned} \qquad[30]\]
Il vient ce résultat connu depuis longtemps : \[C=\frac{\varepsilon~S}{e}=\frac{Q}{V}=\frac{\sigma~S}{V}\qquad[31]\]
Comparons la densité de charge \(\sigma\) dans ce dernier cas à la densité \(\sigma_0\) quand il y a le vide entre les deux plateaux. Pour une même différence de potentiel, on obtient : \[\frac{\sigma}{\sigma_0}=\frac{\varepsilon}{\varepsilon_0}\qquad[32]\]
Ainsi, la densité est multipliée par \(\varepsilon/\varepsilon_0\) quand on introduit le diélectrique. C’est le générateur qui fournit les charges supplémentaires. Les capacités sont dans le même rapport : \[\frac{C}{C_0}=\frac{\varepsilon}{\varepsilon_0}\qquad[33]\]
On traiterait d’une manière analogue le cas d’un nombre quelconque de lames entre les deux plateaux. Ce qui donnerait une capacité : \[C=\frac{S}{\sum_i\cfrac{e_i}{\varepsilon_i}}\qquad[34]\]
7.2. Deuxième cas
Maintenant, le condensateur contient deux diélectriques. En négligeant toujours les effets de bords, les équipotentielles sont des plans parallèles aux plateaux et leur champ est partout normal.
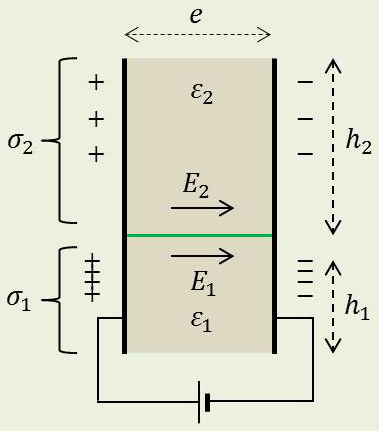 D’après la condition aux limites entre les deux diélectriques : \[E_1=E_2\qquad[35]\]
D’après la condition aux limites entre les deux diélectriques : \[E_1=E_2\qquad[35]\]
Pour la condition aux limites sur les plateaux : \[\sigma_1=\varepsilon_1~E_1\quad;\quad\sigma_2=\varepsilon_2~E_2\quad\Rightarrow\quad\frac{\sigma_1}{\sigma_2}=\frac{\varepsilon_1}{\varepsilon_2}\qquad[36]\]
Les densités de charge ne sont donc pas les mêmes sur les différentes parties du plateau.
Pour la charge totale \(Q\) du plateau positif, on peut écrire, (\(l\) étant la largeur du condensateur) : \[\begin{aligned} &Q=\sigma_1~s_1+\sigma_2~s_2=l~(\sigma_1~h_1+\sigma_2~h_2)\\ &Q=\frac{l}{e}~(\sigma_1~h_1+\sigma_2~h_2)~V \end{aligned} \qquad[37]\]
D’où pour la capacité : \[\begin{aligned} &C=\frac{l}{e}~(\sigma_1~h_1+\sigma_2~h_2)=\frac{\sigma_1~h_1+\sigma_2~h_2}{h_1+h_2}\frac{S}{e}\\ &C=\frac{\varepsilon_1~S_1}{e}+\frac{\varepsilon_2~S_2}{e}=C_1+C_2 \end{aligned} \qquad[37]\]
On aurait pu obtenir ce résultat par la formule de l’association des condensateurs en série.
8. Condensateur cylindrique avec diélectrique
Dans le cas d’un condensateur cylindrique, on peut satisfaire aux conditions aux limites avec des expressions de la forme : \[E_r=\frac{k}{r}\qquad[38]\]
Mais la constante \(k\) prend des valeurs différentes dans différentes régions.
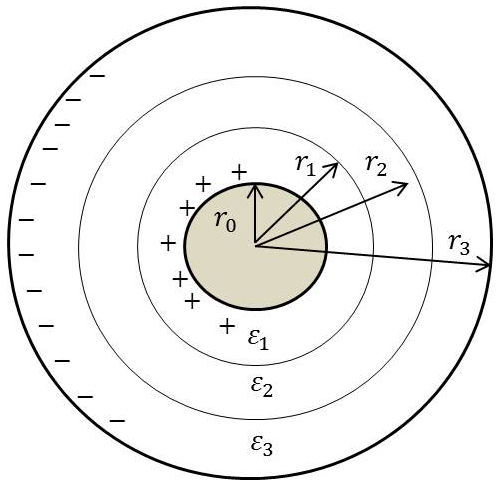 Condition aux limites sur l’armature interne : \[(E_1)_{r=r_0}=\frac{k}{r_0}=\frac{\sigma_0}{\varepsilon_1}\qquad[39]\]
Condition aux limites sur l’armature interne : \[(E_1)_{r=r_0}=\frac{k}{r_0}=\frac{\sigma_0}{\varepsilon_1}\qquad[39]\]
Il vient : \[k=\frac{r_0.\sigma_0}{\varepsilon_1}\quad;\quad E_1=\frac{r_0~\sigma_0}{\varepsilon_1~r}\qquad[40]\]
\(\sigma_0\) : densité superficielle de charge sur \(r=r_0\)
La condition aux limites (\(r=r_1\) ) donne : \[\begin{aligned} (E_2)_{r=r_1}&=\frac{\varepsilon_1}{\varepsilon_2}~(E_1)_{r=r_1}=\frac{r_0~\sigma_0}{\varepsilon_2~r_1}\\ E_2&=\frac{r_0~\sigma_0}{\varepsilon_2~r} \end{aligned} \qquad[41]\]
La même condition aux limites (\(r=r_2\) ) donne : \[\begin{aligned} (E_3)_{r=r_1}&=\frac{\varepsilon_2}{\varepsilon_3}(E_2)_{r=r_2}=\frac{r_0~\sigma_0}{\varepsilon_3~r_2}\\ E_3&=\frac{r_0~\sigma_0}{\varepsilon_3~r} \end{aligned} \qquad[42]\]
Écrivons que la circulation du champ entre les deux armatures, calculée le long du rayon est égale à la différence de potentiel (\(V=V_0-V_3\)) : \[\begin{aligned} &V=r_0~\sigma_0~\Big\{\frac{1}{\varepsilon_1}\int_{r0}^{r1}\frac{dr}{r}+\frac{1}{\varepsilon_2}\int_{r1}^{r2}\frac{dr}{r}+\frac{1}{\varepsilon_3}\int_{r2}^{r3}\frac{dr}{r}\Big\}\\ &V=r_0~\sigma_0~\Big\{\frac{1}{\varepsilon_1}~\ln\frac{r_1}{r_0}+\frac{1}{\varepsilon_2}~\ln\frac{r_2}{r_1}+\frac{1}{\varepsilon_3}~\ln\frac{r_3}{r_2}\Big\} \end{aligned} \qquad[43]\]
\(l\) étant la longueur du condensateur, la charge totale de l’armature interne est : \[Q=2\pi~r_0~\sigma_0~l\qquad[44]\]
D’où l’expression de la capacité : \[C=\frac{2\pi~l}{\cfrac{1}{\varepsilon_1}~\ln\cfrac{r_1}{r_0}+\cfrac{1}{\varepsilon_2}~\ln\cfrac{r_2}{r_1}+\cfrac{1}{\varepsilon_3}~\ln\cfrac{r_3}{r_2}}\qquad[45]\]
Formule que l’on aurait obtenue directement par la loi d’association en série.
De même pour un condensateur sphérique à couches diélectrique différentes : \[C=\frac{4\pi}{\cfrac{1}{\varepsilon_1}~\Big(\cfrac{1}{r_0}-\cfrac{1}{r_1}\Big)+\cfrac{1}{\varepsilon_2}~\Big(\cfrac{1}{r_1}-\cfrac{1}{r_2}\Big)+\cfrac{1}{\varepsilon_3}~\Big(\cfrac{1}{r_2}-\cfrac{1}{r_3}\Big)}\qquad[46]\]
9. Influence d’une charge ponctuelle sur un dioptre plan
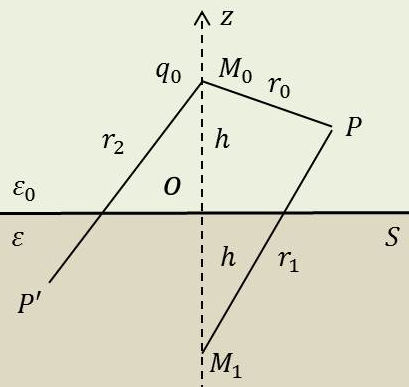 Une charge est placée en \(M_0\).
Une charge est placée en \(M_0\).
\(S\) est la surface plane de séparation entre le vide et le diélectrique de constante \(\varepsilon_0\).
Calculons le potentiel en un point \(P\) situé du même côté que la charge d’influence \(q_0\) par rapport à \(S\) : \[V=\frac{1}{4\pi~\varepsilon_0}~\Big(\frac{q_0}{r_0}-\frac{q_1}{r_1}\Big)\quad;\quad OM=OM_0\qquad[47]\]
Le potentiel \(V'\) en un point \(P'\) situé au-dessous de \(S\) est de la forme : \[V'=\frac{1}{4\pi~\varepsilon}~\frac{q_2}{r_2}\qquad[48]\]
En écrivant les conditions aux limites sur S : \[V_S=V'_S\quad;\quad\varepsilon_0~(E_n)_S=\varepsilon~(E'_n)_S\qquad[49]\]
On obtient : \[q_1=\frac{\varepsilon-\varepsilon_0}{\varepsilon+\varepsilon_0}~q_0\quad;\quad q_2=\frac{2\varepsilon}{\varepsilon+\varepsilon_0}~q_0\qquad[50]\]
Les grandeurs \(q_1\) et \(q_2\) sont donc bien des constantes.
Des résultats que nous venons d’obtenir concernant les champs, il résulte que la charge \(q_0\) est attirée par le diélectrique avec une force (loi de Coulomb) : \[f=\frac{1}{4\pi~\varepsilon_0}~\frac{q_0~q_1}{4~h^2}=\frac{1}{4\pi~\varepsilon_0}~\frac{\varepsilon-\varepsilon_0}{\varepsilon+\varepsilon_0}~\frac{q_0^2}{4~h^2}\qquad[51]\]
10. Influence d’un champ quelconque sur un dioptre plan
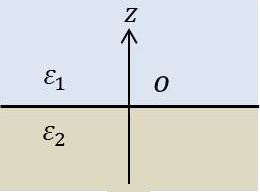 Soit \(V=f(x,~y,~z)\) le potentiel existant dans un milieu de constante diélectrique \(\varepsilon_1\), occupant tout l’espace, les sources de ce potentiel se trouvant dans la région des \(z\) positifs.
Soit \(V=f(x,~y,~z)\) le potentiel existant dans un milieu de constante diélectrique \(\varepsilon_1\), occupant tout l’espace, les sources de ce potentiel se trouvant dans la région des \(z\) positifs.
Remplaçons le diélectrique \(\varepsilon_1\) par un diélectrique \(\varepsilon_2\) dans la région des \(z\) négatifs.
Les deux diélectriques sont supposés homogènes.
Les nouveaux potentiels dans chacune des régions sont respectivement : \[\begin{aligned} V_1&=f(x,~y,~z)-A~f(x,~y,~-z)\\ V_2&=(1-A)~f(x,~y,~z)\qquad\text{A constante} \end{aligned} \qquad[52]\]
En effet, la condition suivante est remplie : \[(V_1)_{z=a}=(V_2)_{z=0}\qquad[53]\]
Par ailleurs, la condition : \[\varepsilon_1~\Big(\frac{\partial V_1}{\partial z}\Big)_{z=0}=\varepsilon_2~\Big(\frac{\partial V_2}{\partial z}\Big)_{z=0}\qquad[54]\]
entraîne : \[\varepsilon_1~(1+A)=\varepsilon_2~(1-A)\qquad[55]\]
On a donc : \[A=\frac{\varepsilon_2-\varepsilon_1}{\varepsilon_2+\varepsilon_1}\quad;\quad 1-A=\frac{2~\varepsilon_1}{\varepsilon_2+\varepsilon_1}\qquad[56]\]
En particulier, le champ donné est celui qui est produit par une source ponctuelle placée du côté des \(z\) positifs. On retrouve la formule du précédent paragraphe.

