1. Flexion d’une barre

Considérons une barre cylindrique limitée par deux sections droites. Celle qui constitue l’extrémité de gauche est maintenue en position fixe : on dit que la barre est encastrée. Appliquons à cette barre un système d’efforts quelconque : la barre prend une certaine forme d’équilibre que nous nous proposons d’étudier.

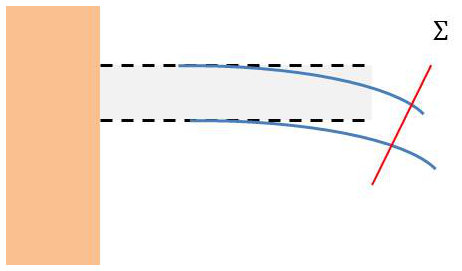Soit alors une section droite quelconque \(\Sigma\) de la barre ; la portion de barre située à droite de \(\Sigma\) est en équilibre sous l’action des forces extérieures auxquelles elle est soumise et des tensions qu’exerce sur elle la portion de gauche au travers de la surface \(\Sigma\).

Soient \(\overrightarrow{R}\) et \(\overrightarrow{C}\) la résultante générale et le moment résultant, par rapport au centre de gravité \(G\) de \(\Sigma\) de l’ensemble des forces extérieures appliquées à la portion de droite.

L’ensemble des tensions qu’exerce, au travers de \(\Sigma\), la portion de gauche sur celle de droite, peut être représenté par sa résultante générale \([-\overrightarrow{R} ]\) appliquée en \(G\) et son moment résultant \([-\overrightarrow{C}]\) par rapport à \(G\).

Lorsqu’un système de forces quelconque agit sur un solide indéformable, il est strictement équivalent à l’ensemble d’une force appliquée par exemple au centre de gravité (résultante générale) et d’un couple (moment résultant). Ici, il ne s’agit pas bien entendu d’un solide indéformable puisque ce sont précisément les déformations que nous voulons étudier et les points d’application des efforts extérieurs ont une influence notable sur les déformations de la barre en leur voisinage immédiat.

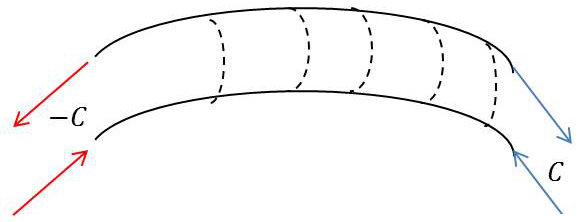La figure ci-contre montre par exemple les différences d’aspect des sections terminales, lors de l’application de deux couples opposés aux extrémités, celui de gauche étant créé par deux forces appliquées à la partie supérieure et inférieure de la section, celui de droite par un ensemble d’efforts normaux variant progressivement d’un point à l’autre.

On peut démontrer, et nous l’admettrons, que le mode de répartition des efforts extérieurs n’a d’influence notable qu’au voisinage immédiat de leur point d’application. En dehors, nous pourrons admettre que l’état de déformation de la barre, au voisinage d’une section \(\Sigma\) quelconque, ne dépend que de la résultante \(-\overrightarrow{R}\) et du moment résultant \(\overrightarrow{C}\) des efforts extérieurs exercés sur la partie de droite, vecteurs qui se trouvent équilibrés par les réactions de la partie gauche et que nous réduisons à leur résultante \(-\overrightarrow{R}\) et à leur moment résultant \(-\overrightarrow{C}\) par rapport à \(G\).

Ces déformations peuvent se classer en :

• déformation par traction dont la composante longitudinale de \(\overrightarrow{R}\) se trouve responsable ;

• déformation de flexion due aux composantes transversales de \(\overrightarrow{R}\) et de \(\overrightarrow{C}\) ;

• déformation par torsion due à la composante longitudinale de \(\overrightarrow{C}\).

Nous supposerons tout d’abord nulles les composantes longitudinales de \(\overrightarrow{R}\) et de \(\overrightarrow{C}\). Nous supposerons également que l’ensemble formé par la barre et le système des efforts qui lui sont appliqués admet le plan de figure comme plan de symétrie. Ce plan de symétrie contient les centres de gravité de toutes les sections droites, avant et après application des efforts.

Nous désignerons sous le nom de fibres les petits tubes de matière qui, avant déformation, étaient limités par des cylindres de génératrices parallèles à celles de la barre.

Supposons que la barre, après déformation tourne sa concavité vers le haut. Dans le plan de la figure, les fibres supérieures se sont raccourcies, les fibres inférieures se sont allongées. Il existe donc une fibre qui ne s’est ni allongée, ni raccourcie, et qui constitue la fibre neutre.

1.1. Flexion circulaire

Plaçons-nous d’abord dans le cas simple où la résultante \(-\overrightarrow{R}\) des efforts intérieurs qui s’exercent sur une section quelconque est nulle. Il suffit pour cela que la résultante \(\overrightarrow{R}\) des efforts extérieurs qui s’exerce sur la partie de droite de la barre soit nulle, quelle que soit la section considérée, donc que les efforts extérieurs se réduisent à des couples.

Nous étudierons le cas particulièrement simple où, les forces de pesanteur étant négligeables, on exerce sur l’extrémité de droite de la barre un couple \(-\overrightarrow{C}\) . Le support où la barre est encastrée exerce donc le couple \(-\overrightarrow{C}\) à l’autre extrémité. Nous ne chercherons pas à savoir par quelle distribution d’efforts, ce qui revient à négliger d’éventuelles perturbations aux extrémités.

En une section quelconque, les efforts appliqués par la portion de gauche équilibrent le couple \(\overrightarrow{C}\) et se réduisent à \(-\overrightarrow{C}\). Il en résulte, si nous considérons la portion de barre comprise entre deux sections quelconques, qu’elle est en équilibre sous l’action de deux couples symétriques \(-\overrightarrow{C}\) et \(\overrightarrow{C}\) appliqués à ses extrémités et que sa section médiane reste donc plane.

Toutes les sections droites de la barre restent donc planes et normales à la direction locale de la fibre neutre. Le couple appliqué étant partout le même, la forme prise par la fibre neutre est celle d’une circonférence.

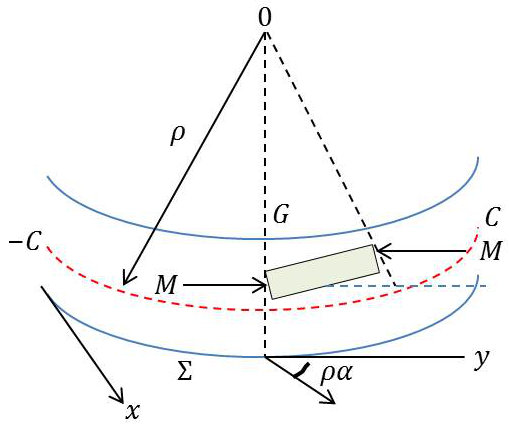
Soit \(O\) le centre de cette circonférence. Toutes les sections droites sont transformées, après déformation, en des plans passant par la perpendiculaire en \(O\) au plan de figure, et toutes les fibres du plan de symétrie ont leur centre de courbure en \(O\). Nous désignerons par \(\rho\) le rayon de courbure de la fibre neutre.

Soit alors \(y\) l’ordonnée d’une fibre quelconque, l’origine des ordonnées étant placée sur la fibre neutre, et les ordonnées étant comptées positivement vers le centre de courbure \(O\) de la fibre. L’allongement relatif de la portion \(MM'\) quelconque de cette fibre est égal à \(-y/\rho\). Elle est donc soumise à un effort de traction par unité de section : \[N=-\frac{E~y}{\rho}\]

La section \(\Sigma\) est donc soumise de la part de la portion de gauche de la barre à l’ensemble des efforts \(N~d~\sigma\) appliquée aux diverses fibres. Écrivons que leur résultante générale est nulle. \[\iint_{\Sigma} y~N~d\sigma=-\frac{E}{\rho}\iint_{\Sigma} y~d\sigma=0\]

Ce qui veut dire que la quantité sous intégrale est nulle et que, par suite, la fibre neutre située dans le plan de symétrie contient le centre de gravité de la section \(\Sigma\). Cette fibre neutre est donc constituée par l’ensemble des centres de gravité des diverses sections droites de la barre.

Écrivons que le moment résultant de l’ensemble des efforts exercés de la gauche sur \(\Sigma\) est égal à \(-\overrightarrow{C}\) : \[\iint_{\Sigma} y~N~d\sigma=-C\quad\Rightarrow\quad C=\frac{E}{\rho}\iint_{\Sigma} y^2~d\sigma=\frac{E}{\rho}~I\]

\(I\) représente le moment d’inertie de la section droite \(\Sigma\) par rapport à la perpendiculaire au plan de la figure passant par son centre de gravité.

Désignant par \(\alpha\) l’angle (petit) dont ont tourné les génératrices de la barre, au voisinage de la section \(\Sigma\), à partir de leur direction initiale, nous pourrons écrire : \[\frac{1}{\rho}=\frac{d\alpha}{dx}\quad\Rightarrow\quad C=\frac{E}{\rho}~I=\frac{d\alpha}{dx}\]

x étant l’abscisse de la section droite \(\Sigma\) à partir de l’extrémité de gauche, avant déformation, ou encore l’arc de fibre neutre entre l’extrémité de gauche et la section \(\Sigma\).

Si l’angle \(\alpha\) est partout petit, on pourra écrire : \[\alpha=\frac{dy}{dx}\qquad\text{et}\qquad C=E~I~\frac{d^2I}{dx^2}\]

1.2. Cas général de la flexion plane

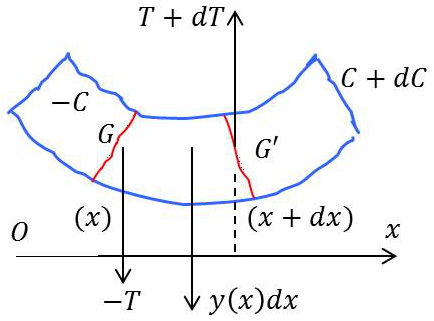À la tranche comprise entre \(x\) et \(x + dx\) est appliquée une force extérieure (gravité par exemple) \(y(x)~dx\) dirigée perpendiculairement à la direction générale \(Ox\) de la barre avant déformation. Nous nous restreignons donc à des efforts de flexion, sans traction dans le sens de l’axe de la barre.

En plus du moment fléchissant apparaît en chaque section \(\Sigma\) un effort tangentiel ou effort tranchant \(T(x)\). En fait, cet effort est dirigé normalement à la direction qu’avaient les génératrices avant déformation, mais nous supposerons petites les flexions, ce qui revient à dire que \(T\) est partout pratiquement confondu avec le plan de la section droite.

On voit sur la figure que l’élément \(dx\) de la barre est soumis aux efforts suivants :

1. Sur sa face de gauche (x) :

   \(-\overrightarrow{T}\) équilibrant la résultante générale des efforts extérieurs exercés sur la portion de barre située à droite de la section \(x\),

   \(-\overrightarrow{C}\) équilibrant le moment résultant de ces mêmes efforts par rapport au centre de gravité \(G\) de la section \(x\) ;

2. Sur sa face de droite \((x + dx\)) :

   \(\overrightarrow{T}+\overrightarrow{dT}\) résultante générale des efforts exercés sur la portion de barre située à droite de la section \(x + dx\),

   \(\overrightarrow{C}+\overrightarrow{dC}\) moment résultant de ces mêmes efforts par rapport au centre de gravité \(G'\) de la même section \(x + dx\) ;

3. Dans son ensemble, \(Y(x)~dx\) effort extérieur (poids par exemple).

L’équilibre de la tranche \(dx\) exige que la résultante générale et le moment résultant de ces divers efforts soient tous nuls, soit :

Résultante nulle : \[Y~dx+T+dT-T=0\quad\text{soit}\quad Y=-\frac{dT}{dx}\]

Moment nul / G’ : \[Y~dx+C+dC-C=0\quad\text{soit}\quad T=-\frac{dC}{dx}\]

On voit en effet que le moment de \([-T]\) par rapport à \(G'\) est signe de \([T]\).

Désignant alors par \(y\) le déplacement vertical du point d’abscisse \(x\) de la fibre neutre, il vient, si la courbure est partout très faible (rayon de courbure grand devant la longueur totale de la barre) : \[C=E~I~\frac{d\alpha}{dx}=E~I~\frac{d^2y}{dx^2}\]

assimilation locale à une flexion circulaire.

Par suite : \[T=-E~I~\frac{d^3y}{dx^3}\quad;\quad Y=-E~I~\frac{d^4y}{dx^4}\]

Remarque

On pourrait penser que, sous l’action de l’effort tranchant \(T\) (soit \(T/\Sigma\) par unité de section de la barre), se produit un glissement d’ensemble de chaque petite tranche et que les génératrices de la surface de la barre s’inclinent sur les sections droites d’un angle \(\alpha\) donné par la relation : \[\frac{T}{\Sigma}=\mu~\alpha\]

Il n’en est rien : nous voyons ainsi la nécessité de considérer l’ensemble des efforts appliqués sur une section et non pas seulement leur résultante générale et leur moment résultant. Les efforts tranchants ne sont, en effet, nullement uniformes sur l’ensemble de la section \(\Sigma\).

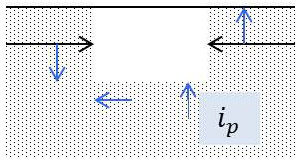Considérons uniquement ce qui se passe au voisinage du plan de symétrie (plan de la figure). Soit un parallélépipède rectangle (avant déformation) dont la face supérieure est à l’air libre. Cette face supérieure ne subit donc aucun effort normal ou tangentiel ; la continuité des tensions dans la barre exige que la face opposée du parallélépipède ne subisse que des efforts normaux ou tangentiels infiniment petits du 3° ordre.

Le couple total, perpendiculaire au plan de la figure, auquel est soumis le parallélépipède étant nul, il en résulte, puisque les efforts normaux sur les autres faces ne créent que des couples infiniment petits de 4° ordre, que les efforts tangentiels sur les faces de droite et de gauche n’ont à équilibrer que des couples du 4° ordre et sont donc des infiniment petits du 3° ordre. Le parallélépipède n’est donc soumis, dans le plan de figure, qu’à des efforts tangentiels par unité de surface infiniment petits du 1° ordre, d’où un glissement nul dans le plan de figure.

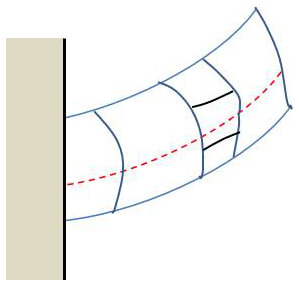Par contre, les efforts tangentiels sont importants au centre de la barre, là où précisément sont faibles les efforts normaux sur les faces de droite et de gauche. Il y a donc en définitive déformation des sections droites, dans le plan de figure, mais elles coupent toujours perpendiculairement les génératrices extérieures de la barre (voir figure ci-contre).

Cette remarque nous permettra par exemple d’affirmer, dans le cas des verges vibrantes, que le fait d’encastrer la verge à gauche entraîne les conditions aux limites : \[x=0\qquad\text{alors :}\quad y=0\quad\text{et}\quad\frac{dy}{dx}=0\]

La seconde condition ne serait pas vérifiée si un glissement apparaissait, l’effort tranchant étant particulièrement important dans le mode de vibration fondamental au point ou la verge est encastrée. En somme, les efforts tranchants ne font pas tourner (tout au moins par un effet direct de cisaillement) les génératrices, ni les diverses fibres, mais, vers le centre de la barre, ils font tourner les sections droites par rapport aux fibres pour assurer le glissement.

1.3. Applications : calculs de flèches

1.3.1. Poutre encastrée à l’origine x = 0 et chargée à l’extrémité x = L

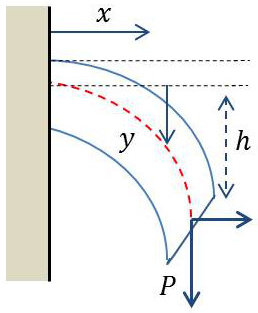Soit P la charge appliquée. Supposons négligeable le poids de la poutre. L’effort tranchant est en chaque section égal à \(T=-P\) (les efforts comme les ordonnées étant comptés positivement vers le haut). Nous écrirons donc : \[E~I~\frac{d^3y}{dy^3}=P=cte\]

Par ailleurs, le moment fléchissant pour \(x = 0\) est, si \(L\) est la longueur de la poutre : \[C_{x=0}=-P~L=E~I~\Big(\frac{d^2y}{dx^2}\Big)_{x=0}\]

L’intégration de la première équation donne : \[\frac{d^2y}{dx^2}=x~\frac{P}{E~I}+ cte\]

La valeur de la constante étant \(-L~P/E~I\) d’après la deuxième équation.

Soit en tout point : \[\frac{d^2y}{dx^2}=\frac{P}{E~I}~(x-L)\]

En intégrant deux fois et en remarquant que \(y\) et \(dy/dx\) sont nuls pour \(x = 0\) (poutre encastrée), il vient : \[y=\frac{P}{E~I}~\Big(\frac{x^2}{6}-\frac{L~x^2}{2}\Big)\]

Soit une flèche à l’extrémité L égale à : \[y(L)=h=\frac{P~L^3}{3~E~I}\]

1.3.2. Même poutre posée à ses extrémités et portant la même charge en son milieu

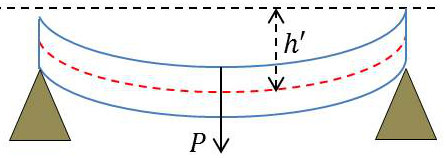La figure montre que la flèche est la même que celle d’une poutre encastrée deux fois plus courte et deux fois moins chargée. Soit une flèche 16 fois plus faible que précédemment : \[h'=\frac{P~L^3}{48~E~I}\]

2. Torsion d’un fil cylindrique

Nous considérons maintenant, au contraire, le cas où \(\overrightarrow{R}\) est partout nul et où \(\overrightarrow{C}\) se réduit à sa composante longitudinale.

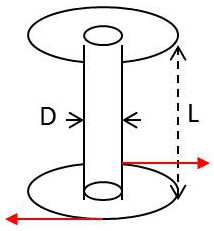Soit un fil cylindrique, à section droite circulaire, de longueur L et de diamètre D. Il se termine par deux sections droites que nous supposons, pour simplifier, soudées sur toute leur surface à des armatures indéformables.

L’armature supérieure étant immobilisée, nous faisons tourner l’armature inférieure d’un angle \(\theta\) autour de l’axe du fil. Cherchons la valeur du couple \(\Gamma\) nécessaire pour cette déformation. Le fil et les efforts appliqués présentant la symétrie de révolution autour de l’axe, les sections droites restent planes, après déformation.

Les diverses fibres se transforment en hélices de pas commun : \[h=2\pi~\frac{L}{\theta}\]

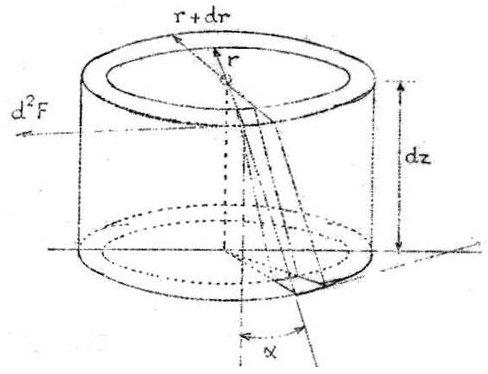Une fibre située à la distance \(r\) de l’axe coupe donc les génératrices du cylindre sur lequel elle s’enroule sous un angle : \[\alpha=2\pi~\frac{r}{h}=r~\frac{\theta}{L}\]

Les efforts tranchants appliqués en une section quelconque par la partie inférieure du fil sur sa partie supérieure sont en effet toujours les mêmes puisqu’ils doivent équilibrer le couple résistant \([-\Gamma]\) exercé à la partie supérieure.

Considérons alors une tranche de fil comprise entre deux sections distantes de \(dz\). La déformation subie par une fibre située à la distance \(r\) de l’axe est un glissement qui a fait tourner ses génératrices d’un angle \(\alpha=r~\theta/L\) par rapport à la base. Ce glissement a nécessairement un effort tangentiel : \[d^2F=\mu~dS~r~\frac{\theta}{L}\]

dont le couple par rapport à l’axe est : \[d^2\Gamma=\mu~dS~r^2~\frac{\theta}{L}\]

Intégrons sur toutes les fibres comprises entre les rayons \(r\) et \(r + dr\) : \[d\Gamma=2\pi~\mu~\frac{\theta}{L}~r^3~dr\]

Intégrons une seconde fois, de la fibre axiale aux fibres latérales : \[\Gamma=2\pi~\frac{\mu~\theta}{L}\int_0^{D/2} r^3~dr=\Big(\frac{\pi~\mu}{32}~\frac{D^4}{L}\Big)~\theta=C~\theta\]

On peut également écrire : \[C=\gamma~\frac{D^4}{L}\qquad\text{avec :}\quad \gamma=\frac{\pi~\mu}{32}\qquad\text{(loi de Coulomb)}\]

Rappelons que le module de rigidité est: \[\mu=\frac{E}{2~(L+\sigma)}\]

Les valeurs de \(\sigma\) s’échelonnant entre \(0,2~\mu m\) et \(0,4~\mu m\), soit de l’ordre de \(0,4~E\). Le coefficient de Coulomb \(\gamma\) est de l’ordre de \(\mu/L~C\).