1. Projectiles et fentes de Young

Dans le cadre de l’optique physique, une source lumineuse émettant une vibration, le dispositif expérimental des fentes de Young a permis de mettre en évidence le phénomène des interférences à partir de deux sources (secondaires) issues d’une même source (primaire).

Ce même principe va nous permettre de comprendre le comportement quantique de l’électron, à la fois onde et corpuscule.

Imaginons l’expérience suivante simulée sur ordinateur :

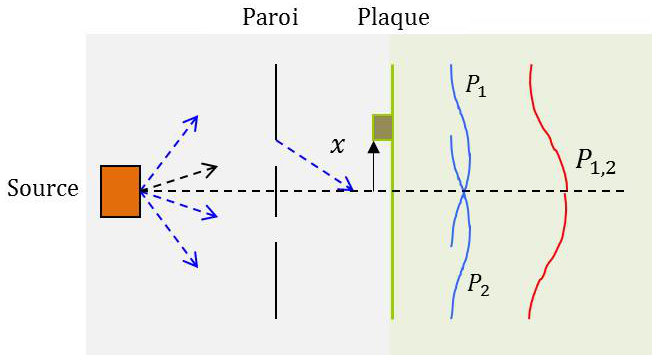Une source projette aléatoirement des particules microscopiques vers une paroi dans laquelle deux trous ont été pratiqués pour permettre à certaines balles de passer. Ces projectiles sont supposés rigoureusement identiques et indéformables, donc indiscernables. Ils sont supposés tous quitter la source exactement au même instant.

Les projectiles parviennent simultanément sur la plaque après la paroi. Un détecteur permet de les comptabiliser en différentes distances (variable \(x\)) de l’axe du système. On perçoit intuitivement un calcul classique de probabilités. Cette probabilité est la chance pour une particule d’être reçue par le détecteur à une distance \(x\) donnée. Elle peut se mesurer au rapport du nombre \(n\) de projectiles, arrivant au détecteur pendant un certain intervalle de temps, au nombre total \(N\) qui atteint la plaque dans ce même temps.

Désignons par \(P_{12}\) ou \(P_{21}\) la probabilité obtenue dans une expérience dans laquelle les projectiles peuvent passer par l’un des deux trous. Désignons par \(P_1\) et \(P_2\) la probabilité correspondant au passage par un trou unique, l’autre étant obstrué.

Dans le premier cas (voir la figure), la probabilité est maximale au centre du dispositif. Dans le deuxième cas du passage le maximum est obtenu à hauteur du trou accessible. Avec un peu de sens physique, ces deux résultats étaient intuitivement prévisibles.

Cependant, la mesure permet surtout de constater que : \[P_{12}=P_1+P_2\]

Autrement dit, l’effet obtenu avec les deux trous ouverts est égal à la somme des effets obtenus séparément avec un seul trou ouvert. Il n’y a donc pas de phénomène d’interférences.

2. Ondes et fentes de Young

Reprenons cette fois un sispositif semblable, mais cette fois la source (primaire) émet une onde que l’on peut supposer circulaire vers les deux trous (sources secondaires). Le premier exemple pratique et le plus élémentaire est celui des ondes émises par le battement périodique d’une pointe à la surface d’une cuve à eau en un point donné de la surface de l’eau.

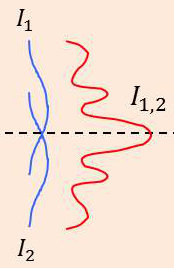
Les ondes secondaires issues des orifices se superposent. Elles s’additionnent alors soit de manière constructive soit de manière destructive selon le déphasage qui peut exister entre ces deux ondes. C’est le cas des interférences lumineuses.

Le carré \(|A|^2\) de l’amplitude de l’onde représentant son intensité \(I\), on sait que : \[\begin{aligned} I_1&=|A_1|^2\quad;\quad I_2=|A_2|^2\\ I_{12}&=|A_1+A_2|^2 \end{aligned}\]

C’est-à-dire que l’on peut poser : \[I_{12}=I_1+I_2+2~\cos\phi~\sqrt{I_1~I_2}\]

Le dernier terme est précisément celui qui caractérise le phénomène d’interférence.

En l’absence de ce terme, nous aurions : \[I_{12}=I_1+I_2\]

Le phénomène est comparable à celui de l’éclairement uniforme obtenu à partir d’un plafond garni d’un nombre d’ampoules plus ou moins important. C’est le problème dit de la cohérence pour un ensemble de sources indépendantes.

3. Électrons et fentes de Young

Reprenons le même dispositif, mais cette fois avec un canon à électrons et en modifiant la méthode d’évaluation du nombre d’électrons pour des questions d’ordre pratique.

Un multiplicateur d’électrons relié à un haut parleur fait office de détecteur réagissant encore par des clics sonores correspondant aux arrivées des électrons. Tous ces clics sont identiques et nets, c’est-à-dire subissant sans distinction les mêmes effets et réagissant de manière binaire.

Tous les clics sont comptabilisés pendant un laps de temps significatif. La mesure est faite une deuxième fois, pendant un autre intervalle de temps identique au précédent. Les deux nombres obtenus sont très proches. Il s’agit bien d’un rythme moyen de clics pendant le laps de temps choisi.

À la suite de diverses expériences de ce type, et avec plusieurs détecteurs, on peut établir que les électrons arrivent en paquets, tous de même taille. Ce sont seulement des paquets entiers qui arrivent d’un seul coup sur la plaque.

En comptabilisant cette fois des flux \(\Phi\) d’électrons, nous retrouvons le résultat obtenu pour des ondes (calcul des probabilités) : \[\begin{aligned} P_1&=|\Phi_1|^2\quad;\quad P_2=|\Phi_2|^2\\ P_{12}&=|\Phi_1+\Phi_2|^2 \end{aligned}\]

On a donc : \[P_{12}\neq P_1+P_2\]

Il s’est donc produit un phénomène d’interférences.

4. Photons et fentes de Young

Utilisons à présent une source lumineuse et une plaque photographique. Si l’intensité de la source lumineuse est forte, le résultat est analogue à celui obtenu avec les ondes précédentes : nous obtenons des interférences d’ondes lumineuses, c’est-à-dire des franges sombres en alternance avec des franges éclairées.

Si l’on diminue l’intensité de la source lumineuse au moyen de filtres absorbants, on constate que l’intensité lumineuse sur la plaque résulte cette fois d’une multitude d’impacts lumineux microscopiques.

Ce résultat était prévisible. Le flux lumineux est en réalité discontinu, c’est-à-dire constitué d’identités individuelles : les photons. Ceux-ci arrivent donc un par un sur la plaque. Ils sont alors dénombrables au même titre que les particules classiques.

Néanmoins, cet aspect corpusculaire n’empêche pas l’apparition des phénomènes d’interférences comme dans le cas des ondes classiques.

Ceci est un point important quand on veut ressentir et expliquer la mécanique quantique par l’expérience. C’est le nombre plus ou moins grand de photons arrivant sur une zone donnée de la plaque qui rend compte de ces différences d’éclairement et par suite de l’apparition d’interférences.

5. Interprétations. Ouverture sur le quantique

5.1. Des points d’impact

Il faut à présent s’imprégner de l’idée que l’apparition du phénomène d’interférences ondulatoire ne fait que traduire une répartition des impacts successifs des particules. Photons et électrons ne sont donc assimilables ni aux corpuscules, ni aux ondes de la mécanique classique.

Il en est ainsi de toutes les particules de la microphysique, qui présentent des caractères à la fois spécifiques et universels. Et pour être encore plus rigoureux, nous dirons que tous les micro-objets se comportent de même.

Les concepts séparatistes de corpuscule et d’onde ne sont que deux approximations, qui sont tout à fait valables à l’échelle macroscopique et cependant incompatibles entre elles.

Quand il sera question de particules quantiques, on saura qu’il ne s’agit ni de corpuscules, ni d’ondes, chacune des images pouvant être utile dans certaines conditions, ce qui reste par contre très pratique. Et l’un des buts de la mécanique quantique, fondamental, consistera à formaliser de façon cohérente ce comportement avec la rigueur de l’outil mathématique.

L’existence même du phénomène d’interférences amène à introduire, comme dans le cas des ondes classiques, des amplitudes capables de s’ajouter.

Dans le cas ondulatoire classique des intensités étaient associées aux carrés de ces amplitudes. Ici, il ne peut être question ici d’intensités continues du fait qu’il s’agit d’impacts individuels, discrets des particules.

5.2. Des probabilités

C’est Max Born qui eut cette idée géniale d’interpréter ces quantités comme des probabilités d’arrivée des particules (1924). De ce fait, le processus quantique quelconque peut être décrit en termes d’amplitudes de probabilité. Le carré de ces amplitudes correspond plus précisément à la densité de probabilité de réalisation de l’état final considéré à partir de l’état initial.

La propriété essentielle de ces amplitudes de probabilité réside dans leur additivité. Pour un état initial et un état final déterminés, l’amplitude correspond à la conjonction de plusieurs éventualités intermédiaires. Ainsi, dans l’expérience des fentes de Young (ouverture de un ou deux trous par exemple), on effectue la somme des amplitudes correspondant à chaque éventualité.

Toutefois, ce principe de superposition des amplitudes exclut l’additivité des probabilités en tant que telles et il est à la base des effets les plus notables de la mécanique quantique. La double apparence (classique-quantique) des particules se traduit par deux formules fondamentales qui relient entre eux leurs aspects corpusculaires et ondulatoires.

5.3. Un point commun : fréquence-énergie

Comme les corpuscules classiques, les particules quantiques sont caractérisées par leur énergie \(E\) et par leur quantité de mouvement \(p\). Comme les ondes classiques, elles peuvent être décrites à l’aide de leur fréquence temporelle \(\nu=1/T\) et de leur fréquence spatiale, ou nombre d’ondes \(k=1/\lambda\).

On doit à Planck et à Einstein d’une part (1900-1905) et à de Broglie de l’autre (1924) d’avoir établi la proportionnalité de ces grandeurs suivant les relations : \[\left\{ \begin{aligned} E&=h~\nu\\ p&=h~k=h~\frac{1}{\lambda} \end{aligned} \right. \qquad~~h\text{ : constante de Planck}~(h=6,6\times 10^{-34}~\rm J~s)\]

Une application bien connue est celle de l’effet photoélectrique. Einstein a montré (1905) que l’impact d’un photon de fréquence \(\nu\) sur un métal suffisait à en extraire un électron sous cette condition que l’énergie \(h~\nu\) du photon soit supérieure à l’énergie d’extraction \(W\), nécessaire pour dégager l’électron du métal. L’électron émerge alors avec l’énergie : \[E'=h~\nu-W\]