1. Approximation de Gauss

En optique géométrique, l’approximation de Gauss correspond à des angles d’incidence des rayons faibles. Ce qui signifie qu’ils suivent une direction proche de la normale de la surface de séparation de l’instrument d’optique. Le point d’incidence est alors proche de l’axe optique. On dit que l’on travaille avec des rayons paraxiaux.

On obtient dans ces conditions un stigmatisme approché. Les écarts à cette approximation (rencontrés notamment dans les instruments d’optique travaillant en grand angle) sont appelés aberrations géométriques.

Nous limiterons notre étude aux rayons qui, en cheminant à travers le système, rencontrent toutes les surfaces sous une faible incidence et proviennent de points objets voisins de l’axe, c’est-à-dire aux rayons qui restent constamment à faible distance de l’axe. C’est l’approximation de Gauss.

En ce qui concerne le tracé des rayons, nous adopterons les conventions classiques de signes en matière d’axes de coordonnées et d’orientation angulaire.

2. Miroirs sphériques en approximation de Gauss

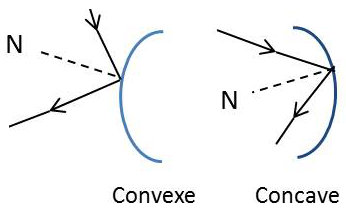Les miroirs sphériques sont des miroirs dont la surface réfléchissante est une portion de sphère.

Si cette surface réfléchissante est tournée vers le centre, le miroir est dit concave. Il est convexe dans le cas contraire.

Le pôle S de la calotte sphérique s’appelle le sommet du miroir.

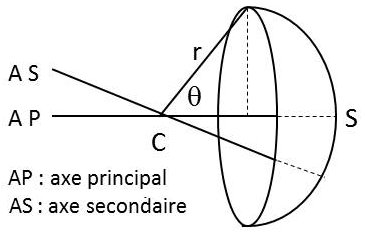L’axe CS qui contient le centre et le sommet du miroir est l’axe principal du miroir.

Toute autre droite passant par C et rencontrant la surface réfléchissante est un axe secondaire.

Tout plan passant par l’axe principal est une section principale.

Le rayon d’ouverture du miroir est le rayon du cercle de base de la calotte.

L’angle d’ouverture est le demi angle au sommet, \(\theta\), du cône de sommet C ayant le contour du miroir pour directrice.

2.1. Étude du stigmatisme

2.1.1. Recherche directe

Soit A un point lumineux situé en avant d’un miroir supposé concave. Le rayon AC tombe normalement sur le miroir en S et se réfléchit sur lui-même. SC est un premier rayon réfléchi.

Prenons dans le plan de la figure un deuxième rayon incident AI.

La normale en I au miroir est IC ; elle est dans le plan de la figure ; celui-ci est donc le plan d’incidence et d’après la première loi de Descartes, il contient le rayon réfléchi.

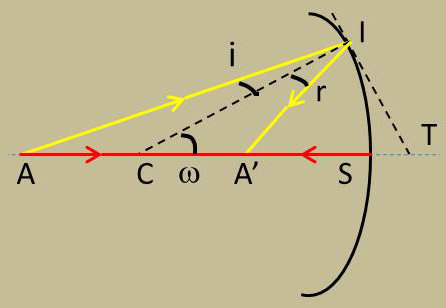L’angle de ce rayon réfléchi, dans le plan de la figure, est donné par la deuxième loi de Descartes : \[\widehat r~~=-\widehat i\]

Les deux rayons réfléchis, l’un en S et l’autre en I, sont dans le même plan et se coupent en A’.

Voyons si le point A’ reste fixe sur l’axe ACS quand on fait varier le rayon incident AI. IC est naturellement une bissectrice intérieure de l’angle \(\widehat{I}\).

Menons la tangente en I à la trace du miroir. Elle coupe en T le diamètre ACS. Comme elle est perpendiculaire en I à IC, elle est bissectrice extérieure de l’angle \(\widehat{I}\).

Les quatre demi-droites IA, IC, IA’, IT forment donc un faisceau harmonique. Leurs points d’intersection A, C, A’, T déterminent sur cette droite une division harmonique.

A et C sont des points fixes.

Si T était fixe, A’ le serait aussi et il y aurait stigmatisme.

La position de T dépend de celle de I. T s’éloigne de S sur CS à mesure que I s’écarte de S.

Le miroir sphérique n’est donc pas stigmatique pour un point quelconque.

Du fait de la division harmonique : \[\frac{1}{\overline{CA}}~+~\frac{1}{\overline{CA'}}~=~\frac{2}{\overline{CT}}~=~\frac{2\cos\omega}{\overline{CS}}\]

Posons : \[\overline{CA}~=~z\qquad \overline{CA'}~=~z'\qquad \overline{CS}~=~\rho ~= -r\]

Tous calculs faits : \[z'~=~z~\frac{\rho}{2z~\cos\omega -\rho }\]

Nous voyons que, en général, z’ dépend non seulement de z et \(\rho\), mais aussi de \(\omega\). Nous retrouvons le résultat indiqué : il n’y a pas de stigmatisme pour un point quelconque.

2.1.2. Stigmatisme rigoureux

Si \(\omega\) est constant, ce qui ne peut avoir lieu que si A est sur la surface. On a alors :

\[\begin{aligned} \omega~=~0 \qquad &\Rightarrow \qquad \cos \omega~=~1\\ z=\rho \qquad &\Rightarrow \qquad z'~=~\rho\end{aligned}\]

Nous retrouvons un résultat évident a priori. Il y a stigmatisme pour tout point lumineux situé sur la surface réfléchissante, qui est à lui-même son image.

2.1.3. Stigmatisme approché

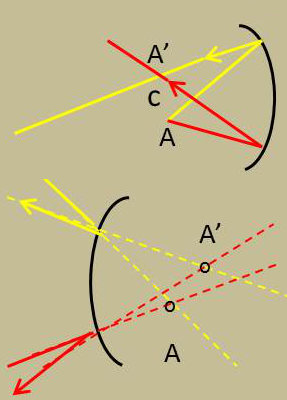Les positions de stigmatisme approché peuvent d’abord être recherchées au voisinage des positions de stigmatisme rigoureux. Nous sommes conduits à voir ce qui se passe si le point A est voisin du centre.

Supposons \(z\) infiniment petit du premier ordre : \(z=\varepsilon\ll\rho\).

Alors, en négligeant les infiniment petits d’ordre supérieur : \[z'~=~z~\frac{\rho}{2\frac{z}{\rho}\cos\omega -1 }\]

Ou, en passant au développement limité : \[z'=-\varepsilon~(1+\frac{2\varepsilon}{\rho}\cos\omega-\frac{4\varepsilon^2}{\rho^2}\cos^2\omega+\cdots)\approx -\varepsilon\]

Tous les rayons issus de A iront donc passer, après réflexion, à un infiniment petit du deuxième ordre près par un point A’ symétrique de A par rapport au centre C.

Si \(\omega\) reste toujours très petit, nous pouvons dans le développement en série de négliger les puissances de \(\omega\) d’ordre supérieur à 1 et poser \(\cos\omega=1\) .

Il revient au même de dire qu’une fonction \(\cos\omega\) garde sa valeur maximum au voisinage immédiat de ce maximum. La relation harmonique s’écrit alors: \[\frac{1}{z}~+~\frac{1}{z'}~=~\frac{2}{\rho}\] On remarque que \(\omega\) ne figure plus dans l’expression : z’ est déterminé pour toute valeur de z.

Il y a donc stigmatisme approché pour tout point A de l’espace qui n’envoie sur le miroir qu’un pinceau lumineux dont le rayon moyen est normal à la surface réfléchissante. Dans ces conditions, l’image A’ de A est sur l’axe AC et sa position sur l’axe est donnée par la relation harmonique précédente.

3. Miroir sphérique de faible ouverture

Nous faisons toujours l’approximation de Gauss.

3.1. Miroir de faible ouverture. Point objet sur l’axe principal.

Reprenons la relation : \[\frac{1}{z}~+~\frac{1}{z'}~=~\frac{2}{\rho}\]

Prenons comme origine S. On pose : \[\overline{SA}=x\qquad \overline{SA'}=x' \qquad \overline{SC}=r\]

On a alors : \[\frac{1}{x}~+~\frac{1}{x'}~=~\frac{2}{r}\]

C’est l’équation aux points conjugués ou équation de conjugaison.

Nous poserons désormais \(f~=~r/2\).

D’où la relation définitive : \[\frac{1}{x}~+~\frac{1}{x'}~=~\frac{1}{f}\]

Points cardinaux

1) Tout rayon incident qui passe par le centre se réfléchit sur lui-même : \[x~=~r \qquad \Rightarrow \qquad x'~=~r'\]

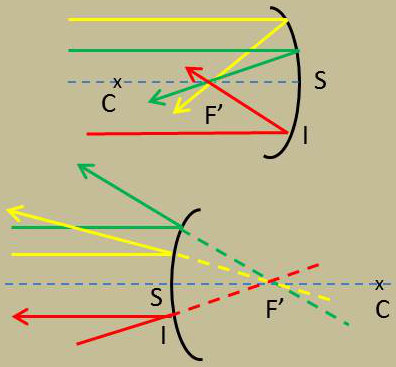2) Lorsque le point A est situé à l’infini sur l’axe, son image est au milieu F’ du segment SC : \[x~=~\infty \qquad \Rightarrow \qquad x'~=~f~=~r/2\]

Ce point F’ s’appelle le foyer image du miroir. Il est réel si le miroir est concave, virtuel s’il est convexe.

On voit aussi que le paramètre \(f\) caractérise la distance entre le sommet du miroir et le foyer image F’ ; cette distance s’appellera la distance focale du miroir.

Tout incident parallèle à l’axe donne donc un réfléchi qui passe par F’, réellement si le miroir est concave, virtuellement si le miroir est convexe.

Un miroir sphérique recevant un faisceau lumineux parallèle à son axe principal le transformera en un faisceau convergent s’il est concave et un faisceau divergent s’il est convexe.

Nous appellerons foyer objet, la position particulière F que doit occuper le point A sur l’axe pour que le point image A’ soit à l’infini.

La relation harmonique 2) lorsque nous faisons \(x~=~\infty\) montre que le point F est au milieu de SC.

Le foyer objet et le foyer image sont donc confondus.

Tout rayon incident dont le support passe par F est réfléchi parallèlement à l’axe. Tout miroir sphérique possède sur son axe principal un foyer image et un foyer objet confondus avec le milieu de \(SC\).

Ils sont simultanément réels si le miroir est concave et simultanément virtuels si le miroir est convexe.

3.2. Miroir de faible ouverture. Point objet très proche de l’axe principal

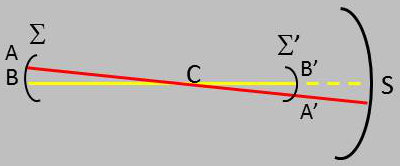Le point B est pris en dehors de l’axe du miroir de faible ouverture, mais assez près de l’axe pour que tous les rayons tombent sur le miroir sous une faible incidence.

Le miroir donne de B une image satisfaisante située sur l’axe secondaire BC et dont la position, sur cet axe, est définie par la relation harmonique fondamentale.

Si donc le point B décrit une calotte sphérique de centre C, le point B’ décrit une calotte sphérique de centre C, homothétique de \(\Sigma\) par rapport à C.

Autrement dit, \(\Sigma'\) sera l’image que le miroir de faible ouverture donne de \(\Sigma\) .

Mais B restant très proche de l’axe principal, les deux calottes sphériques doivent être très limitées au voisinage immédiat de l’axe et on peut les confondre avec une portion de leur plans tangents P et P’ aux points A et A’ où l’axe les perce.

Dans l’approximation de Gauss, un miroir sphérique de faible ouverture donne donc d’un objet plan, perpendiculaire à son axe et centré sur lui, une image plane, perpendiculaire à l’axe et centrée sur lui.

Le plan de front objet P et le plan de front image P’ sont dits plans conjugués. Ils rencontrent l’axe principal du miroir en deux points conjugués A et A’ dont les positions sont liées par la relation harmonique. L’image est homothétique de l’objet par rapport au centre C du miroir.

4. Plans focaux

Lorsque le plan objet P est à l’infini, le plan image P’ doit couper l’axe en F’ conjugué du point objet à l’infini sur l’axe. Ce plan mené par le foyer image perpendiculairement à l’axe principal du miroir porte le nom de plan focal image. Il est réel pour les miroirs concaves et il est virtuel pour les miroirs convexes.

Inversement, si le plan P coupe l’axe en F, foyer objet, il s’appelle plan focal objet. Son image est un plan perpendiculaire à l’axe. Il est confondu avec le plan focal image, réel si le miroir est concave, virtuel si le miroir est convexe.

5. Construction de l’image d’un objet plan perpendiculaire à l’axe

5.1. Le plan objet est à l’infini.

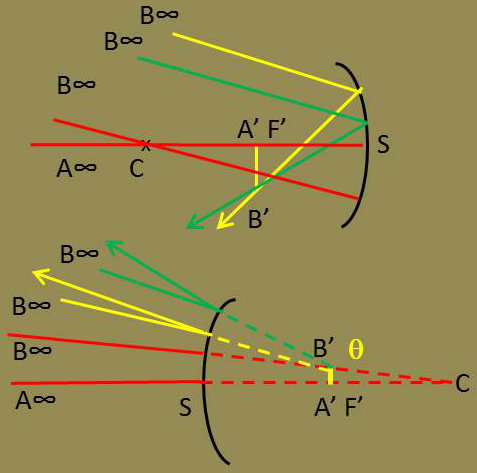Quand le plan objet est à l’infini, son image est dans le plan focal donc le point A sur l’axe a son image en F’.

Un point B en dehors de l’axe et dont la distance angulaire au point A est \(\theta\) très petite a son image B’ au point d’intersection du plan focal et de l’axe secondaire BC.

Si le miroir est concave, l’image est réelle et renversée.

Le calcul de A’B’ est élémentaire : \[A'B'\approx CA'.\theta~=~-f.\theta\]

Sur la figure, nous avons représenté la marche d’un pinceau de rayons issus de B (pinceau incident parallèle à BC). Tous les rayons réfléchis vont passer par B’ image de B.

Si le miroir est convexe, l’image est virtuelle. Nous la représentons en pointillé. L’image est orientée cette fois dans le même sens que l’objet (pas de renversement). On dit que l’image est droite. Nous aurons comme précédemment : \[A'B'~=~-f.\theta \qquad (r<0)\]

5.2. Le plan objet est dans le plan focal.

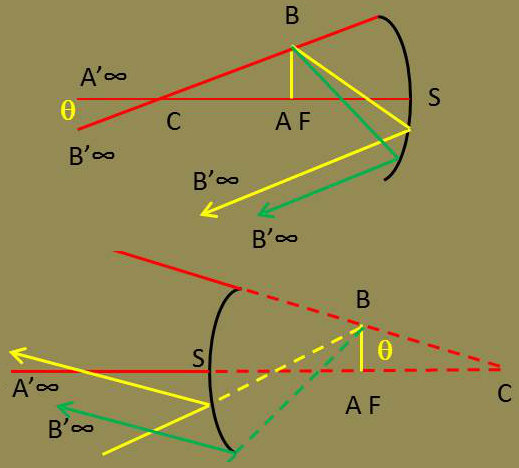Quand le plan objet est à l’infini, son image est à l’infini. Le point A sur l’axe a son image à l’infini sur cet axe.

Un point B en dehors de l’axe a son image à l’infini dans la direction BC. Le diamètre apparent de l’image A’B’ est donné par la relation : \[\theta~=~\frac{2~AB}{CS}~=~\frac{AB}{-f}\]

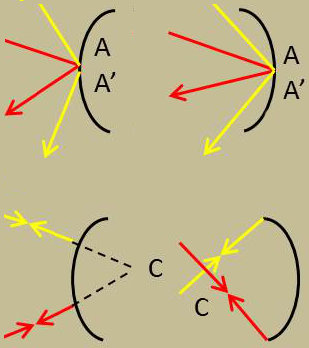
Les figures ci-contre précisent la nature et l’orientation de l’image. Elles donnent la marche d’un pinceau de rayons correspondant au point B.

Si le miroir est concave, l’objet AB est réel ; un pinceau issu de B est réfléchi parallèlement à BC.

Si le miroir est convexe, l’objet est virtuel ; un pinceau de rayons qui irait passer par B en l’absence du miroir est réfléchi parallèlement à la direction BC.

5.3. La position de l’objet est quelconque.

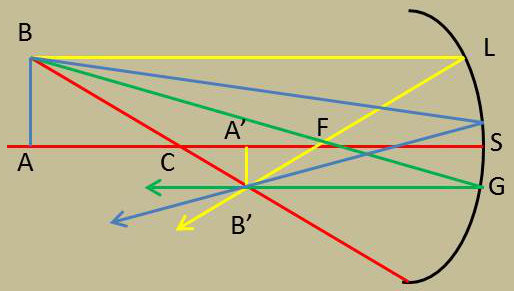Pour expliquer la construction quand la position de l’objet est quelconque, supposons par exemple le miroir concave et l’objet réel placé en avant du centre.

Considérons dans le plan objet P un point B situé en dehors de l’axe SC. Il nous suffit évidemment de construire l’image B’ de B. Le plan P’ mené par B’ perpendiculairement à l’axe sera l’image de P.

Le point B’ étant l’image de B est le point d’intersection de tous les rayons réfléchis correspondant aux rayons incidents issus de B. Deux réfléchis et par suite deux incidents suffisent pour le déterminer.

Nous prendrons les incidents tels que nous sachions tracer sans peine les réfléchis qui leur correspondent. Nous avons le choix entre deux quelconques des quatre incidents suivants :

1. Le rayon BS qui se réfléchit symétriquement par rapport à l’axe.

2. Le rayon BCI passant par le centre qui se réfléchit en revenant sur lui-même (axe secondaire passant par B).

3. Le rayon BL parallèle à l’axe principal qui se réfléchit en passant par le foyer.

4. Le rayon BFG passant par le foyer qui se réfléchit parallèlement à l’axe principal.

Les rayons réfléchis considérés se coupent en B’. Abaissons de B’ la perpendiculaire B’A’ sur l’axe. B’A’ est l’image de la dimension AB de l’objet. Nous constatons que, dans le cas de la figure envisagée, l’image est réelle, renversée et plus petite que l’objet.

À titre d’exercice et pour préciser la façon dont il convient de s’exprimer quand l’objet est virtuel, faisons la construction lorsque, le miroir étant par exemple convexe, l’objet virtuel est placé entre le foyer et le sommet.

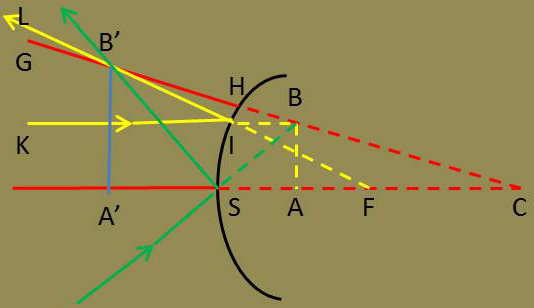Soit A le point sur l’axe et B le point en dehors de l’axe. Parmi les rayons incidents qui iraient passer en B si le miroir n’existait pas, considérons :

1. Le rayon GH qui tombe normalement sur le miroir (son prolongement passe par B et C) ; il se réfléchit en revenant sur lui-même.

2. Le rayon KI parallèle à l’axe ; il se réfléchit suivant IL en passant virtuellement par le foyer F’.

Les rayons réfléchis HG et IL se coupent en B’. B’ est l’image réelle de B et B’A’ menée perpendiculairement à l’axe est l’image de la dimension BA du plan objet.

Nous voyons que le miroir convexe donne d’un objet virtuel placé entre son sommet et son foyer, une image droite, réelle et agrandie.

6. Grandissement linéaire

On appelle grandissement linéaire le rapport : \[\gamma=\frac{\overline{A'B'}}{AB}\]

Le signe de ce rapport fixe l’orientation de l’image par rapport à l’objet. S’il est positif l’image est droite. S’il est négatif l’image est renversée.

Ce rapport dépend naturellement de la position de l’objet. Pour l’évaluer, nous considérons les triangles semblables ABS et A’B’S. Ils nous donnent en grandeur et en signe : \[\frac{\overline{A'B'}}{AB}=-\frac{\overline{SA'}}{SA} \qquad \Rightarrow \qquad \gamma= -\frac{x'}{x}\]

Remarquons d’autre part que les points C, B et B’ étant alignés on peut aussi écrire :

\[\frac{\overline{A'B'}}{AB}=\frac{\overline{CA'}}{CA}\]

L’objet et l’image sont ainsi homothétiques par rapport au centre.

7. Formules de Newton. Choix de l’origine

On peut maintenant changer l’origine des coordonnées pour prendre le foyer objet (ou image). Posons alors : \[\overline{FA}~=~\sigma \qquad \overline{FA'}~=~\sigma' \qquad (\overline{SF}~=~f)\]

La formule de conjugaison peut se déduire de la relation harmonique fondamentale par un changement d’origine et application de la formule de Chasles.

Il est plus commode d’établir directement en raisonnant sur la figure (construction géométrique de l’image) les relations de conjugaison et de grandissement.

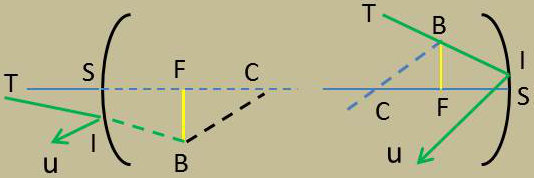
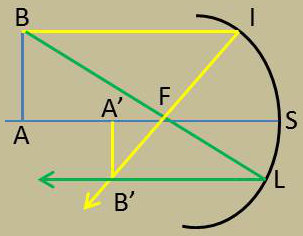Puisque nous sommes dans les conditions de l’approximation de Gauss, nous pouvons confondre les arcs IS et LS avec des droites perpendiculaires en S à CS.

La similitude des triangles A’B’F et SIF donne :

\[\frac{\overline{A'B'}}{\overline{SI}}=\frac{\overline{FA'}}{\overline{FS}} \qquad \text{ou} \qquad \frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{FA'}}{\overline{FS}}\]

C’est-à-dire : \[\gamma~=~-\frac{\sigma'}{f}\]

La similitude des triangles ABF et FSL fournit une autre expression du grandissement : \[\frac{\overline{SL}}{\overline{AB}}=\frac{\overline{FS}}{\overline{FA}} \qquad \text{ou} \qquad \frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{FS}}{\overline{FA}}\]

C’est-à-dire : \[\gamma~=~-\frac{f}{\sigma'}\]

Et en comparant ces expressions : \[\sigma~\sigma'~=~f^2\]

L’ensemble de ces trois formules constitue les formules de Newton.

Remarques

Le produit \(\sigma\sigma'\) étant toujours positif, l’image et l’objet sont toujours du même côté du foyer. Le produit \(\sigma\sigma'\) étant constant, \(\sigma'\) varie en sens inverse de \(\sigma\) : si l’objet se rapproche du foyer, l’image s’en éloigne et inversement. Objet et image se déplacent en sens contraire.

7.1. Tableau des formules de conjugaison

C’est la nature du problème à traiter qui doit guider sur l’origine qu’il convient d’adopter. On prend généralement pour origine celui des points S ou F qui présente dans le système optique donné, la position la plus importante. Rappelons ces groupes de formules :

Origine au centre : \[\frac{1}{z}+\frac{1}{z'}=\frac{2}{\overline{CS}} \quad;\quad \frac{y'}{y}=\frac{z'}{z}\]

Origine au sommet : \[\overline{SA}=x \quad;\quad \overline{SA'}=x' \quad;\quad \overline{SC}=r=2~\overline{SF}=2f\] \[\frac{1}{x}+\frac{1}{x'}=\frac{1}{f} \quad;\quad \gamma=-\frac{x'}{x}\]

Origine au foyer : \[\overline{FA}=\sigma \quad;\quad \overline{FA'}=\sigma' \quad;\quad \overline{SF}=f\] \[\sigma\sigma'=f^2 \quad;\quad \gamma=-\frac{\sigma'}{f}=-\frac{f}{\sigma}\]

Le choix de l’origine en S permet de reconnaître tout de suite la nature de l’objet ou de l’image, laquelle dépend uniquement du signe de x (pour l’objet) et de x’ (pour l’image) avec le sens positif adopté sur l’axe.

Si ce sens positif est celui de la lumière réfléchie :

• x est positif si l’objet est réel et négatif s’il est virtuel ;

• x’ est positif si l’image est réelle et négatif si l’image est virtuelle.

8. Discussion des formules

Il est intéressant de voir comment varient la position, la grandeur et l’orientation de l’image d’un objet lorsque l’on fait varier la position de l’objet par rapport au miroir. Cette discussion peut se faire à partir de l’un quelconque des deux groupes de formules précédentes (S ou F). Utilisons par exemple les formules de Descartes :

\[x'=\frac{f.x}{x-f} \quad;\quad \gamma=\frac{f}{f-x}\]

Les valeurs remarquables sont celles qui annulent les numérateurs et les dénominateurs de ces expressions : \[x=0 \quad;\quad x=f \qquad \text{ainsi que}\qquad x=\pm\infty\]

La valeur \(x=2f\) présente aussi un certain intérêt parce que l’on a dans ce cas \(\gamma =-1\).

9. Construction du réfléchi pour un incident donné

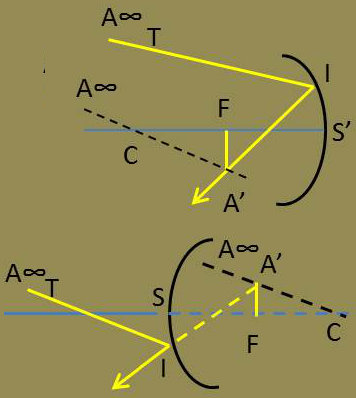Soit TI le rayon incident. Le rayon réfléchi passe par I.

Cherchons un deuxième point de ce rayon.

Nous pouvons admettre que l’incident provient d’un point A placé à l’infini sur son support. Le réfléchi passera donc par A’ image de A. Cette image s’obtient en prenant le point d’intersection A’ du plan focal et l’axe secondaire CA (parallèle à TI menée par C).

Le rayon réfléchi est IA’.

Autre construction simple

Admettons que le rayon TI soit émis par le point B où il perce le plan focal.

Le réfléchi passera par B’ image de B dans le miroir, cette image étant à l’infini sur l’axe secondaire \(BC\).

Le rayon cherché est la parallèle IU à BC menée par le point I.

10. Détermination rapide de la nature d’un miroir sphérique

L’observateur se place devant le miroir à faible distance :

• S’il se voit agrandi, le miroir est concave.

• S’il se voit rapetissé, le miroir est convexe.

• Une image en vraie grandeur serait donnée par un miroir plan.

L’observateur ne peut se placer qu’à grande distance :

• S’il se voit renversé, le miroir est concave.

• S’il se voit avec son orientation naturelle, le miroir est convexe.