1. Généralités

La lentille est dite infiniment mince lorsqu’on peut négliger son épaisseur \(e\) vis-à-vis des rayons de courbure \(R_1\) et \(R_2\) de ses faces.

Les points \(S_1\) et \(S_2\) peuvent dès lors être confondus en un point S, point où la lentille est percée par son axe.

Nous pourrions, pour avoir la position des points cardinaux, utiliser les formules générales relatives aux lentilles épaisses dans lesquelles nous ferions \(e = 0\).

Mais nous pouvons aussi faire une étude directe de la lentille en la considérant comme une succession de deux dioptres sphériques de même sommet S.

Remarquons en passant que les deux plans principaux sont confondus avec le plan de la lentille car tout rayon parallèle à l’axe rencontre dans ce plan le rayon réfracté qui lui correspond. Les deux points principaux sont en S.

2. Milieux extrêmes différents

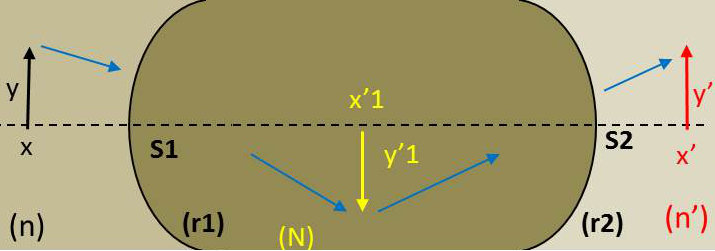Appelons n, N et n’ les indices des milieux successifs. Soit AB un objet : le dioptre \(S_1\) de rayon \(r_1\) en donne une image \(A'_1B'_1\) dont la position, la grandeur et l’orientation sont données par des relations connues, rapportées au point S pris comme origine :

\[\begin{aligned} &[1]\qquad\frac{N}{x'_1}-\frac{n}{x}=\frac{N-n}{r_1}\\ &[2]\qquad\frac{y'_1}{y}=\frac{n}{N}~\frac{x'_1}{x}\end{aligned}\]

\(A'_1B'_1\) joue le rôle d’objet par rapport au dioptre \(S_2\) de rayon \(r_2\), qui en donne une image \(A'B'\) qui est l’image de \(AB\) à travers la lentille. Les relations qui fixent la position et la grandeur de \(A'B'\) en fonction de la position et de la grandeur de \(A'_1B'_1\) sont les mêmes :

\[\begin{aligned} &[3]\qquad\frac{n'}{x'}-\frac{N}{x'_1}=\frac{n'-N}{r_2}\\ &[4]\qquad\frac{y'}{y'_1}=\frac{N}{n'}~\frac{x'}{x_1}\end{aligned}\]

En faisant membre à membre respectivement [1] + [3] et [2] x [4], il vient :

\[\begin{aligned} &[5]\qquad\frac{n'}{x'}-\frac{n}{x}=\frac{n'-N}{r_2}+\frac{N-n}{r_1}\\ &[6]\qquad\frac{y'}{y}=\frac{n'}{n}~\frac{x'}{x}\end{aligned}\]

Posons : \[[7]\qquad\frac{n'-N}{r_2}+\frac{N-n}{r_1}=\frac{n'-n}{r}\]

L’équation [5] devient : \[[8]\qquad\frac{n'}{x'}-\frac{n}{x}=\frac{n'-n}{r}\]

Les équations [6] et [8] ne sont autres que les équations de grandissement et de conjugaison relatives à un dioptre de sommet S, de rayon r et séparant un milieu objet d’indice n d’un milieu image d’indice n’, donc :

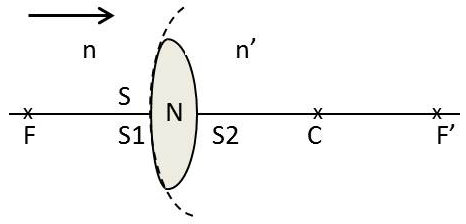Toute lentille infiniment mince S d’indice N séparant deux milieux d’indices n et n’, est équivalente à un dioptre unique placé en S, en contact avec les mêmes milieux et dont le rayon est donné par [7].

Tout ce qui a été dit pour le dioptre sphérique s’applique ici sans restriction (construction géométrique des images, formules de conjugaison, etc.).

3. Milieux extrêmes identiques

Quand les milieux extrêmes sont identiques, les points nodaux sont confondus avec les points principaux, ils sont donc en S qui est ainsi le centre optique de la lentille.

Tout rayon incident qui passe par S continue son chemin dans sa propre direction, résultat évident puisque pour ce rayon la lentille se comporte comme une lame à faces parallèles infiniment mince.

Une telle lame, non seulement ne dévie pas les rayons lumineux, mais elle ne les déplace pas. Les deux distances focales sont égales et de signes contraires.

4. Relations de conjugaison et de grandissement

Elles se déduisent immédiatement des relations [5] et [6] précédentes dans lesquelles on fait \(n=n'=1\).

Dans ces conditions N sera l’indice relatif de la lentille par rapport au milieu qui la baigne.

\[\begin{aligned} &[1]\qquad\frac{1}{x'}-\frac{1}{x}=(N-1)~\big\{\frac{1}{r_1}-\frac{1}{r_2}\big\}\\ &[2]\qquad\gamma_y=\frac{x'}{x}\end{aligned}\]

La relation [2] montre que l’objet et l’image sont homothétiques par rapport au point S, centre optique.

Le foyer objet est le point F dont l’image est à l’infini sur son axe.

Son abscisse \(\overline{SF}=f\) est la distance focale objet (abscisse du foyer objet par rapport au plan principal objet). Elle s’obtient en faisant \(x'=\infty\) dans la relation [1] : \[D=-\frac{1}{f}=(N-1)~\big\{\frac{1}{r_1}-\frac{1}{r_2}\big\}\]

Le foyer image est le point F’ de l’axe, image du point à l’infini sur cet axe.

Son abscisse \(\overline{SF'}=f'\) qui est la distance focale image, s’obtient en faisant \(x=\infty\) dans la relation [3] : \[D=\frac{1}{f'}=(N-1)~\big\{\frac{1}{r_1}-\frac{1}{r_2}\big\}\]

Les deux distances focales sont bien opposées.

Rappelons, pour mémoire, que les formules de Newton s’écrivent ici : \[\frac{y'}{y}=+\frac{f'}{\sigma}=-\frac{\sigma'}{f}\quad\Rightarrow\quad\sigma~\sigma'=f'^2\]

5. Classification des lentilles minces

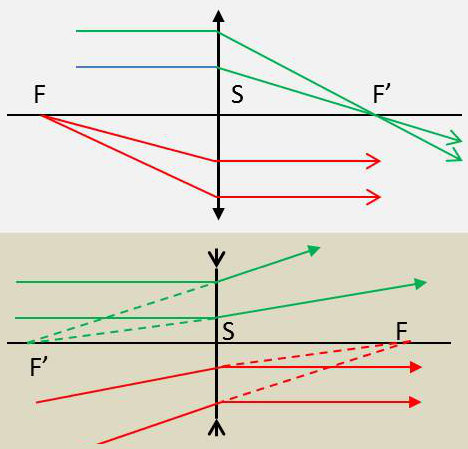Les distances focales étant opposées, les foyers sont disposés symétriquement par rapport au plan de la lentille.

Ils sont simultanément réels ou simultanément virtuels.

Si les foyers sont réels, la lentille est convergente. Quel que soit le sens dans lequel elle travaille, elle transforme un faisceau incident parallèle à son axe en un faisceau convergent.

Si les foyers sont virtuels, la lentille est divergente. Elle transforme un faisceau cylindrique parallèle à son axe en un faisceau divergent.

Avec les conventions de signe habituelles, la lentille est convergente si la distance focale \(f'=\overline{H'F'}>0\). Elle est divergente si \(f'<0\).

Le signe de \(f'\) est fonction de la forme de la lentille et de son indice.

Nous allons faire la discussion en supposant, ce qui est généralement le cas, que \(N>0\). Le signe de \(f'\) est alors celui de l’expression : \[A=\frac{1}{r_1}-\frac{1}{r_2}\] Montrons que le signe de A détermine le signe de la différence d’épaisseur entre le centre et le bord de la lentille.

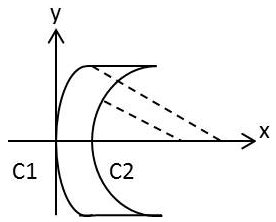Par rapport à des axes x et y l’équation du premier dioptre sera, en ne prenant que les termes en y² : \[x_1=\frac{y^2}{2~r_1}\]

De même, si \(e_0\) est l’épaisseur au centre, l’équation du second dioptre sera : \[x_2=e_0+\frac{y^2}{2~r_2}\]

Si l’on appelle h son rayon, l’épaisseur au bord de la lentille sera : \[e=x_2-x_1=e_0+\frac{h^2}{2}~\big\{\frac{1}{r_2}-\frac{1}{r_1}\big\}\]

Ou encore : \[e-e_0=-\frac{h^2}{2}~A=-\frac{h^2}{2~(N-1)}~D\]

Les lentilles convergentes sont celles pour lesquelles \(A>0\) et \(e-e_0<0\), c’est-à-dire les lentilles à bords minces. Inversement les lentilles divergentes sont les lentilles à bord épais.

Remarques

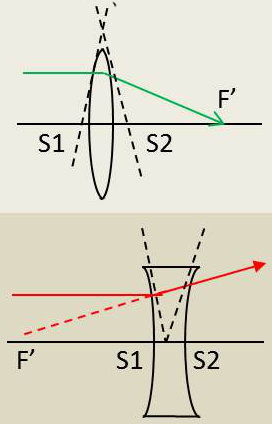Ces résultats se retrouvent sans difficultés si l’on observe qu’une lentille à bords minces agit sur un rayon lumineux comme le ferait un petit angle ayant sa base du côté de l’axe. Elle rabat donc vers l’axe tout rayon incident parallèle à cet axe.

Inversement tout rayon incident parallèle à l’axe d’une lentille à bords épais émerge en s’écartant de l’axe, la lentille agissant sur ce rayon comme le ferait un prisme de petit angle ayant son arête du côté de l’axe.

On peut d’ailleurs faire la théorie complète des lentilles minces en considérant une lentille mince comme équivalente à un prisme dont l’angle, nul sur l’axe, croît d’une façon continue, tout en restant très petit quand on s’écarte de l’axe.

Ceci explique d’ailleurs les représentations symboliques des deux types de lentilles.

6. Déviation d’un rayon lumineux. Unité de convergence

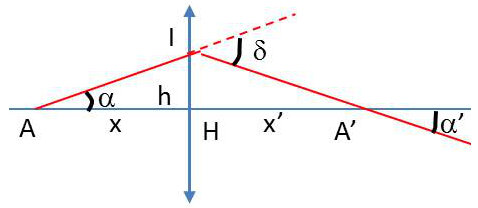Considérons un rayon provenant d’un point objet A sur l’axe, d’où il part en faisant un angle : \[\alpha=\frac{h}{AH}=-\frac{h}{x}\]

Le rayon émergent fait avec l’axe un angle : \[\alpha'=-\frac{h}{x'}\]

et la déviation imprimée au rayon est ainsi : \[\delta=\alpha'-\alpha=-h~\big\{\frac{1}{x'}-\frac{1}{x}\big\}=h~D\]

Ainsi \(\delta\) ne dépend pas du couple de points conjugués A et A’ choisis. Un rayon incident sur un point d’une lentille mince à la distance h de l’axe subit une déviation \(\delta\) indépendante de l’orientation du rayon (ceci n’a rien d’étonnant puisqu’on a vu qu’en un point déterminé une lentille est assimilable à un prisme de petit angle dont la déviation est pratiquement indépendante de l’incidence pourvu que celle-ci reste faible.

Le paramètre D caractérise donc l’aptitude d’une lentille à faire converger (ou diverger) les rayons.

La déviation imprimée à chaque rayon est d’autant plus grande que est plus grand ; il est donc logique d’appeler convergence de la lentille le paramètre D.

L’unité de convergence est celle d’une lentille qui a l’unité de longueur pour distance focale. Si on emploie le mètre comme unité de longueur, l’unité de convergence prend le nom de dioptrie.

7. Propriétés des foyers et du centre optique. Applications

7.1. Construire l’image d’un point B situé en dehors de l’axe principal

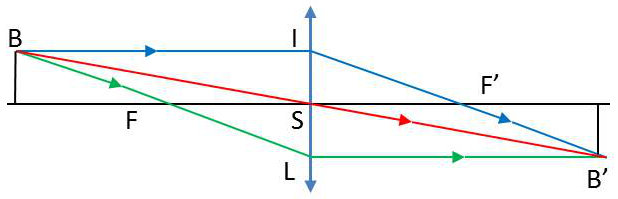On construit les rayons émergents correspondant à deux rayons incidents issus de B et on prend leur point d’intersection B’.

On choisit deux quelconques des trois incidents suivants :

• celui qui passe par le centre optique S qui continue sa route sans changer de direction ;

• celui qui passe par le foyer objet F ; il émerge parallèlement à l’axe principal ;

• celui qui est parallèle à l’axe ; il sort en passant par le foyer image F’

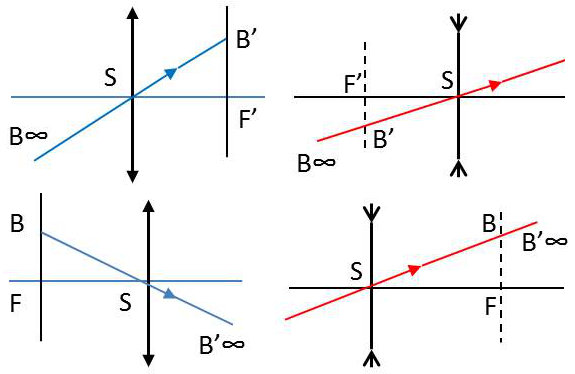Cas particuliers

1) Si B est à l’infini, B’ est dans le plan focal image et un seul rayon incident suffit pour le déterminer.

L’incident BS (axe secondaire passant par B) traverse la lentille sans déviation et perce le plan focal image au point cherché B’.

2) Si B est dans le plan focal objet, son image est à l’infini sur le rayon BS qui n’est pas dévié par son passage à travers la lentille.

7.2. Construire le rayon émergent qui correspond à un incident donné

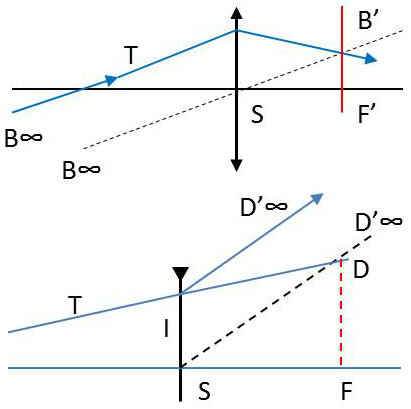Soit TI un incident quelconque, son émergent passe par I ; il suffit d’en connaître un deuxième point ou d’avoir sa direction.

Soit B le point situé à l’infini sur TI ; il a pour image le point B’ du plan focal image que l’on détermine en menant l’axe secondaire BSB’. Le rayon émergent qui doit passer par B’ est IB’.

Soit D le point où le rayon TI perce le plan focal objet.

Le point D a son image D’ à l’infini sur DS ; le rayon émergent cherché devant passer par D’ est la parallèle menée de I à l’axe secondaire DS.

7.3. Construire l’image d’un objet plan perpendiculaire à l’axe principal

Comme il a été dit, on construit l’image B’ de l’extrémité B de l’objet et on abaisse de B’ la perpendiculaire sur l’axe.

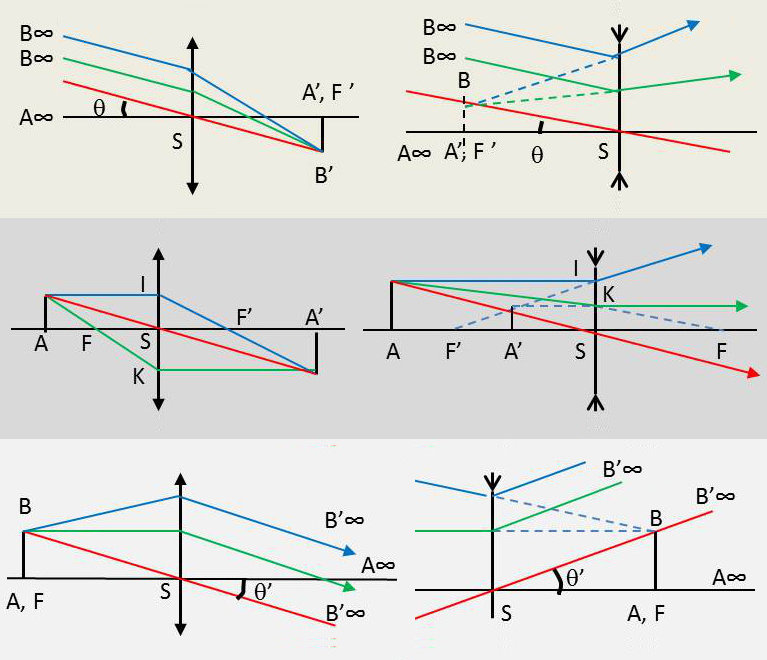a) Objet à l’infini

• Diamètre apparent \(\theta\).

• Construction de l’image A’B’ dans le plan focal image : \( A'B'=f'\theta \).

• Image renversée, réelle si la lentille convergente.

• Image droite, virtuelle si la lentille est divergente.

b) Objet dans le plan focal objet

L’image est à l’infini et son diamètre apparent est : \( \theta'=\cfrac{AB}{f}=-\cfrac{AB}{f'} \)

c) Position de l’objet quelconque

Construction de l’image d’un objet réel pour une lentille convergente et pour une lentille divergente.

8. Formules des lentilles minces. Discussion

Lentille convergente

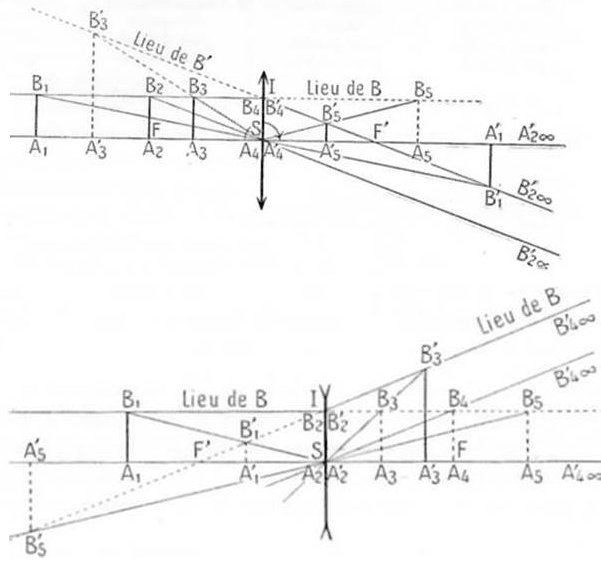D > 0 : En dédoublant l’axe optique, on montre comment l’image se déplace sur l’axe quand le pied de l’objet avance sur cet axe depuis l’infini réel jusqu’à l’infini virtuel.

Sur la figure, on voit comment varie en position, grandeur et orientation l’image d’un objet AB de grandeur constante que l’on fait glisser sur l’axe.

Lentille divergente

D < 0 : La lentille donne toujours une image virtuelle d’un objet réel.

Pour que l’image soit réelle, il faut et il suffit que l’objet soit virtuel et placé entre la lentille et son foyer objet.

9. Associations de lentilles minces

Un système centré peut être constitué par plusieurs lentilles minces dont les axes principaux sont confondus. Nous supposerons que les lentilles sont dans l’air.

9.1. Ensemble de deux lentilles minces accolées

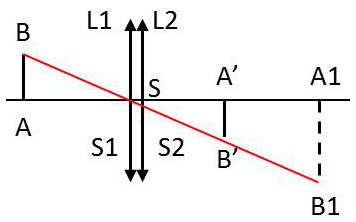La lentille \(L_1\) (centre optique en \(S_1\) et convergence \(D_1\)) est en contact avec la lentille \(L_2\) (centre optique \(S_2\) et convergence \(D_2\)).

La formule de Gullstrand donne (avec \(e=0\)) : \[D=D_1+D_2\] Il est évident d’autre part que les points principaux, H et H’, sont confondus sur les lentilles.

L’ensemble est donc équivalent à une lentille mince unique dont la convergence D est la somme des convergences des composantes.

La proposition peut être vérifiée immédiatement : \[L_1~:\quad\frac{1}{x'}-\frac{1}{x}=D_1 \quad;\quad L_2~:\quad\frac{1}{x'}-\frac{1}{x'_1}=D_2\]

D’où la relation de conjugaison : \[\frac{1}{x'}-\frac{1}{x}=D_1+D_2\]

Remarques

Si les lentilles sont de natures différentes et si leurs distances focales sont égales en valeur absolue : \[f'_1=-f'_2 \quad~; \quad \frac{1}{f'}=0\]

le système est afocal. Il se comporte comme une lame à faces parallèles mince.

Inversement, si en accolant une lentille convergente mince à une lentille divergente mince, on constate que l’ensemble est équivalent à une lame à faces parallèles, on peut affirmer que les distances focales des deux lentilles sont opposées ; si la distance focale de la lentille convergente est connue, on en déduit celle de la lentille divergente.

9.2. Ensemble de deux lentilles minces séparées. Doublet

Le système est défini si l’on connaît la distance \(e=S_1S_2\) des deux lentilles et leurs distances focales respectives \(f'_1,~f'_2\) . Un tel système porte le nom de doublet.

Les distances focales \(f'_1,~f'_2\) et l’intervalle e admettent souvent (au moins approximativement) un sous multiple commun a.

Ainsi on pourra poser : \[f'_1=m~a\quad~; \quad e=n~a\quad~; \quad f'_2=p~a\]

Il s’agit de nombres algébriques tels que m et p positifs ou négatifs, n toujours positif.

L’ensemble des trois nombres m, n, p se succédant dans l’ordre indiqué est ce que l’on appelle le symbole du doublet. Tous les doublets ayant même symbole seront homothétiques et leurs éléments cardinaux se correspondent dans cette homothétie.

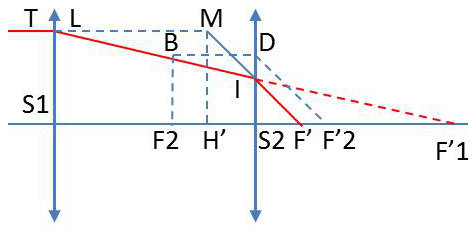Pour l’étude d’un doublet et la recherche de ses éléments cardinaux, nous appliquerons les résultats généraux établis dans les paragraphes précédents à ce cas particulier.

On fera pour cela : \(n=N=n'=1\).

La figure ci-contre nous montre la marche d’un rayon incident parallèle à l’axe et la détermination géométrique de la position du plan principal image.

Il est important de connaître surtout la position des foyers. Nous déterminons par exemple la position de F’ :

9.3. Position du foyer image F’

On applique les relations de Gullstrand :

\[\begin{aligned} D&=\frac{1}{f'_1}+\frac{1}{f'_2}-\frac{e}{f'_1~f'_2}=\frac{f'_1+f'_2-e}{f'_1~f'_2}\\ f'&=-f=\frac{1}{D}=\frac{f'_1~f'_2}{f'_1+f'_2-e}\end{aligned}\]

Remarques

Les plans principaux sont maintenant connus puisqu’on connaît la position des foyers et la convergence.

On peut aussi déterminer les points principaux H et H’ en tant que points nodaux en suivant la méthode du centre optique déjà utilisée pour les lentilles épaisses.

Soit en effet O un point de l’axe qui divise le segment \(S_1S_2\) dans le rapport (\(-\cfrac{f'_1}{f'_2}\)).

Si les hauteurs d’incidence sur les lentilles sont \(h_1=\overline{S_1I_1}\) et \(h_2=\overline{S_2I_2}\), on aura : \[\frac{h_2}{h_1}=\frac{\overline{OS_2}}{\overline{OS_1}}=-\frac{f'_2}{f'_1}\]

Les déviations \(\delta 1,~\delta 2\) en \(I_1,~I_2\) sont respectivement : \[\delta 1=-\frac{h_1}{f'_1}\quad~; \quad \delta 2=-\frac{h_2}{f'_2}\]

Et l’on a dans ces conditions : \[\delta2-\delta 1=0 \quad \text{ou} \quad \delta 1+\delta 2=0\]

On en conclut que le rayon émergent est parallèle à l’incident. En définitive, les points principaux H, H’ (ou N, N’) seront les conjugués de \(L_1\) ou \(L_2\) du centre optique O dont l’abscisse par rapport à \(S_1\) et \(S_2\) sera : \[\overline{S_1O}=e~\frac{f'_1}{f'_1+f'_2}\]

Dans le cas particulier où \(f'_1=f'_2\) (doublet symétrique), O est au milieu de \(S_1S_2\). Les éléments cardinaux sont symétriques par rapport à O.

10. Doublet afocal

La condition nécessaire et suffisante pour qu’un doublet soit afocal est que le foyer image de la première lentille \(S_1\) coïncide avec le foyer objet de la seconde \(S_2\) : \[\delta=0\quad~; \quad e~=~f'1+f'2\]

Si les deux lentilles sont convergentes, leurs distances focales respectives peuvent être quelconques. Si les lentilles sont l’une convergente et l’autre divergente, elles ne peuvent former un système afocal que si la distance focale de la lentille convergente est supérieure à la valeur absolue de la distance focale de la lentille divergente.

Deux lentilles divergentes ne peuvent jamais constituer un système afocal. Étudions le système afocal formé par deux lentilles convergentes \(S_1\) et \(S_2\) de distances focales respectives.

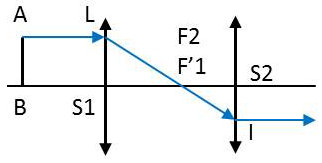Elles sont disposées comme indiqué sur la figure ci-contre, les points \(F'_1\) et \(F’_2\) étant confondus. Nous allons retrouver les résultats généraux établis dans un paragraphe précédent :

1) Soit AB un objet. Le rayon BL parallèle à l’axe rencontre en L la lentille \(S_1\). Il sort de cette lentille en passant par son foyer image, suivant \(LF'_1\) et perce en I la lentille \(S_2\).

Comme il passe par le foyer objet de cette dernière, il émerge du système parallèlement à l’axe, suivant Ix.

Si l’objet AB se déplace, le point B glisse sur BL et le point B’ décrit Ix ; l’image A’B’ conserve une grandeur constante. Par suite, le grandissement linéaire du système afocal est constant. Nous avons : \[\gamma_y=\frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{S_2I}}{\overline{S_2L}}=\frac{\overline{F_2S_1}}{\overline{SF'_1}}=-\frac{f'_2}{f'_1}\]

On pourra donc constituer un système afocal de grandissement \(\gamma_y\) fixé à volonté en associant deux lentilles simples dont les distances focales sont dans un rapport voulu (on pourra en particulier constituer une lunette astronomique).

2) Montrons directement que le grandissement angulaire du système est constant.

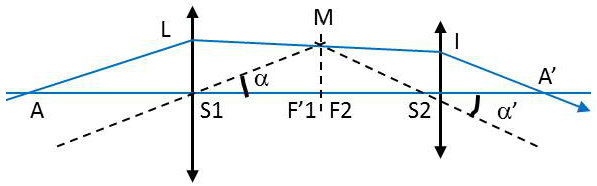Le rayon AL se réfracte une première fois suivant LMI, puis une seconde fois suivant IA’.

AL fait avec l’axe u angle \(\alpha\). IA’ fait avec l’axe l’angle \(\alpha'\).

Le grandissement angulaire pour le couple de points conjugués A et A’ est : \[\gamma_{\alpha}=\frac{\alpha'}{\alpha}\]

Nous retrouvons l’angle \(\alpha\) dans le triangle \(MS'_1F'_1\) qui nous donne : \[\alpha=\frac{F'_1M}{f'_1}\]

De même, le triangle \(MF_2S_2\) dans lequel l’angle en \(S_2\) n’est autre que l’angle \(\alpha'\) nous donne : \[\alpha'=-\frac{F'_2M}{f'_2}\]

Par suite : \[\gamma_{\alpha}=-\frac{f'_1}{f'_2}\]

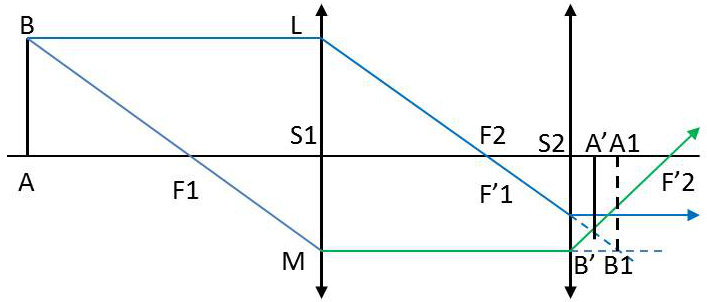3) Pour construire l’image A’B’, nous prendrons comme second rayon incident issu de B le rayon \(BF_1\) qui, entre les deux lentilles, chemine parallèlement à l’axe et sort en passant par \(F'_2\).

4) Nous pouvons préciser l’équation de conjugaison en prenant le foyer objet \(F_1\) de la première lentille pour origine des vecteurs relatifs à l’espace objet et en repérant la position du plan image par rapport au foyer image \(F'_2\) de la seconde lentille.

La relation de Newton appliquée successivement à chaque lentille donne :

\[\begin{aligned} \overline{F_1A}~~\overline{F'_1A_1}&=-{f'_1}^2 \\ \overline{F_2A_1}~~\overline{F'_2A'}&=-{f'_2}^2 \end{aligned}\]

Divisant membre à membre ces deux relations, il vient :

\[\frac{\overline{F'_2A'}}{\overline{F_1A}}=\big\{\frac{f'_2}{f'_1}\big\}^2\]

Nous retrouvons la forme générale de l’équation de conjugaison : \(F'1\) et \(F'2\) sont en effet deux points conjugués du système afocal. De plus, le rapport précédent n’est autre que le grandissement axial du système. Il est constant et égal au carré du grandissement linéaire.