1. Ouverture rectangulaire
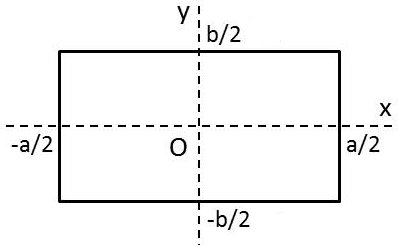On considère une pupille de dimensions [a,b]. On suppose que : \[t(x,y)= \left\{ \begin{aligned} &1\qquad \text{intérieur}\\ &0\qquad \text{extérieur} \end{aligned} \right.\]
D’où l’expression intégrale double portant sur le domaine rectangulaire : \[A=K~A_0\int\limits_{-a/2}^{+a/2}\exp\{j~\frac{2\pi~(\alpha'-\alpha)}{\lambda}~x\}~dx\int\limits_{-a/2}^{+a/2}\exp\{j~\frac{2\pi~(\beta'-\beta)}{\lambda}~y\}~dy\]
Or on sait que : \[\int_{-u}^{+u}\exp(j~\lambda x)~dx=2\alpha~\frac{\sin(\lambda u)}{\lambda u}=2\alpha~\operatorname{sinc}(\lambda u)\]
en utilisant pour simplifier la notation du sinus cardinal défini ainsi : \(\quad\operatorname{sinc}(x)=\cfrac{\sin(x)}{x}\)
On obtiendra donc tous calculs faits : \[A=K~A_0~a~b~\operatorname{sinc}(u)~\operatorname{sinc}(v)\qquad\text{avec :}~~ u=\frac{\pi a}{\lambda}~(\alpha'-\alpha)~~;~~v=\frac{\pi b}{\lambda}~(\beta'-\beta)\]
Le produit \((K~A_0~a~b)\) est l’amplitude diffractée dans la direction de l’onde incidente.
Si a et b sont tous deux grands, il n’y a pas d’amplitude diffractée en dehors de cette direction. En effet, pour que les fractions gardent une valeur finie (c’est-à-dire 1), il faut que \(\alpha'=\alpha\) et que \(\beta'=\beta\).
Avant d’aborder les figures de diffraction et les questions d’intensité, il sera plus facile de commencer à étudier ces problèmes avec une fente.
2. Cas d’une fente
On fait tendre un des côtés vers zéro, \(a\) par exemple, et pour simplifier le problème, nous supposerons une incidence normale à la fente c’est-à-dire \(\alpha=\beta=0\).
On a alors : \[A=K~A_0~a~b~\operatorname{sinc}\big(\frac{\pi a\alpha'}{\lambda}\big)~\operatorname{sinc}\big(\frac{\pi b\beta'}{\lambda}\big)\]
b étant très grand, la deuxième fraction devrait tendre vers zéro. On prendra donc \(\beta'=0\) et de la sorte cette fraction continuera d’exister avec la valeur limite « 1 ». D’où l’amplitude : \[A=K~A_0~a~b~\operatorname{sinc}\big(\frac{\pi a\alpha'}{\lambda}\big)\]
Et pour l’intensité : \[I=A~A^*=I_0~\operatorname{sinc}^2(u)\qquad\text{avec :}\quad u=\frac{\pi a\alpha'}{\lambda}\]
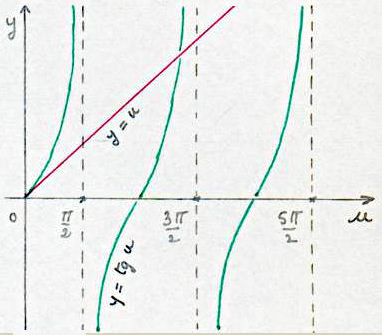Celle-ci est maximale pour le maximum de \(y=\cfrac{\sin(u)}{u}\), donc lorsque : \[y'=\frac{u\cos u-\sin u}{u^2}=0\]
Il faut alors résoudre l’équation \(u=\tan(u)\), ce qui ne peut être fait que graphiquement.
Ses racines, intersections de la droite et de la tangente, sont voisines de : \[\frac{3\pi}{2},~\frac{5\pi}{2},~\dots,~(2k+1)~\frac{\pi}{2}\]
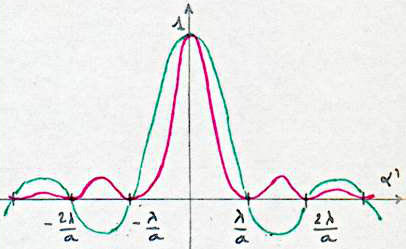On pourra représenter sur un même graphique les courbes d’amplitude et d’intensité en fonction de \(\alpha'\).
– En rouge : \(I/I_0\)
– En vert : \(A/K~A_0\)
Avec les valeurs significatives de \(u\) (donc de \(\alpha'\)) : \[u=\{0,~\pi,~3\pi/2,~5\pi/2,~3\pi\dots \}\]
Le dispositif expérimental est représenté ci-dessous :
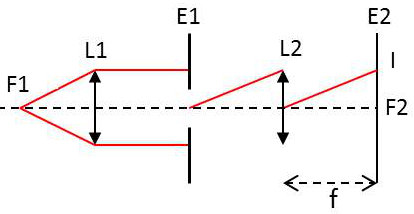\(S\) est une source ponctuelle et l’observation se fait sur un écran \(E_2\) dans le plan focal de la lentille \(L_2\), au voisinage d’un point \(I\).
On observe des franges plus ou moins lumineuses (interpolation de la courbe ci-dessus) et parallèles à la fente.
On peut les repérer dans un système d’axes \(F_2XY\) parallèle à celui de la fente et comme les angles sont petits, on a : \( X=\alpha'f~;~Y=\beta'f \)
Dans le cas de la fente (seule variable \(x\)) : \(X=\alpha'f\).
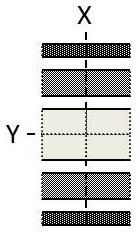La courbe montre qu’il y a un maximum d’intensité pour \(\alpha'= 0\). On dit que c’est un maximum principal.
Dans le plan d’observation, on est en \(X = 0\). La bande éclairée a pour largeur \(\Delta =2\lambda f/a\).
L’éclairement s’atténue du reste vers \(X=\pm\lambda/a\) où il est nul comme le montre la courbe.
Pour \(\alpha=\pm 3\lambda/2a\), l’intensité redevient maximale mais bien inférieure au maximum principal ; on dit que l’on a un maximum secondaire.
La largeur de bande a diminué de moitié. On en arrive finalement à l’extinction complète. On notera que les franges sont parallèles à la fente.
Remarques :
Si la source ponctuelle était remplacée par une source linéaire parallèle à la fente (filament, fente), cela ferait une infinité de sources ponctuelles. Pour chacune d’entre elles, on observe le phénomène précédent ; les franges subissent une translation parallèle au déplacement des sources et de sens contraire. On obtient ainsi tout un réseau de franges parallèles à la fente source.
Si la source linéaire et la fente sont croisées, le réseau de franges s’incline parallèlement à la source et si la source et la fente sont perpendiculaires, les franges disparaissent complètement.
3. Retour à l’ouverture rectangulaire
Nous allons supposer que la source est ponctuelle, que l’incidence est normale \((\alpha=\beta=0)\) et que les dimensions \([a,b]\) sont finies : \[I(\alpha',\beta')=I_0~\operatorname{sinc}^2\Big(\frac{\pi a\alpha'}{\lambda}\Big)~ \operatorname{sinc}^2\Big(\frac{\pi b\beta'}{\lambda}\Big)\]
C’est-à-dire : \[\frac{I(\alpha',\beta')}{I_0}=I(\alpha',0)~I(0,\beta')\]
On voit que \(I(\alpha',\beta')\) est le produit de deux termes dont chacun ne dépend seulement que de l’une des deux variables \(\alpha'\) ou \(\beta'\).
Le dispositif d’observation est le même que celui de la fente et, dans le plan focal de \(L_2\), on aura également \(X=\alpha'f\) et \(Y=\beta'f\).
Dans le plan focal, on observe deux séries de franges noires formant une sorte de quadrillage. Celles qui sont parallèles à \(oy\) correspondent à \(I(\alpha',0)\). Celles qui sont parallèles à \(ox\) correspondent à \(I(0,\beta')\) .
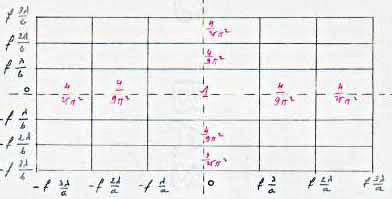Qu’observe-t-on dans ce plan focal ?
Des bandes noires parallèles aux axes de coordonnées délimitant des rectangles plus ou moins éclairés (maximum principal au centre et maximums secondaires ailleurs).
La valeur des maximums d’intensité est inscrite en rouge au centre des rectangles.
4. Ouvertures circulaires
On se place exactement dans les mêmes conditions que précédemment mais avec cette fois une symétrie de révolution autour de \(oz\).
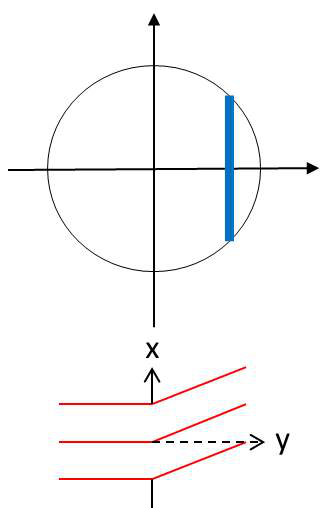On étudie la pupille suivant une coupe \(ox\) choisie de sorte que \(\beta' = 0\). L’amplitude devient alors : \[A=A_0\iint\limits_S\exp\Big\{j~\frac{2\pi\alpha'x}{\lambda}\Big\}~dx~dy\]
C’est-à dire : \[A=A_0\int_{-R}^{+R}\exp\Big\{j~\frac{2\pi\alpha'x}{\lambda}\Big\}~dx~\int_{-\sqrt{R^2-x^2}}^{+\sqrt{R^2-x^2}}dy\]
On a donc : \[A=4A_0\int_0^R\sqrt{R^2-x^2}~\exp\Big\{j~\frac{2\pi\alpha'x}{\lambda}\Big\}~dx\]
Le terme imaginaire de l’exponentielle fait partie de l’axe des \(y\) et, comme l’étude se fait dans le plan (\(Ox,Oz\)), il ne subsistera que la partie réelle : \[A=4A_0\int_0^R\sqrt{R^2-x^2}~\cos\frac{2\pi\alpha'x}{\lambda}~dx\]
Après le changement de variables \(x=R~t\) et \(\zeta=\cfrac{2\pi\alpha'R}{\lambda}\) : \[A=4~A_0~R^2\int_0^R\sqrt{1-t^2}~\cos(\zeta~t)~dt\]
À un facteur près, on reconnaît dans l’intégrale une fonction de Bessel d’ordre 1.
En effet : \[J_1(x)=\frac{2x}{\pi}\int_0^1\sqrt{1-t^2}~\cos(xt)~dt\]
Il s’ensuit que : \[A=2~A_0~R^2~\pi~\frac{J_1(\zeta)}{\zeta}\]
Les valeurs des zéros et des extrema des fonctions de Bessel sont connues au moyen de tables et on sait par ailleurs que si \(\zeta\rightarrow 0\), alors \(J_1(\zeta)\approx\zeta/2\).
Nous rappelons ici quelques éléments des tables correspondant à notre problème. \[\begin{matrix} &\zeta&0&3,832&5,126&7.015&8,417&10,173&11,620\\ &I/I_0={(2J_1/\zeta)}^2&1&0&0,0175&0&0,0041&0&0,0016 \end{matrix}\]
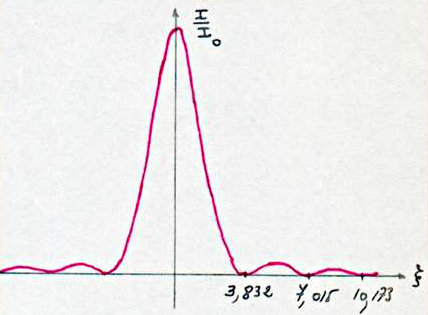Cette fois, à cause de la symétrie de révolution, nous n’aurons pas de franges, mais des anneaux brillants et sombres axés sur \(z’z\).
La courbe \(I / I_0\) montre que le centre est brillant et très intense.
Calculons le rayon de cet anneau lorsque l’observation se fait dans le plan focal d’une lentille :
\[\begin{aligned} &\zeta=\frac{2\pi R}{\lambda}~\alpha'=3,832\\ &\alpha'=\frac{\lambda}{2R}~\frac{3,832}{\pi}=\frac{1,22~\lambda}{2R}\end{aligned}\]
Le rayon de l’anneau a donc pour valeur : \[r=\alpha'f=\frac{1,22~\lambda}{2R}~f\]
