1. Définition
On appelle diffraction de Fresnel les phénomènes observés quand la source \(S\) et le plan \(P\) d’observation sont à distance finie et qu’il n’y a entre eux aucune conjugaison par un système optique. C’est à ces phénomènes que se rattache la formation des ombres.
2. Formule de Kirchoff
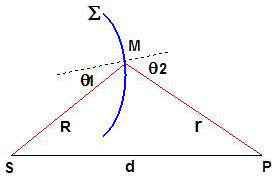La formule de Kirchoff traduit le principe de Huyghens dans les nouvelles conditions de l’expérience.
La vibration est envoyée de \(S\) en \(M\) puis de \(M\) en \(P\).
L’amplitude renvoyée par un élément \(ds\) autour de \(M\) sera : \[dA=f(\theta_1,\theta_2)\times\frac{A_0}{R}~\exp\big(-j~2\pi~\frac{R}{\lambda}\big)\times\frac{1}{r}\exp\big(-j~2\pi~\frac{r}{\lambda}\big)\]
\(A_0\) est l’amplitude en \(S\) ; \(f(\theta_1,\theta_2)\) est le facteur d’obliquité.
On démontre que : \[f(\theta_1,\theta_2)=\frac{j}{2}~\{\cos(\theta_1)+\cos(\theta_2)\}\]
Il suffit ensuite d’intégrer : \[A=A_0\iint\limits_{\Sigma}\frac{f(\theta_1,\theta_2)}{r~R}\exp\big(-j~2\pi~\frac{r+R}{\lambda}\big)~dS\]
3. Zones de Fresnel
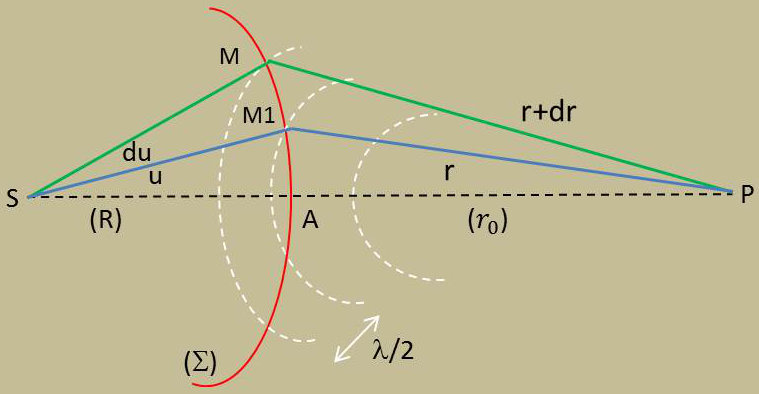\(S\) est le centre d’une onde sphérique \((\Sigma)\). Décomposons \((\Sigma)\) en zones élémentaires centrées sur \(SP\) et telles que :
\[\begin{aligned} PA&=r_0\\ PM_1&=r_0+\frac{\lambda}{2}\\ PM&=r_0+\frac{K\lambda}{2}\end{aligned}\]
Les vibrations envoyées par ces zones en \(P\) sont en opposition de phase consécutivement et en phase deux à deux.
Calculons les aires de ces zones réparties en révolutions autour de l’axe \(SP\) : \[d\sigma=(R~du)\times 2\pi\times\{R~\sin(u)\}=2\pi~R^2~\sin(u)~du\]
En introduisant la relation triangulaire (triangle \(MSP\)) : \[r^2=R^2+d^2-2~d~R~\cos(u)\]
Et en différentiant : \[r~dr=R~d~\sin(u)~du\]
Puis en éliminant \(\sin(u)~du\) et en considérant que les zones de Fresnel sont espacées de \(\lambda/2\) : \[d\sigma=\frac{2\pi R}{d}~r~dr=\frac{2\pi R}{d}~r\cdot\frac{\lambda}{2}\]
Ainsi, les zones de Fresnel ont-elles la même aire, à la variation de \(dr\) près. Cette variation est de fait très faible pour des zones voisines du pôle \(A\) de l’onde \((\Sigma)\).
Calcul des rayons des zones
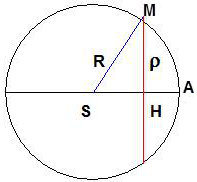Si on assimile chaque sphère limitant une zone à son plan tangent, on peut écrire, d’après les propriétés métriques du cercle : \[\rho_1^2=(2R-\lambda/2)~\frac{\lambda}{2}\approx\lambda~R\]
D’où, pour le rayon de la \(K^{\textit{ième}}\) zone : \[\rho_K^2=K~\lambda~R\qquad\Rightarrow\qquad\rho_K=\sqrt{K~\lambda~R}\]
Un calcul plus exact donnerait, en ayant posé \(SA=p\) et \(AP=p'\) : \[\rho_K=\sqrt{K\lambda}~\sqrt{\frac{p~p'}{p+p'}}\]
4. Éclairement par une ouverture circulaire
Si on place sur l’onde \(\Sigma\) un écran opaque percé d’une ouverture circulaire qui démasque la première zone de Fresnel, on trouve deux fois plus d’amplitude en \(P\), donc 4 fois plus d’intensité qu’avec l’onde entière.
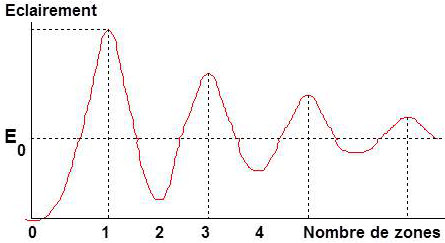
Précisons d’ailleurs que les dimensions des zones de Fresnel sur \(\Sigma\) dépendent de \(P\). Si on place une ouverture variable, on constate que l’éclairement passe par une série de maximums et de minimums.
Remarque
L’expérience peut être faite soit en prenant \(P\) fixe et en faisant varier l’ouverture, soit le contraire. Autour de \(P\), il se forme des anneaux et l’éclairement au centre de ces systèmes d’anneaux varie bien en fonction du nombre de zones de Fresnel comme l’indique la courbe calculée : le centre du système d’anneaux est brillant ou sombre selon que le nombre de zones est pair ou impair.
5. Éclairement par un petit écran circulaire
On suppose que l’écran est vu de \(P\) sous un angle assez petit pour que le facteur d’obliquité soir sensiblement égal à 1. On peut alors considérer les zones de Fresnel comme précédemment, à cette seule différence près que la première zone de Fresnel est un anneau dont le diamètre intérieur est égal au diamètre du petit écran.
En particulier, l’éclairement en \(P\) est égal au quart de l’éclairement qu’y enverrait seule la première zone annulaire. Mais le facteur d’obliquité de cette zone pouvant être confondu avec 1, cet éclairement est le même que si cette zone était remplacée par la zone polaire, c’est-à-dire le même que si l’écran n’existait pas.
On trouve donc encore un résultat d’apparence paradoxale, à savoir que l’éclairement en \(P\) est le même que si l’écran n’existait pas. Si l’écran devient plus grand ou si \(P\) s’en rapproche, le facteur d’obliquité diminue et l’éclairement devient plus faible.
En fait, on observe autour de \(P\) un système d’anneaux dont l’aspect varie suivant la dimension de l’écran, mais dont l’éclairement au centre est bien le même que si l’écran n’existait pas.
6. Réseaux zonés
Supposons que le facteur d’obliquité égal à 1. On sait alors que chaque zone de Fresnel tend à détruire l’action de sa voisine. Donc si l’on supprime une zone sur deux, l’éclairement de \(P\) peut être beaucoup plus grand qu’avec l’onde entière.
Il suffit d’imaginer un écran qui masque seulement les zones paires (ou impaires). Si on démasque \(N\) zones de Fresnel, l’amplitude de l’onde entière est multipliée par \(2N\), donc l’intensité par \(4N^2\).
Remarque
Un tel écran s’appelle un réseau zoné. Il s’obtient facilement en photographiant des anneaux dessinés et dont les intervalles sont alternativement blancs et noirs. Les rayons des anneaux et le coefficient de réduction de la photographie doivent être tels que, sur le réseau zoné, les rayons des anneaux soient : \[\rho_K=\sqrt{K\lambda}~\sqrt{\frac{p~p'}{p+p'}}\]
On peut alors écrire : \[\frac{1}{p}+\frac{1}{p'}=\frac{\lambda}{\rho_1^2}\]
On peut dire que ce réseau se comporte comme une lentille de distance focale : \[f=\frac{\rho_1^2}{\lambda}\]
Mais le réseau zoné réalise une concentration de lumière en \(P\) non seulement si sa zone centrale vaut une zone de Fresnel, mais aussi si elle en vaut un nombre impair.
On a alors : \[\rho_1=\sqrt{2K+1}~\sqrt{K}~\sqrt{\frac{p~p'}{p+p'}}\quad\Rightarrow\quad f_K=\frac{\rho_1^2}{(2K+1)~\lambda}\]
Il y a tout une série d’images de \(S\) correspondent aux différentes valeurs de \(f_K\).
Un réseau zoné est dit positif si sa zone centrale est transparente et négatif si elle est opaque.
7. Diffraction par un bord d’écran
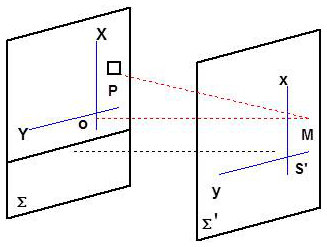Nous abordons le problème de la diffraction par un bord d’écran de manière succincte, car il est très délicat.
Calculons l’intensité diffractée en un point \(M\in\Sigma'\), d’abscisse \(x\), en prenant pour origine dans le plan d’intégration la projection \(O\) de \(M\).
La vibration élémentaire, diffractée par un élément de surface \(P\), d’aire \(dS=dX~dY\) et de coordonnées \((X,~Y)\) est de la forme : \[d\sigma=K~dX~dY\exp\{j(\omega t-\varphi)\}\]
\(\varphi\) est la différence de phase avec la vibration issue de l’origine \(O\) : \[\varphi=\frac{2\pi~\delta}{\lambda}=\frac{2\pi}{\lambda}~(PM-OM)\]
En combinant les relations géométriques :
\[\begin{aligned} OP^2&=MP^2-OM^2=(MP-OM)~(MP+OM)\\ OP^2&=X^2+Y^2\\ OM&\approx MP=f\end{aligned}\]
On obtient : \[\varphi\approx\frac{2\pi}{\lambda}~\frac{X^2+Y^2}{2f}\]
L’intégrale : \[s=\exp(j\omega t)\iint\limits_D\exp(-j\varphi)~dX~dY\]
pourra s’écrire : \[s=\exp(j\omega t)\int_{-x}^{+\infty}\exp\Big\{-j\frac{\pi X^2}{\lambda f}\Big\}~dX\int_{-\infty}^{+\infty}\exp\Big\{-j\frac{\pi Y^2}{\lambda f}\Big\}~dY\]
La deuxième intégrale ne dépend pas de la position du point \(M\) dans le plan ; c’est une constante.
En posant : \[\nu=\sqrt{\frac{2}{\lambda f}}~X\qquad;\qquad \nu_0=\sqrt{\frac{2}{\lambda f}}~x\]
l’amplitude complexe résultante en \(M\) s’écrit (à un facteur constant près) :
\[\begin{aligned} &A=\int_{-\nu_0}^{+\infty}\exp\Big(-j\frac{\pi~\nu^2}{2}\Big)~d\nu\\ &A=\int_{-\nu_0}^{+\infty}\cos\Big(\frac{\pi~\nu^2}{2}\Big)~d\nu-j\int_{-\nu_0}^{+\infty}\sin\Big(\frac{\pi~\nu^2}{2}\Big)~d\nu\end{aligned}\]
On reconnaît les intégrales de Fresnel : \[A=\{\zeta(+\infty)-\zeta(-\nu_0)\}-j\{\eta(+\infty)-\eta(-\nu_0)\}\]
C’est-à-dire : \[A=\big\{\frac{1}{2}+\zeta(\nu_0)\big\}-j\big\{\frac{1}{2}+\eta(\nu_0)\big\}\]
Valeur de l’interfrange
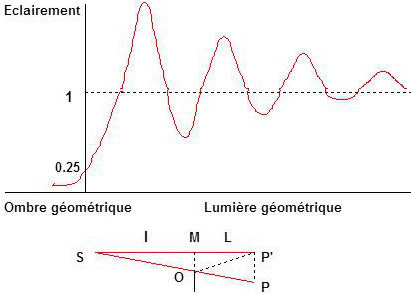Le premier maximum correspond à : \[(SOP')-(SMP')=\frac{\lambda}{2}\]
Des considérations géométriques montrent que :
\[\begin{aligned} &(OP')^2-(MP')^2=(OM)^2\\ &OP'-MP'=\frac{OM^2}{OP'+MP'}\end{aligned}\]
Or :
\[\begin{aligned} OP'&\approx L &MP'&\approx l &OP'-MP'&=\frac{OM^2}{2~L}\\ OS&\approx l &SM&\approx l &SO-SM&=\frac{OM^2}{2~l} \end{aligned}\]
On aura donc : \[(SOP')-(SMP')=OM^2\left(\frac{1}{2~L}-\frac{1}{2~l}\right)\]
D’où : \[OM=\sqrt{\frac{\lambda~l~L}{l+L}}\]
Mais on a également : \[\frac{PP'}{OM}=\frac{SP'}{SM}\]
Et en définitive : \[PP'=\sqrt{\frac{\lambda~(l+L)~L}{l}}\]
On observera un maximum pour \(\lambda\rightarrow(2K+1)~\lambda\) dans PP’.
On observera un minimum pour \(\lambda\rightarrow 2K\lambda\) dans PP’.
