1. Introduction
Dans le cas d’interférences à deux sources en lumière polychromatique, chaque longueur d’onde va donner son propre système de franges, les interfranges respectifs étant différents. On doit donc s’attendre à avoir des brouillages de franges présentant des aspects différents suivant la composition spectrale de la lumière émise par la source.
2. Cas de deux radiations monochromatiques
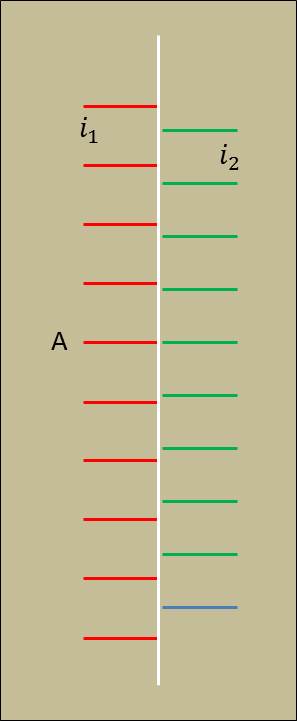 Supposons que l’on utilise le dispositif des fentes de Young.
Supposons que l’on utilise le dispositif des fentes de Young.
Nous aurons pour les interfranges les valeurs suivantes (cf. chapitres précédents) :
\[\begin{aligned} &\lambda_1~:\quad i_1=\frac{\lambda_1~D}{a}\\ &\lambda_2~:\quad i_2=\frac{\lambda_2~D}{a}\end{aligned}\]
-
a : distance entre les sources
-
D : distance des sources au plan d’observation
Aux points A, il y a concordance et on obtient des franges obscures parfaitement noires. Aux autres points, les franges sont en discordance. La distance \(AA'\) entre deux concordances est appelée la période du phénomène.
En supposant que \(i_2>i_1\), cette distance comprendra \(p\) interfranges \(i_1\) et \(p-1\) interfranges \(i_2\) de sorte que : \[p~i_1=(p-1)~i_2\qquad\Rightarrow\qquad p~\lambda_1=(p-1)~\lambda_2\]
On aura par suite : \[p=\frac{\lambda_2}{\lambda_2-\lambda_1}\]
Si les radiations sont très différentes (par exemple rouge et verte), il y aura au voisinage des coïncidences des franges brillantes de couleur mélangée rouge-vert et des franges bien noires.
Au voisinage des anti-coïncidences il n’y aura pas de franges noires mais seulement des franges alternativement rouges et vertes.
Si on utilise des couleurs voisines, produisant à peu près le même effet sur l’œil, par exemple deux raies jaunes, l’une de mercure et l’autre de sodium, il y aura au voisinage des anti-coïncidences un brouillage complet des franges remplacées par un éclairement uniforme.
Remarque
En un point, l’intensité produite est la somme des intensités dues aux diverses radiations : \[I=I_0\sin^2\frac{\pi\delta}{\lambda_1}+I_0\sin^2\frac{\pi\delta}{\lambda_2}\]
Mais on sait que : \[\delta=\frac{a~x}{D}~~\text{et}~~i=\frac{\lambda~D}{a}\qquad\Rightarrow\qquad\frac{\delta}{\lambda}=\frac{x}{L}\]
De sorte que : \[I=I_0\sin^2\frac{\pi x}{i_1}+I_0\sin^2\frac{\pi x}{i_2}\]
Posons \(i_1-i_2=\Delta\), alors : \[\frac{i_1-i_2}{i_2}=\frac{\Delta}{i_2}=\frac{i_1}{i_2}-1\]
Si on se place à la distance \(x~i_1\), on a :
\[\begin{aligned} &I=I_0\sin^2\pi x+I_0\sin^2\frac{\pi x~i_1}{i_2}\\ &I=I_0~\Big\{\sin^2\pi x+\sin^2\big(\pi x+\pi\frac{x\Delta}{i_2}\big)\Big\}\end{aligned}\]
Dans les conditions où \(\lambda_1\approx\lambda_2\), alors \(i_1\approx i_2\), donc \(\cfrac{\Delta}{i_2}\) est très petit. La quantité \(\cfrac{x\Delta}{i_2}\) varie beaucoup plus lentement que \(x\) et nous pouvons négliger ses variations dans une région contenant quelques franges.
Si, dans cette région, \(\cfrac{x\Delta}{i_2}=k\) entier, alors on a : \[I=2I_0\sin^2\pi x^2\]
Les franges sont exactement les mêmes qu’en lumière monochromatique.
Si au contraire \(\cfrac{x\Delta}{i_2}=k+\cfrac{1}{2}\) , on aura alors : \[I=I_0~\Big\{\sin^2\pi x+\sin^2\big(\pi x+k\pi+\frac{\pi}{2}\big)\Big\}\]
L’éclairement est uniforme, les franges ont disparu.
3. Phénomène en lumière blanche
Deux radiations de longueurs d’onde différentes ne peuvent interférer.
La lumière blanche étant constitué par un ensemble de longueurs d’onde différentes, en un point \(M\) quelconque, l’intensité sera la somme des intensités correspondant aux diverses longueurs d’onde composantes.
La frange centrale coïncidant pour toutes les couleurs, on observe au centre du phénomène une frange blanche \(O\), bordée de deux franges qui paraissent noires.
Mais dès la frange brillante suivante apparaissent des irisations. À mesure que l’on s’écarte de la frange centrale, les couleurs sont de plus en plus lavées de blanc et de moins en moins perceptibles.
En effet, soit un point où : \[\delta=6~\mu m=15\times 0,4~\mu m\approx 14\times 0,43~\mu m\approx 8\times 0,75\mu m\approx\dots\]
Entre les limites \([0,4\mu m~;~ 0,75\mu m]\), il y a, y compris ces limites, 8 radiations réparties dans tout le spectre dont l’intensité est maximale. Leur superposition donne à l’œil une impression de blanc. C’est ce que l’on appelle un blanc d’ordre supérieur.
En lumière monochromatique, nous observions une infinité de franges. Ici, on ne peut observer plus de 5 ou 6 franges de chaque côté de la frange centrale.
En un point éloigné du centre, on doit observer avec un spectroscope dont la fente est parallèle aux franges : on voit un spectre cannelé, c’est-à-dire dont les franges sont alternativement brillantes et sombres.
Par exemple, pour \([0,4\mu m~;~0,75\mu m]\), on a 7 cannelures brillantes séparées par 6 noires.
Spectres cannelés
Supposons que l’on fasse l’expérience avec les fentes de Young et que l’on observe l’écran en plaçant la fente du spectroscope à la distance \(x_0\) du centre.
Les radiations manquantes du spectre sont celles qui donnent sur la fente du spectroscope une frange noire satisfaisant à la relation : \[\delta=\frac{a~x_0}{D}=(2k+1)~\frac{\lambda}{2}\qquad\Rightarrow\qquad\lambda=\frac{2a~x_0}{(2k+1)~D}\]
Les valeurs (entières) de \(k\) sont celles pour lesquelles \([0,4\mu m~;~0,75\mu m]\). Connaissant \(k\), on trouve les diverses valeurs de \(\lambda\) en \(x_0\).

