1. Propriétés principales des corps cristallins

L’étude des propriétés physiques des cristaux (dureté, conductivité thermique, coefficient d’élasticité, etc.) montre que, en général, ces propriétés varient avec la direction considérée : ces cristaux sont dits anisotropes.

Les propriétés d’un cristal peuvent avoir une même valeur dans plusieurs directions et l’on décide suivant ces directions des symétries, de diverses natures et souvent complexes.

La plupart des cristaux se comportent de façon inattendue par rapport à la lumière : tout rayon de lumière est décomposé en deux rayons à polarisation plane qui ont des indices de réfraction différents. Autrement dit, ces rayons se propagent à des vitesses différentes dans le milieu cristallin.

On peut expliquer facilement les propriétés observées dans les cristaux si l’on admet que tout corps cristallisé a une structure réticulaire (en réseau) qui est indépendante de la nature et de la forme des particules élémentaires (atomes) constituant le cristal. C’est pour cette raison que, pour représenter schématiquement une structure cristalline, on emploie un réseau à trois dimensions.

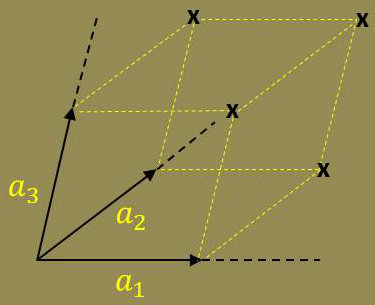Ce réseau peut être représenté par une infinité de parallélépipèdes élémentaires identiques disposés parallèlement les uns aux autres et remplissant entièrement l’espace sans laisser de vide :

• Les sommets de ces parallélépipèdes sont les nœuds du réseau.

• Les droites qui les joignent sont des rangées et les plans qui contiennent trois nœuds qui ne sont pas d’une même rangée sont les plans réticulaires.

• Ces parallélépipèdes sont les mailles du réseau.

En choisissant comme axes de coordonnées trois rangées du réseau et en prenant comme unité de longueur les segments séparant deux nœuds consécutifs sur chacune des rangées adaptées comme axes, la position d’un plan réticulaire quelconque s’exprime à l’aide de trois nombres entiers. C’est le problème classique de l’équation du plan en géométrie analytique 3D.

Corps cristallisés et corps amorphes

Un cristal est un corps solide à structure réticulaire. L’absence de structure réticulaire caractérise un corps amorphe. Pour ces corps amorphes, la température de fusion n’est pas très bien déterminée. Les corps amorphes sont par ailleurs isotropes. L’isotropie est l’indépendance de direction de variations des propriétés du corps.

2. Étude analytique du cristal

En 1855, Bravais a déterminé les réseaux tridimensionnels fondamentaux que l’on peut déduire par translation.

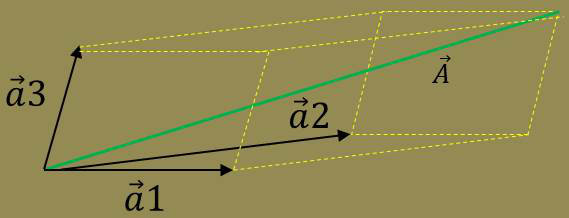
En prenant un atome origine et le trièdre de référence \([O,~\vec{a}_1,~\vec{a}_2,~\vec{a}_3]\) le cristal apparaît comme une infinité de parallélépipèdes construits sur ce parallélépipède élémentaire.

Autrement dit, le parallélépipède obtenu est construit à partir des translations : \[\overrightarrow{A}=p\overrightarrow{a}_1+q\overrightarrow{a}_2+r\overrightarrow{a}_3\]

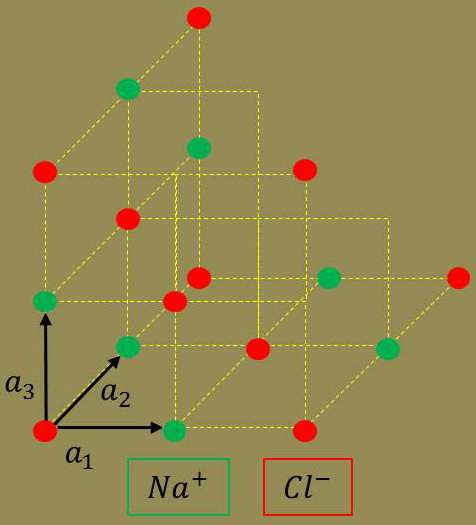Par exemple, le cristal de \(NaCl\) présente une triple périodicité, car on peut faire :

\[\begin{aligned} p=2\quad&;\quad q=r=0\\ p=r=0\quad&;\quad q=2\\ p=q=0\quad&;\quad r=2\end{aligned}\]

Le cristal reste invariant après l’une quelconque des translations A. On dit que le cristal infini est invariant avec une translation du réseau de Bravais.

Il existe d’autres opérations qui laissent le réseau invariant :

Une maille possède une symétrie d’ordre \(n\) pour un axe si au cours d’une rotation de \([2\pi/n]\) autour de cet axe, la maille se superpose à elle-même.

Par exemple :

• \(n=2\)symétrie habituelle

• \(n=3\)triangle équilatéral, axe perpendiculaire au plan et passant par G

• \(n=4\)cas de l’hexagone régulier

Remarque

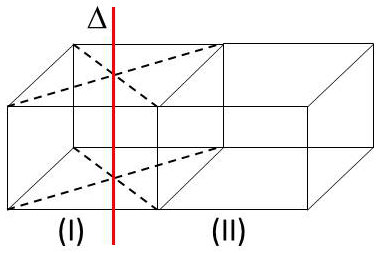
Un axe de symétrie pour une maille n’est axe de symétrie pour le cristal que si celui-ci est infini.

Prenons en effet un cristal cubique. \(\Delta\) est axe d’ordre 4 pour \([I]\), mais pas pour \([I]\cup[II]\).

Il faudrait un cube [I] de plusieurs cubes pour en faire un gros, d’axe \(\Delta\).

Plans réticulaires

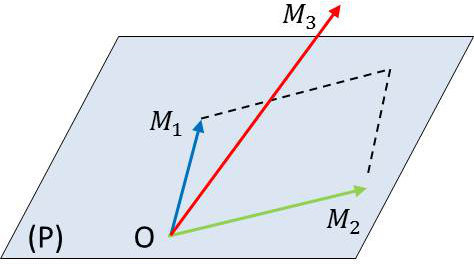Soient trois atomes de cristal placés en \(O\), \(M_1\) et \(M_2\) avec : \[\overrightarrow{M_1}=\overrightarrow{a_1}\quad;\quad \overrightarrow{M_2}=\overrightarrow{a_2}\qquad\lambda~,~\mu~\text{entiers}\]

Tous les points M tels que \(\overrightarrow{OM}=\lambda\overrightarrow{a}_1+\mu\overrightarrow{a}_2\) sont aussi des points du réseau. L’ensemble de ces points définit un plan réticulaire.

On considère un atome \(M_3\notin P\) le plus près possible de P tel que \(\overrightarrow{OM}=\overrightarrow{a}_3\).

Si à l’ensemble du réseau on fait subir la translation \(\overrightarrow{a_3}\), il reste invariant.

Dans la translation \(\overrightarrow{a_3}\), on a \(P\rightarrow P'\) : \(P'\) est encore un plan réticulaire.

Entre deux plans réticulaires successifs, il n’y a pas d’atomes. On peut considérer que les atomes du cristal sont répartis en plans réticulaires parallèles et équidistants.

3. Systèmes cristallins

Les systèmes cristallins sont définis à partir du parallélépipède élémentaire engendrant un trièdre de référence. Ce trièdre est caractérisé par les vecteurs unitaires \([\vec{a},~\vec{b},~\vec{c} ]\) et les angles \([\alpha,~\beta,~\gamma ]\) des faces du trièdre.

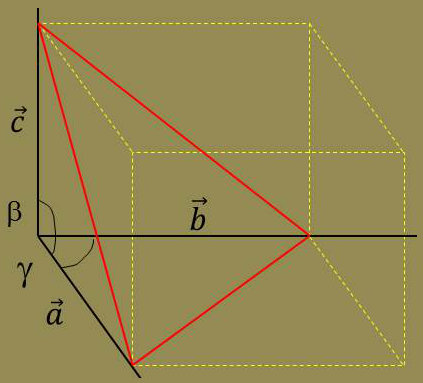On distingue sept systèmes :

\[\begin{aligned} &a=b=c &&\alpha=\beta=\gamma=90^o &&\text{cubique}\\ &a=b\neq c &&\alpha=\beta=\gamma=90^o &&\text{quadratique}\\ &a\neq b\neq c &&\alpha=\beta=\gamma=90^o &&\text{rhombique}\\ &a=b=c &&\alpha=\gamma=90^o~;~\beta\neq 90^o &&\text{monoclinique}\\ &a\neq b\neq c &&\alpha\neq\beta\neq\gamma=90^o &&\text{triclinique}\\ &a=b\neq c &&\alpha=\beta=\gamma\neq 90^o &&\text{trigonal}\\ &a=b=c &&\alpha=\beta=90^o~;~\gamma=120^o &&\text{hexagonal}\end{aligned}\]

4. Indices de Miller

On peut définir le cristal à partir des plans réticulaires. Il suffit de choisir un vecteur \(\overrightarrow{B}\) définissant la direction de ces plans et l’équidistance \(d\) de ces plans. \(\overrightarrow{B}\) est normal à ces plans et on a : \[|\overrightarrow{B}|=\frac{2\pi}{d}~n\]

On décompose ce vecteur en vecteurs non coplanaires : \[\overrightarrow{B}=h\overrightarrow{b}_1+k\overrightarrow{b}_2+l\overrightarrow{b}_3\qquad\text{h,k,l~~indices de Miller}\]

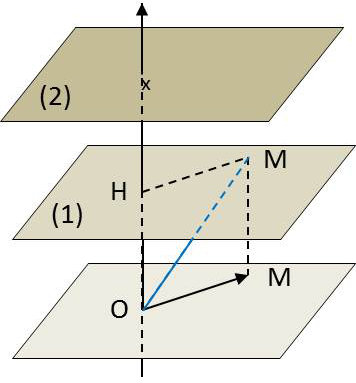Si \(O\) et\(M\) sont dans un même plan réticulaire : \[\overrightarrow{B}\centerdot\overrightarrow{A}=0\qquad\text{avec}\qquad \overrightarrow{OM}=\overrightarrow{A}=p~\overrightarrow{a_1}+q~\overrightarrow{a_2}+r~\overrightarrow{a_3}\]

L’expression du produit scalaire est simplifiée en posant : \[\overrightarrow{b_i}\centerdot\overrightarrow{a_j}=2\pi~\delta_{ij}\]

Si \(M\) appartient au premier plan réticulaire après \(O\), on a : \[\overrightarrow{B}\centerdot\overrightarrow{A}=\overline{OH}~|\overrightarrow{B}|=\frac{2\pi}{d}~d=2\pi\]

Pour le N-ième plan réticulaire : \[\overrightarrow{B}\centerdot\overrightarrow{A}=\frac{2\pi}{d}~nd=2n\pi\]

Par suite : \[hp+kq+lr=n\qquad\forall B\qquad p,~q,~r~\text{entiers}\quad\Rightarrow\quad h,k,l~ \text{entiers}\]

Remarque

Soit \(M\) un point du plan réticulaire le plus proche de l’origine :

\[\begin{aligned} \overrightarrow{OM}&=x\overrightarrow{a}_1+y\overrightarrow{a}_2+z\overrightarrow{a}_3\\ \overrightarrow{B}&=h\overrightarrow{b}_1+k\overrightarrow{b}_2+l\overrightarrow{b}_3\\ \overrightarrow{B}\centerdot\overrightarrow{OM}&=2\pi=2\pi(hx+ky+lz)\ \Rightarrow \ \ hx+ky+lz=0\end{aligned}\]

On reconnaît l’équation d’un plan qui passe par les extrémités de \([\vec{a}_1,~\vec{a}_2,~\vec{a}_3]\) à ce que \(h = k = l = 1\).

Cas particuliers

Dispositions particulières des indices pour les plans parallèles à un axe donné :

\[\begin{aligned} &(P)~//~\vec{a}\qquad\{0,~k,~l\}\\ &(P)~//~\vec{b}\qquad\{h,~0,~l\}\\ &(P)~//~\vec{c}\qquad\{h,~k,~0\}\end{aligned}\]

Technique de calcul pour un plan réticulaire quelconque

On sait que les indices de Miller sont des nombres entiers proportionnels aux inverses des longueurs interceptées par chacun des trois axes.

Nous ferons ce calcul simple avec un exemple (figure ci-contre).

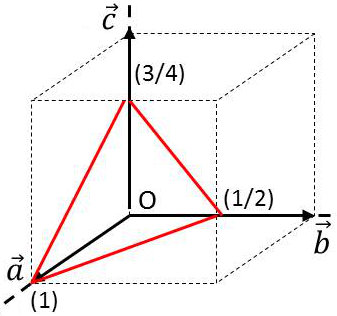- Première étape :

\[\begin{aligned} \overrightarrow{OA}=\vec{a} \quad&\Rightarrow \quad h=1\\ \overrightarrow{OB}=\frac{1}{2}~\vec{b} \quad&\Rightarrow \quad k=2\\ \overrightarrow{OC}=\frac{3}{4}~\vec{c} \quad&\Rightarrow \quad l=\frac{4}{3}\end{aligned}\]

- Deuxième étape (normalisation) :

En multipliant par 3 tous les indices, il vient : \[h=3~~;~~k=6~~;~~l=4\]

Ce sont les valeurs cherchées.