1. Une optique des rayons X ?
Comme pour la lumière visible, la longueur d’onde des rayons \(X\) varie, entre 0,1 et 10 Å.
Les rayons de faible longueur d’onde sont dits rayons durs (très pénétrants) ; les autres sont les rayons mous (peu pénétrants).
La courbe de l’indice de réfraction \(n(\lambda)\) obtenue dans l’étude des ondes électromagnétiques montre que pour des valeurs aussi faibles de \(\lambda\), on a \(n < 1\).
De ce fait, le rayon X ne peut être étudié comme le serait un rayon lumineux classique se propageant dans le vide ou dans un milieu donné.
2. Réflexion
Du fait que \(n < 1\), il résulte qu’un faisceau de rayons X tombant sur la surface de la substance sous une incidence presque rasante entraîne qu’il peut subir une réflexion totale.
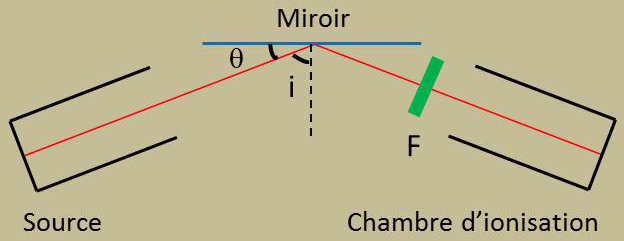 L’angle limite \(\theta_m\) a été mesuré par Compton suivant le dispositif représenté ci-contre. La condition de réflexion totale est : \[\sin(i)\geq n\qquad\text{ou}\qquad\cos(\theta)\geq n\]
L’angle limite \(\theta_m\) a été mesuré par Compton suivant le dispositif représenté ci-contre. La condition de réflexion totale est : \[\sin(i)\geq n\qquad\text{ou}\qquad\cos(\theta)\geq n\]
Et l’angle \(\theta\) étant très petit : \[\cos(\theta)\approx 1-\theta^2/2\geq n \qquad\Rightarrow\qquad \theta_m\leq\sqrt{2(1-n)}\]
Compton réussit à retrouver 80 à 90 % de l’énergie incidente à partir d’un certain angle \(\theta_m\). L’expérience a montré que \(\theta_m\) était proportionnelle à \(\lambda\).
Pour le quartz et pour la raie \(K_{\alpha}\) du cuivre (\(\lambda\) = 1,542 Å), des mesures très récentes ont donné \(\theta_m\) = 14’ 13". On obtient alors : \[n=\cos(\theta_m)\approx 1-\theta^2/2=1-8,56~10^{-6}\]
3. Réfraction
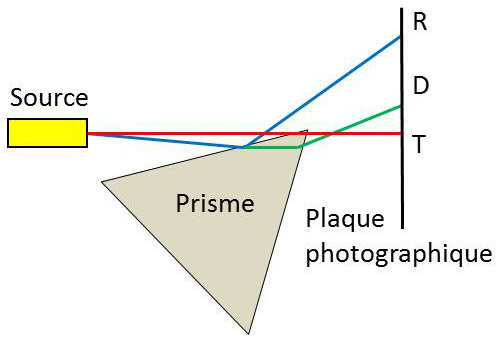 La déviation des rayons X par un prisme de verre a pu être observée par Siegbahn, en prenant la précaution d’employer un faisceau très fin dont le rayon moyen fait approximativement avec la face d’entrée du prisme d’angle limite \(\theta_m\).
La déviation des rayons X par un prisme de verre a pu être observée par Siegbahn, en prenant la précaution d’employer un faisceau très fin dont le rayon moyen fait approximativement avec la face d’entrée du prisme d’angle limite \(\theta_m\).
On observe sur la plaque photographique :
-
la trace T des rayons directs (passés au-dessus de l’arête) ;
-
la trace R des rayons réfléchis totalement ;
-
la tache D pour les rayons faisant un angle \(\theta>\theta_m\).
Cette déviation est contraire à celle connue de l’optique usuelle.
Si le faisceau contient plusieurs radiations, la tache D forme un véritable spectre de dispersion.
L’expérience montre donc aussi que \(n < 1\) et la mesure de la déviation des différentes raies montre bien que \((1-n)\) est proportionnelle à \(\lambda^2\).
4. Diffraction
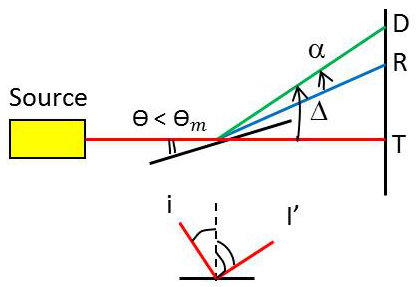 On opère sur un réseau plan en incidence rasante \(\theta<\theta_m\). Dans ce cas :
On opère sur un réseau plan en incidence rasante \(\theta<\theta_m\). Dans ce cas :
\[\begin{aligned} a~\{\sin(i)-\sin(i')\}&=k\lambda\\ \sin(i)-\sin(i')&=nk\lambda\quad;\quad n=1/a\end{aligned}\]
Or on a : \[i=\frac{\pi}{2}-\theta\quad;\quad i'=\frac{\pi}{2}-(\Delta-\theta)\]
Il vient : \[\cos(\theta)-\cos(\Delta-\theta)=nk\lambda\]
On observe en T une tache très sombre, de même qu’en R. En D, on observe un spectre de raies (moins sombres).
On exploite l’expérience en transformant la formule précédente : \[\cos(\theta)\approx (1-\theta^2)\quad;\quad\cos(\Delta-\theta)\approx 1-\frac{(\Delta-\theta)^2}{2}\]
D’où la formule définitive : \[\alpha=\Delta-2\theta\qquad\Rightarrow\qquad\frac{\alpha\Delta}{2}=nk\lambda\]
Cette expérience est extrêmement importante et permet d’obtenir \(\lambda\).
5. Réflexion par un réseau cristallin
La structure cristalline et l’existence des plans réticulaires sont supposées connues. Les atomes diffractent chacun une partie du faisceau de rayons X que le cristal reçoit. On est donc conduit à étudier un problème de réseau, supposé plan pour simplifier.
5.1. Conditions de Laue
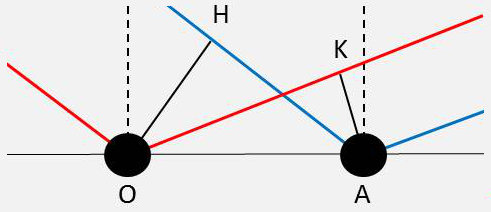 Soit O l’atome origine du réseau ; les autres atomes A du réseau en sont déduits par translation : \[\overrightarrow{OA}=\overrightarrow{a}=p~\overrightarrow{a_1}+q~\overrightarrow{a_2}+r~\overrightarrow{a_3}\qquad p,~q,~r ~ \text{entiers}\]
Soit O l’atome origine du réseau ; les autres atomes A du réseau en sont déduits par translation : \[\overrightarrow{OA}=\overrightarrow{a}=p~\overrightarrow{a_1}+q~\overrightarrow{a_2}+r~\overrightarrow{a_3}\qquad p,~q,~r ~ \text{entiers}\]
Calculons le déphasage entre le rayon diffracté par O et celui diffracté par A : \[\delta=HA-OK\qquad\Rightarrow\qquad\varphi=\frac{2\pi}{\lambda}~\delta=\frac{2\pi}{\lambda}~(HA-OK)\]
Partant de l’expression des vecteurs d’onde (voir la définition dans le cours d’optique physique) : \[\overrightarrow{k}=\frac{2\pi}{\lambda}~\vec{u} \quad;\quad \overrightarrow{k'}=\frac{2\pi}{\lambda}~\vec{u'}\]
on obtient : \[\varphi(\overrightarrow{k}-\overrightarrow{k'})\centerdot\overrightarrow{a}\]
Si l’amplitude en O est \(A_0\), celle en un atome quelconque sera : \[A=A_0~\exp(-j\varphi)=A_0~\exp\big\{j(\overrightarrow{k'}-\overrightarrow{k})\centerdot\overrightarrow{a}\big\}\]
Pour l’amplitude totale : \[A=\sum_{\vec{a}}A_0~\exp\big\{j(\overrightarrow{k'}-\overrightarrow{k})\centerdot\overrightarrow{a}\big\}\]
Les ondes en phase seront telles que \(\varphi=\mod 2\pi\) :
\[\begin{aligned} &\big(\overrightarrow{k'}-\overrightarrow{k}\big)\centerdot\overrightarrow{a_1}=2\pi~p\\ &\big(\overrightarrow{k'}-\overrightarrow{k}\big)\centerdot\overrightarrow{a_2}=2\pi~q\\ &\big(\overrightarrow{k'}-\overrightarrow{k}\big)\centerdot\overrightarrow{a_3}=2\pi~r\end{aligned}\]
En cristallographie, on introduit une base \(\overrightarrow{b}_i\) telle que : \[\overrightarrow{b_i}\centerdot\overrightarrow{a_j}=2\pi~\delta_{ij}\]
D’où les conditions de Laue : \[\overrightarrow{k'}-\overrightarrow{k}=p~\overrightarrow{b_1}+q~\overrightarrow{b_2}+r~\overrightarrow{b_3}\]
5.2. Conditions de Bragg
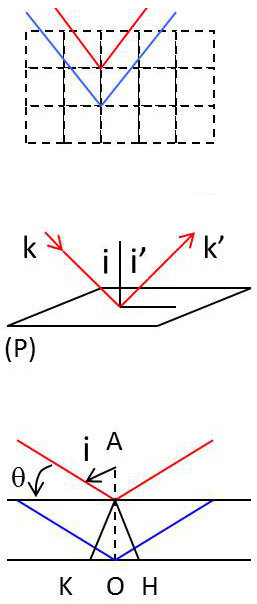 On a vu en cristallographie que le plan réticulaire passant par l’origine O était défini par : \[\big(\overrightarrow{k'}-\overrightarrow{k}\big)\centerdot\overrightarrow{a}=0\]
On a vu en cristallographie que le plan réticulaire passant par l’origine O était défini par : \[\big(\overrightarrow{k'}-\overrightarrow{k}\big)\centerdot\overrightarrow{a}=0\]
Cela signifie que les ondes diffractées par ce plan sont en phase et que : \[projection_{sur P}(\overrightarrow{k'})=projection_{sur P}(\overrightarrow{k})\quad\Rightarrow\quad i=i'\]
Pour le plan réticulaire le plus proche, on a : \[(\overrightarrow{k'}-\overrightarrow{k})\centerdot\overrightarrow{a}=2\pi\]
Pour le p-ième plan, le déphasage sera : \[(\overrightarrow{k'}-\overrightarrow{k})\centerdot\overrightarrow{a}=2\pi~p\]
On a donc : \[\delta=KO+OH=2~OK=2d\cos(i)=2d\sin(\theta)\]
D’où le déphasage : \[\varphi=\frac{4\pi}{\lambda}~d~\sin(\theta)\]
Remarque
Il y a équivalence entre les relations de Bragg et de Laue.
Du fait que \(i'=i\), le vecteur \((\vec{k'}-\vec{k})\) est porté par \(\vec{n}\) normale au plan P. Par ailleurs : \[|\vec{k}|=|\vec{k'}|=\frac{2\pi}{\lambda}\]
On a donc : \[|\vec{k}-\vec{k'}|=\frac{2\pi}{\lambda}~2\cos(i)=\frac{2\pi}{\lambda}~2\sin(\theta)=\frac{2\pi}{\lambda}~\frac{p\lambda}{d}=p~\frac{2\pi}{d}=|\vec{n}|\]
On retrouve la condition de Laue.
5.3. Vérification de la formule de Bragg
On peut imaginer facilement le dispositif utilisé par les frères Bragg. Le faisceau réfléchi était reçu dans une chambre d’ionisation reliée à un électromètre. En enregistrant la charge, on en déduisait l’intensité \(i\). En traçant la courbe \(\theta(i)\), les frères Bragg ont remarqué des maximums très nets pour certaines valeurs de \(\theta\) pour lesquelles la réflexion avait lieu. Ils ont ainsi vérifié que :
\[\frac{\sin(\theta_1)}{1}=\frac{\sin(\theta_2)}{2}=\frac{\sin(\theta_3)}{3}=\cdots=\frac{\lambda}{2d}\]
Les mesures faites avec les rayons K du palladium sur un cristal de sel gemme ont donné les résultats suivants : \[\theta=6^o,~12^o,~18^o\qquad\text{avec}\qquad\frac{\lambda}{2d}=0,1\]
Remarque
En fait, la formule de Bragg n’est pas très rigoureuse. Jusqu’à présent, on a négligé les vibrations émises par les électrons des atomes excités par le passage de l’onde incidente et qui se traduisent par \(n\neq 1\). Ces vibrations s’ajoutent à l’onde incidente.
Supposons la face d’entrée parallèle aux plans réticulaires. En toute rigueur, on doit écrire : \[\delta=2n~d\cos(r)=p~\lambda\]
Par suite : \[\sin(i)=\cos(\theta)=n\sin(r)\quad\Rightarrow\quad p~\lambda=2d~\sqrt{n^2-\cos^2(\theta)}\]
Mais on sait que \((1-n)\) est proportionnel à \(\lambda^2\), soit : \[1-n^2=k~\lambda^2\]
On trouve alors que : \[p~\lambda=2d~\sin(\theta)\sqrt{1-\frac{2k~\lambda^2}{\sin^2(\theta)}} \approx 2d~\sin(\theta)~\left\{1-\frac{k~\lambda^2}{\sin^2(\theta)}\right\}\]
Or, de façon approchée : \[p~\lambda=2d~\sin(\theta)\]
On a donc : \[p~\lambda=2d~\sin(\theta)~\left\{1-\frac{4k~d^2}{p^2}\right\}\]
On voit donc que l’erreur sur la formule de Bragg est d’autant plus petite que \(p\) est très grand.

