1. Considérations générales

Un oscillateur rigoureusement périodique garde dans le temps une amplitude constante. Pratiquement, les oscillations finissent par s’arrêter et l’oscillateur tend vers une certaine position d’équilibre : on dit que les oscillations sont amorties. En d’autres termes, si nous considérons un oscillateur soumis à une force ou un couple de rappel proportionnel à l’élongation, l’énergie de vibration n’est pas invariable dans le temps ; elle diminue avec le temps.

On est donc amené à admettre l’existence de forces et de couples qui accomplissent des travaux négatifs et qui contribuent à une diminution continue de l’énergie de l’oscillateur. Ces forces et couples dont les travaux sont constamment négatifs sont les forces de frottement, forces qui ne sont pas toujours définies simplement. Nous étudierons deux cas typiques que l’on rencontre souvent dans la pratique :

1. Force de frottement solide : en sens opposé de la vitesse et de grandeur indépendante de celle-ci ;

2. Force de frottement liquide (ou visqueux): en sens opposé de la vitesse et proportionnelle à celle-ci.

2. Amortissement par frottement solide

La force de frottement, en sens inverse du déplacement et d’une valeur constante \(F\) au cours du déplacement, s’ajoute à la résultante des forces appliquées.

Prenons comme force appliquée une force élastique : \(F=-k~x\). Supposons qu’à l’instant \(t=0\), l’élongation par rapport à la position d’équilibre soit \(x=a_0\) et la vitesse \(v=0\).

Naturellement, le mouvement ne peut se produire que si : \[k~a_0>F\qquad\text{soit :}\quad a_0>\frac{F}{k}\]

En vertu du principe de la dynamique, l’équation du mouvement s’écrit : \[m~\frac{d^2x}{dt^2}=-k~x+F\]

Moyennant d’un changement de variable : \[\frac{d^2X}{dt^2}~\frac{k}{m}~X=0\qquad\text{avec :}\quad X=x~\frac{F}{k}\]

Par intégration : \[X=A~\cos(\omega~t+\varphi)\]

Les constantes \(A\) et \(\varphi\) sont déterminées par les conditions initiales : \[t=0\quad;\quad x=a_0\quad;\quad v=0\]

D’où : \[v=-A~\omega~\sin\varphi=0\quad;\quad X_0=A~\cos\varphi=a_0-\frac{F}{k}\]

Deux possibilités :

\[\begin{aligned} &\varphi=2~K~\pi\quad\quad~~~\Rightarrow\quad~~\cos\varphi=1\quad\Rightarrow\quad A=a_0-\frac{F}{k}\\ &\varphi=\pi+2~K~\pi\quad\Rightarrow\quad\cos\varphi=-1\quad\Rightarrow\quad A=-\Big(a_0-\frac{F}{k}\Big)\end{aligned}\]

On aboutit à deux conditions identiques :

\[\begin{aligned} &[1]\qquad X=\Big(a_0-\frac{F}{k}\Big)~\cos\omega~t\\ &[2]\qquad X=-\Big(a_0-\frac{F}{k}\Big)~\cos(\omega~t+\varphi)=\Big(a_0-\frac{F}{k}\Big)~\cos\omega~t\end{aligned}\]

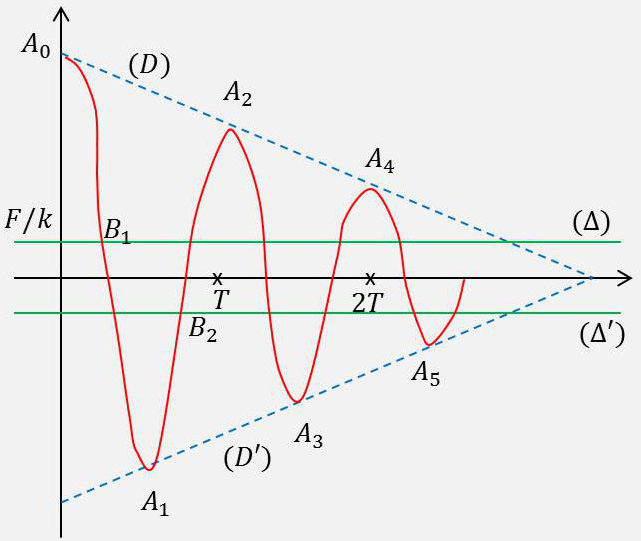
Le mouvement est donc unique et en définitive l’équation du mouvement à partir de l’instant \(t=0\) est : \[x=\frac{F}{k}+\Big(a_0-\frac{F}{k}\Big)~\cos\omega t~\]

La vitesse s’écrit alors : \[v=-\omega~\Big(a_0-\frac{F}{k}\Big)~\sin\omega~t\]

Elle redevient nulle pour : \[\omega~t=\pi\qquad\text{c-à-d :}\quad t=\frac{T}{2}\]

L’élongation correspondante est alors : \[x_1=-a_0+\frac{2~F}{k}=a_1\]

L’élongation correspondante est alors : \[x_1=-a_0+\frac{2~F}{k}=a_1\]

Entre \(t=0\) et \(t=T/2\) : \[x=\frac{F}{k}+\Big(a_0-\frac{F}{k}\Big)~\cos\omega~t\]

est représenté par l’arc de sinusoïde \(A_0B_1A_1\) de centre \(B_1\) avec : \[t=\frac{T}{4}\quad;\quad x=\frac{F}{k}\]

Supposons que : \[a_1<0\qquad\text{c-à-d :}\quad a_0>\frac{2~F}{k}\]

Le mobile \(A_1\) à l’instant \(T/2\) est soumis à la force élastique de grandeur \(k~a_1\) dirigée dans le sens \(A_{1,0}\). Celle-ci tend à ramener le point matériel vers sa position d’équilibre \(O\).

La force de frottement est dirigée en sens inverse du mouvement éventuel pour valeur maximale \(F\). Le mouvement vers les x positifs se produit si \(-k~a_1>F\).

L’équation différentielle du mouvement est, à partir de la position \(A_1\) : \[m~\frac{d^2x}{dt^2}=-k~x-F\]

ou encore : \[m~\frac{d^2}{dt^2}~\Big(x+\frac{F}{k}\Big)=-k~\Big(x+\frac{F}{k}\Big)\]

Par intégration : \[x+\frac{F}{k}=a'~\cos(\omega~t+\varphi')\quad;\quad v=-a'~\omega~\sin(\omega~t+\varphi')\]

On détermine les constantes par les conditions initiales : \[t=\frac{T}{2}~:\quad x=a_1\qquad;\qquad \omega~t=\pi~:\quad v=0\]

C’est-à-dire : \[a_1+\frac{F}{k}=-a'~\cos\varphi'\quad;\quad a'~\omega~\sin\varphi'\]

Deux possibilités :

\[\begin{aligned} &\varphi'=2~K~\pi\quad\qquad~\Rightarrow\quad\cos\varphi'=1\quad~~~\Rightarrow\quad a'=-a_1-\frac{F}{k}=a_0-\frac{3~F}{k}\\ &\varphi'=(2~K+1)~\pi\quad\Rightarrow\quad\cos\varphi'=-1\quad\Rightarrow\quad a'=a_1+\frac{F}{k}=-a_0+\frac{3~F}{k}\end{aligned}\]

Dans les deux cas, l’équation du mouvement à partir de \(A_1\) est : \[\left\{ \begin{aligned} &x=-\frac{F}{k}+\Big(a_0-\frac{3~F}{k}\Big)~\cos\omega~t\\ &v=\omega~\Big(\frac{3~F}{k}-a_0\Big)~\sin\omega~t \end{aligned} \right.\]

La vitesse redevient nulle à l’instant t tel que : \[\omega~t=2~\pi\quad\Rightarrow\quad t=T\]

Donc, de l’instant \(T/2\) à l’instant \(T\), la courbe représentative du mouvement est l’arc de sinusoïde \(A_1B_2A_2\) de centre \(B_2\) (\(t=3T/4~;~x=-F/k\)) se raccordant à l’instant \(T/2\) à l’arc de sinusoïde \(A_0B_1A_1\).

À l’instant T, on a : \[x=a_0-\frac{4~F}{k}\]

En définitive, le mouvement est représenté par des arcs de sinusoïde se raccordant aux instants \(T/2,~2T/2,~3T/2,~\dots\) aux points d’élongation : \[a_0,~-\Big(a_0-\frac{2~F}{k}\Big),~\Big(a_0-\frac{4~F}{k}\Big),~\dots\]

Les amplitudes d’un même côté de la position d’équilibre diminuent en progression arithmétique de raison \(4~F/k\).

Les points d’accélération nulle sont situés alternativement sur les droites : \[(\Delta)~:\quad x=\frac{F}{k}\quad;\quad (\Delta')~:\quad x=-\frac{F}{k}\]

et les points de vitesse nulle alternativement sur les droites \((D)\) et \((D')\).

L’arrêt se produit lorsque, à vitesse nulle, la force de frottement maximale \(F\) est supérieure à la force élastique correspondante : \[\frac{K}{k}>|a_1|\]

c’est-à-dire lorsque le point de vitesse nulle est situé entre les droites : \[(\Delta),~(\Delta')~:\quad x=\pm\frac{F}{k}\]

Comme d’autre part les points de vitesse nulle sont situés sur les droites \((D)\) et \((D')\), cherchons l’abscisse commune des points \(C\) et \(C'\) de rencontre des droites \(\Delta\) et \(D\) ou des droites \(\Delta'\) et \(D'\) : \[a_0-4~\frac{\tau}{T}~\frac{F}{k}=\frac{F}{k}\qquad\Rightarrow\qquad\tau=\Big(\frac{a_0-F/k}{F/k}\Big)~\frac{T}{4}\]

L’arrêt se produit au temps \(m~T/2\), entier immédiatement supérieur au temps \(\tau\) : \[m~\geq~\frac{1}{2}~\Big(\frac{a_0-F/k}{F/k}\Big)=\frac{1}{2}~\Big(\frac{k~a_0}{F}-1\Big)\]

L’élongation correspondante, comprise entre \(F/k\) et \(-F/k\) a pour valeur : \[x=(-1)^m~\Big(a_0-2~m~\frac{F}{k}\Big)\]

La position d’arrêt est conditionnée par le rapport \(k~a_0/F\) de la force élastique initiale et à la force de frottement solide, soit pour une raideur \(k\) et un frottement solide \(F\) donnés, par la valeur de l’élongation initiale \(a_0\).

Application

Soit à trouver la position d’équilibre de la partie mobile d’un appareil de mesure. Le frottement des pivots laisse indéterminée la position d’arrêt d’une quantité \(\pm\varepsilon\) sans que nous ayons la possibilité de connaître la grandeur et le sens de l’erreur.

Il y a donc lieu pour tous les appareils de mesure comportant une partie mobile susceptible d’un frottement solide de réduire ce frottement à une valeur aussi petite que possible et d’augmenter la raideur \(k\) de l’oscillateur (ce qui revient à augmenter sa fréquence) de manière que l’erreur commise, provenant de l’indétermination du point d’arrêt, soit inférieure à la plus petite élongation que l’on peut apprécier.

Sinon, il y aura la possibilité de recommencer de nombreuses fois l’essai (en agitant l’appareil par exemple s’il est robuste) et chercher autour de quel point se répartissent les positions d’arrêt.

3. Amortissement par frottement visqueux

Dans le cas d’un frottement visqueux, la force de frottement est maintenant proportionnelle à la vitesse, soit : \[F=-f~v=-f~\frac{dx}{dt}\quad;\quad f>0\]

L’équation différentielle du mouvement s’écrit : \[m~\frac{d^2x}{dt^2}+f~\frac{dx}{dt}+k~x=0\]

Posons : \[\frac{f}{m}=2~\alpha~\omega_0\qquad\text{et}\qquad \omega_0^2=\frac{k}{m}\]

\(\omega_0\) serait l’amortissement si le pendule n’était pas amorti ; \(\alpha\) caractérise l’amortissement.

L’équation différentielle devient : \[\frac{d^2x}{dt^2}+2~\alpha~\omega_0~\frac{dx}{dt}+\omega_0^2~x=0\]

On sait qu’il faut chercher des solutions de la forme \(x=\exp(r~t)\), d’où : \[\exp(r~t)~(r^2+2~\alpha~\omega_0~r+\omega_0^2)=0\]

\(r\) est donné par l’équation (caractéristique) du second degré pour laquelle : \[\Delta'=\omega_0^2~(\alpha^2-1)\]

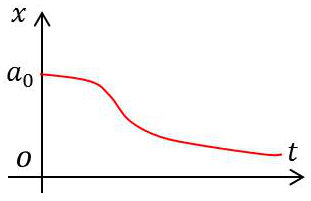
3.1. Amortissements forts (\(\alpha>1)\)

Il y a deux racines réelles négatives. La solution générale est donc : \[x_1=A~\exp(r_1~t)+B~\exp(r_2~t)\quad;\quad r_1,~r_2<0\]

A et B sont déterminées par les conditions initiales.

Faisant \(t=0,~v=0\), on voit que A et B sont de signes contraires.

Supposons, pour fixer les idées que : \(|r_1|>|r_2|\). Au bout d’un certain temps : \(x\approx B~\exp(r_2~t)\), donc \(x\rightarrow 0\) quand \(t\rightarrow 0\) et le mouvement est apériodique.

Cependant \(x\) ne peut s’annuler pour un temps infini. En effet : \[|r_1|>|r_2|\quad\Rightarrow\quad |r_1~A_1|>|r_2~A_2|\]

On doit donc avoir \(|B|>|A|\).

Comme \(A+B=a_0>0\), donc \(B>0\) et \(A<0\).

On a constamment : \[|B~\exp(r_2~t)|>|A~\exp(r_1~t)|\quad\Rightarrow\quad x>0\]

3.2. Amortissement critique (\(\alpha = 1\))

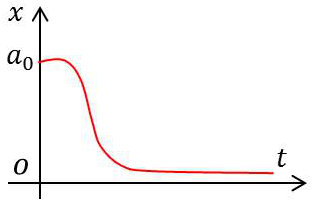Pour l’amortissement critique, on a \(\Delta'=0\).

L’équation possède une racine double \(r=-\alpha~\omega_0\).

D’où la solution : \[x=\exp(r~t)(A+B~t)=\exp(-\alpha~\omega_0~t)~(A+B~t)\]

On voit que \(x~\rightarrow 0\) quand \(t~\rightarrow\infty\). On dit que le mouvement est critique.

3.3. Mouvement sinusoïdal amorti (a < 1)

Quand le mouvement est amorti, on a \(\Delta'<0\).

Deux racines complexes conjuguées : \[(r_1,~r_2)=-\alpha~\omega\pm j~\omega\quad;\quad\omega=\omega_0~\sqrt{1-\alpha^2}\]

La solution générale de l’équation est : \[x=\exp(-\alpha~\omega_0~t)~(A~\cos\omega~t+B~\sin\omega~t)\]

Solution qui peut être mise sous la forme : \[x=\exp(-\alpha~\omega_0~t)~\sin(\omega~t+\varphi)\quad;\quad (a,~\varphi)~ctes\]

Ce mouvement n’est pas en toute rigueur oscillatoire. On le désigne sous le nom de mouvement sinusoïdal amorti.

On peut toujours choisir l’origine des temps de sorte que \(\varphi=0\). Nous avons toujours : \[|x|\leq a\exp(-\alpha~\omega_0~t)\]

On aura donc :

\[\begin{aligned} &x=a~\exp(-\alpha~\omega_0~t)~~\text{pour}~~\sin\omega t=1\quad\quad~\text{c-à-d :}\quad t_1=\frac{\pi}{2~\omega}+\frac{2~K~\pi}{\omega}\\ &x=-a~\exp(-\alpha~\omega_0~t)~~\text{pour}~~\sin\omega t=-1\quad\text{c-à-d :}\quad t_1=-\frac{\pi}{2~\omega}+\frac{2~K~\pi}{\omega}\end{aligned}\]

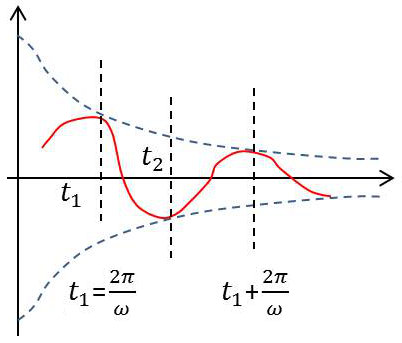
La courbe d’équation : \(x=a~\exp(-\alpha~\omega_0~t)~\sin\omega~t \)

est tangente aux exponentielles : \(x=a~\exp(-\alpha~\omega_0~t) \)

aux points d’abscisses \(t_1,~t_1+\cfrac{2~\pi}{\omega},~\dots\)

et tangente aux exponentielles : \(x=-a\exp(-\alpha~\omega_0~t)\)

aux points d’abscisses \(t_1+\cfrac{\pi}{\omega}~,~t_1+\cfrac{3~\pi}{\omega},~\dots\)

On dérive par rapport au temps pour obtenir la vitesse. On trouve que : \[v=0\quad\text{pour :}\quad \tan\omega~t=\frac{\omega}{\alpha~\omega_0}=\frac{\sqrt{1-\alpha^2}}{\alpha}\]

C’est-à-dire pour : \[\sin\omega~t=\pm\sqrt{1-\alpha^2}\quad\Rightarrow\quad\omega~t=\pm \arcsin\sqrt{1-\alpha^2}\]

Si \(a\) est petit, \(v=0\) pour : \(\omega~t\cong\pi/2\).

Partant de la relation : \[\omega~t=\pm\arcsin\sqrt{1-\alpha^2}\]

on peut écrire : \[x=\pm a~\sqrt{1-\alpha^2}~\exp(-\alpha~\omega_0~t)\]

On voit alors que les maximums et les minimums se placent respectivement :

• sur l’exponentielle affine de \(x=a~\exp(-\alpha~\omega_0~t)\) dans le rapport \(\sqrt{1-\alpha^2}\) ;

• sur l’exponentielle affine de \(x=-a~\exp(-\alpha~\omega_0~t)\) dans le même rapport.

3.3.1. Pseudo-période

On appelle pseudo-période l’intervalle de temps séparant 2 élongations, nulles ou maximum : \[T=\frac{2~\pi}{\omega}=\frac{2~\pi}{\omega_0~\sqrt{1-\alpha^2}}=\frac{T_0}{\sqrt{1-\alpha^2}}\]

\(T_0\) : période qu’aurait l’oscillateur en l’absence de frottement.

3.3.2. Décrément logarithmique

Soient 2 élongations maximales successives :

\[\begin{aligned} &x_n=a~\sqrt{1-\alpha^2}~\exp\big\{-\alpha~\omega_0~t_n\big\}\\ &x_{n+1}=a~\sqrt{1-\alpha^2}~\exp\big\{-\alpha~\omega_0~\Big(t_n+\frac{2~\pi}{\omega}\Big)\big\}\end{aligned}\]

Il vient : \[\frac{x_n}{x_{n+1}}=\exp\Big(\alpha~\omega_0~\frac{2~\pi}{\omega}\Big)=\exp(\alpha~\omega_0~T)\]

On désigne sous le nom de décrément logarithmique la quantité : \[\delta=\ln\frac{x_n}{x_{n+1}}\]

On a donc : \[\delta=\alpha~\omega_0~T=2~\pi~\alpha~\frac{\omega_0}{\omega}=\frac{2~\pi~\alpha}{\sqrt{1-\alpha^2}}\]

Soit finalement : \[\delta\cong 2~\pi~\alpha\quad\text{dans le cas où}~~\alpha\ll 1\]

3.3.3. Constante de temps de l’oscillateur

Posons : \[\alpha~\omega_0=\frac{1}{\theta}\quad\text{ou}\quad\frac{\delta}{T}=\frac{1}{\theta}\]

\(\theta\) : constante de temps de l’oscillateur.

L’équation du mouvement devient alors : \[x=a~\exp\Big(-\frac{t}{\theta}\Big)~\sin(\omega~t+\varphi)\]

\(\theta\) est l’intervalle de temps au bout duquel l’amplitude a été divisée par \(e\).

3.3.4. Ordre de grandeur de la variation de période

Cette variation de période est introduite par l’amortissement. Considérons une oscillation très amortie, où l’amplitude est divisée par \(e\) à chaque oscillation.

On a alors : \[\theta=T\quad\Rightarrow\quad \delta=1\]

D’autre part : \[T=\frac{T_0}{\sqrt{1-\cfrac{\delta^2}{4~\pi^2}}}\approx T_0~\Big(1+\frac{\delta^2}{8~\pi^2}\Big)\]

En particulier : \[\delta=1\quad\Rightarrow\quad T=T_0~\Big(1+\frac{1}{80}\Big)\]

Ainsi, \(\Delta T/T_0=1,25~\%\) seulement, bien que l’amortissement soit considérable.

3.3.5. Points de vitesse nulle

Par extension au plan complexe, on peut représenter l’équation du mouvement par : \[\left\{ \begin{aligned} &z=a~\exp(-\alpha~\omega_0~t)~\exp[j~(\omega t+\varphi)]\\ &\rho=a~\exp(-\alpha~\omega_0~t)\quad;\quad\theta=\omega~t+\varphi \end{aligned} \right.\]

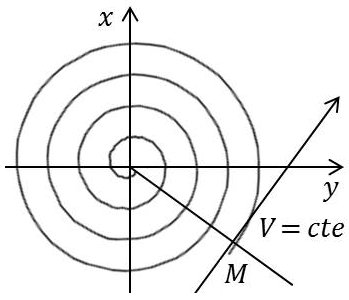On reconnaît l’équation polaire de la spirale logarithmique dont on rappelle la propriété essentielle : la courbe s’enroule autour du point asymptote et coupe tout rayon vecteur sous un angle constant \(V\).

On sait que : \[\tan V=\frac{d\rho}{\cfrac{d\rho}{d\theta}}=\rho~\frac{d\theta}{d\rho}=\omega~\rho~\frac{dt}{d\rho}\]

Or, on a par ailleurs : \[\frac{d\rho}{dt}=-\alpha~\omega_0~\rho\quad\Rightarrow\quad\tan V=\frac{\omega}{\alpha~\omega_0}\]

Soit encore : \[\beta=V-\frac{\pi}{2}\quad\Rightarrow\quad \tan\beta=\frac{\alpha~\omega_0}{\omega}=cte\]

La droite qui fait cet angle avec le rayon vecteur coupe la spirale en un point à tangente horizontale : l’oscillateur a alors une vitesse nulle.

3.4. Analogie électrique

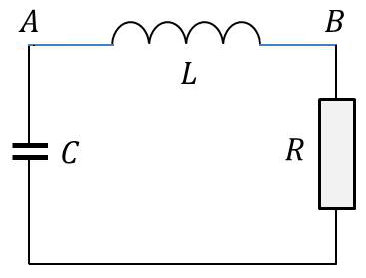Nous obtiendrons l’analogie électrique en intercalant une résistance ohmique dans le circuit oscillant du précédent chapitre.

\[\begin{aligned} V_A-V_B&=L~\frac{di}{dt}=L~\frac{d^2q}{dt^2}\\ V_B-V_C&=R~i=R~\frac{dq}{dt}\\ V_C-V_A&=\frac{q}{C}\end{aligned}\]

En faisant la somme : \[L~\frac{d^2q}{dt^2}+R~\frac{dq}{dt}+\frac{q}{C}=0\]

En notant que \(V=q/C\) : \[\frac{d^2V}{dt^2}+\frac{R}{L}~\frac{dV}{dt}+\frac{1}{L~C}~V=0\]

On pose généralement : \[\frac{R}{L}=2~\alpha~\omega_0\quad;\quad \frac{1}{L~C}=\omega_0^2\]

Discussion

• \(\alpha>1\) : Mouvement apériodique \[\frac{R}{2~L~\omega_0}>1\quad\text{ou}\quad \frac{L~\omega_0}{R}<\frac{1}{2}\]

  Cette dernière quantité est la surtension ou l’acuité de résonance.

• \(\alpha=1\) : Mouvement apériodique \[\frac{L~\omega_0}{R}=\frac{1}{2}\]

• \(\alpha<1\) : Mouvement oscillatoire amorti \[\frac{L~\omega_0}{R}>\frac{1}{2}\]

Les relations de solution sont identiques aux précédentes (mécaniques) à savoir :

• Équation du mouvement : \[x=a~\exp(-\alpha~\omega_0~t)~\cos(\omega~t+\varphi)\]

• Décrément logarithmique : \[\delta~\cong~2~\pi~\alpha\]

• Constante de temps : \[\theta=\frac{1}{\alpha~\omega_0}=\frac{2~L}{R}\]