1. Effet Compton
1.1. Constat de la relativité restreinte
L’énergie d’un photon \(X\) est :\(W~=~h\nu\)
Le photon est une particule dont la masse au repos a pour valeur :\(m_0~=~0\)
La relativité restreinte a introduit la relation : \[m~=~\frac{m_0}{\sqrt{1-\cfrac{v^2}{c^2}}}\]
-
Première interprétation :
-
la masse du photon devient finie pour \(v=c\).
-
-
Deuxième interprétation :
-
le photon ne se manifeste que si sa vitesse est celle de la lumière ;
-
son énergie \(m~c^2\) devient finie.
-
1.2. Une expérience
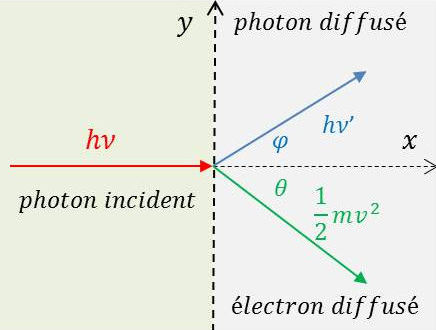 Un photon vient frapper un électron au repos en \(O\).
Un photon vient frapper un électron au repos en \(O\).
Après le choc, le photon est diffusé suivant une direction \(\varphi\) et son énergie devient \(h~\nu'\).
L’électron est diffusé suivant une direction \(\theta\).
1) Si la vitesse de l’électron est \(v\ll c\)}, celui-ci va acquérir une énergie cinétique : \[\Delta E~=~\frac{1}{2}~m~v^2\]
Et d’après le principe de conservation de l’énergie : \[h~\nu~=~h~\nu'+\frac{1}{2}~m~v^2\qquad(1)\]
2) Si la vitesse \(v\) de l’électron n’est plus négligeable vis-à-vis de \(c\), la théorie de la relativité a montré que la variation d’énergie est : \[\Delta E~=~(m-m_0)~c^2\]
D’après le principe de conservation de l’énergie : \[h~\nu~=~h~\nu'+m~c^2-m_0~c^2\qquad(2)\]
La quantité de mouvement d’un photon est : \[p~=~\frac{m~c^2}{c}~=~\frac{h~\nu}{c}\]
D’après le principe de conservation de la quantité de mouvement (en projections) : \[\begin{aligned} /Ox~&:\quad &&\frac{h~\nu}{c}=\frac{h~\nu'}{c}~\cos\varphi~+~m~v\cos\theta\qquad(3)\\ /Oy~&: &&~~~~0=\frac{h~\nu'}{c}\sin\varphi~-~m~v~\sin\theta\qquad(4) \end{aligned}\]
De ces deux relations, on tire :
\[\begin{aligned} \cos\theta~&=~\frac{1}{m~v}~\Big(\frac{h~\nu}{c}-\frac{h~\nu'}{c}\Big)~\cos\varphi\\ \sin\theta~&=~\frac{1}{m~v}~\Big(\frac{h~\nu'}{c}\Big)~\sin\varphi\end{aligned}\]
En écrivant que : \[\sin^2\theta+\cos^2\theta=1\]
on élimine \(\theta\), de sorte que : \[m^2~v^2~=~\frac{h^2~\nu^2}{c^2}+\frac{h^2~\nu'^2}{c^2}-\frac{2~h^2~\nu~\nu'}{c^2}~\cos\varphi\qquad(5)\]
De la relation (2), on tire : \[m^2~=~\Big\{\frac{h~(\nu-\nu')}{c^2}+m_0\Big\}^2\]
D’autre part : \[m~=~\frac{m_0}{\sqrt{1-\cfrac{v^2}{c^2}}}\qquad\Rightarrow\qquad m^2~v^2=m^2~c^2-m_o^2~c^2\]
On obtient donc :
\[\begin{aligned} m^2~v^2~&=~c^2~\Big\{\frac{h~(\nu-\nu')}{c^2}+m_0\Big\}-m_0^2~c^2\\ m^2~v^2~&=~\frac{h^2~\nu^2}{c^2}+\frac{h^2~\nu'^2}{c^2}-\frac{2~h^2~\nu~\nu'}{c^2}+2~h~(\nu-\nu')~m_0\qquad(6)\end{aligned}\]
En identifiant (5) et (6) : \[-\frac{2~h^2~\nu~\nu'}{c^2}~\cos\varphi~=~-\frac{2~h^2~\nu~\nu'}{c^2}+~2h~(\nu-\nu')~m_0\]
En introduisant la simplification : \[\frac{h}{c^2}~\nu~\nu'~(1-\cos\varphi)~=~(\nu-\nu')~m_0\]
On obtient ainsi : \[\lambda'-\lambda~=~\frac{c}{\nu}-\frac{c}{\nu'}~=~\frac{1}{m_0~c}~(1-\cos\varphi)\qquad(7)\]
Le facteur : \[\lambda_c~=~\frac{1}{m_e~c}\qquad (m_0~\rightarrow~m_e)\]
est appelé longueur d’onde Compton : \[\lambda_c~\approx~2,4\times 10^{12}~\rm m = 2,4~pm\]
L’effet Compton représente un premier moyen de détection des particules. La connaissance de \(\nu\) entraine celle de \(\nu'(\varphi)\). Il suffit de déterminer l’angle \(\varphi\) avec un compteur recevant le photon diffusé. De la même façon pour \(v(\theta)\).
2. Effet photoélectrique
L’effet photoélectrique peut se présenter comme une suite logique de l’effet Compton.
Cette fois des électrons sont émis par un matériau exposé à la lumière ou à un rayonnement électromagnétique de fréquence suffisamment élevée et fonction de ce matériau.
2.1. Principe
L’énergie d’un faisceau est uniformément répartie sur tout le front d’onde. Plus cette lumière est intense, plus les amplitudes des champs électrique et magnétique en chaque point du front d’onde le seront.
Ces champs exercent sur les électrons d’un métal des forces capables d’en arracher certains de sa surface.
2.2. Conditions d’émission
L’émission d’électrons (photoélectrons) n’est possible que si la fréquence de la lumière dépasse une fréquence limite. Cette fréquence seuil dépend du matériau, directement liée à l’énergie de liaison des électrons qui peuvent être émis.
Le nombre d’électrons émis lors de l’exposition à la lumière (intensité du courant électrique), est proportionnel à l’intensité de la source lumineuse.
Leur vitesse est indépendante de l’intensité de la source lumineuse.
Leur énergie cinétique dépend linéairement de la fréquence de la lumière incidente.
Le phénomène est quasi instantané (\(\tau~\leq~10^{-9}~\rm s\)).
2.3. Discussion
1) Si l’énergie du photon incident est inférieure à l’énergie de liaison \(E_l\) de l’électron K, l’effet photoélectrique se fait avec un électron de la couche L, etc.
2) Si le rayonnement est absorbé, l’atome est excité : son état d’énergie n’est pas l’état minimal.
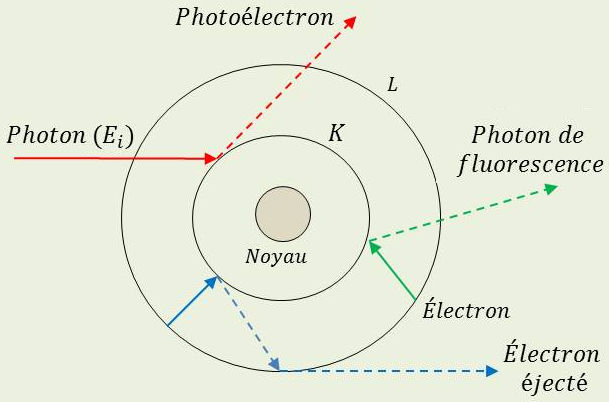 Il s’ensuit une relaxation (ou désexcitation): un électron d’une couche supérieure vient combler la case quantique laissée vacante par l’électron éjecté.
Il s’ensuit une relaxation (ou désexcitation): un électron d’une couche supérieure vient combler la case quantique laissée vacante par l’électron éjecté.
3) Si l’énergie de transition est modérée (le rayonnement incident d’énergie modérée), la relaxation provoque l’émission d’un photon de faible énergie (visible ou ultra-violet) : c’est le phénomène de fluorescence.
4) Si l’énergie de transition est élevée, deux cas peuvent se produire :
-
émission d’un photon fluorescent (photon X du fait de son énergie) ;
-
capture possible de ce photon X de nouveau par l’atome lui-même et éjection d’un électron périphérique.
Après l’absorption du photon par l’atome, le photoélectron émis a une énergie : \[E_{pe}= E_i - E_l\qquad (E_l~\text{énergie de liaison du photoélectron})\]
L’effet photoélectrique domine aux faibles énergies, mais la section efficace croît rapidement avec le numéro atomique \(Z\) : \[\sigma_{pe}~=~\frac{Z^n}{{E_i}^{3,5}}\qquad~n\in\{4~;~5\}\]
2.4. Calculs pratiques
Un faisceau éclaire la cathode d’une cellule photoélectrique.
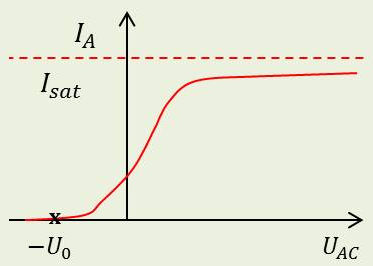 1) L’intensité \(I_A\) en fonction de la différence de potentiel anode – cathode présente la caractéristique ci-contre : \[U_{AC}~=~U_A-U_C\qquad U_0~:~\text{potentiel d'arrêt }\]
1) L’intensité \(I_A\) en fonction de la différence de potentiel anode – cathode présente la caractéristique ci-contre : \[U_{AC}~=~U_A-U_C\qquad U_0~:~\text{potentiel d'arrêt }\]
2) Travail d’extraction de l’électron pour fréquence seuil \(\nu_0\) de la cellule : \[W_0~=~h~\nu_0\]
3) Vitesse de l’électron en sortie de cathode (longueur d’onde de radiation émise \(\lambda\))
Énergie photonique : \[E_{ph}~=~h~\nu~=~\frac{h~c}{\lambda}\]
À partir de l’énergie cinétique :
\[\begin{aligned} E_c~&=~\frac{1}{2}~m~v^2~=~E_{ph}-W_0\\ v^2~&=~\frac{2~(E_{ph}-W_0)}{m_e}\qquad\Rightarrow\qquad v~=~\sqrt{\frac{2~(E_{ph}-W_0)}{m_e}}\end{aligned}\]
4) Vitesse de l’électron quand il arrive sur l’anode (\(U\) : d.d.p. accélératrice)
Travail électrique appliqué : \[W~=~e~U\]
Application du théorème de l’énergie cinétique :
\[\begin{aligned} E_{c,an}-E_{c,cat}~&=~e~U\\ E_{c,an}~&=~E_{c,cat}+e~U~=~(E_{ph}-W_0)+e~U\\ E_{c,an}~&=~\frac{1}{2}~m_e~v_{an}^2\qquad\Rightarrow\qquad v_{an}=\sqrt{\frac{2~E_{c,an}}{m_e}}\end{aligned}\]
5) Relation entre le rendement quantique \(\rho\), la puissance lumineuse reçue \(P\) par la cathode et le courant de saturation \(I_{sat}\)
Rendement quantique : \[\rho~=~\frac{n}{N}=\frac{\text{nbre photons efficaces (qui arrachent les électrons})}{\text{nbre total de photons (reçus par la cathode})}\]
Nombres de photons reçus pendant un temps élémentaire \(\Delta t\) : \[n~=~\frac{I_{sat}~\Delta t}{e}\qquad;\qquad N~=~\frac{P~\Delta t}{h~\nu}\]
On a donc : \[\rho~=~\frac{I_{sat}~\Delta t~h~\nu}{P~\Delta t~e}\qquad\Rightarrow\qquad I_{sat}~=~\frac{\rho~P~e}{h~\nu}\]
Constantes utiles \[\left\{ \begin{aligned} e&=1,6\times 10^{-19}~\rm C && 1~eV=1,6\times 10^{-19}~J\\ \quad m_e&=9,1\times 10^{-31}~\rm kg\\ h&=6,63\times 10^{-34}~{\rm J~s}\qquad &&\quad c=3\times 10^8~\rm m~s^{-1} \end{aligned} \right.\]
3. Einstein et l’effet photoélectrique
En 1900, Max Planck annonçait : La chaleur irradiée n’est pas un flux continu et indéfiniment divisible. Ce flux peut se définir comme étant une masse discontinue composée d’éléments similaires les uns aux autres.
En 1905, Einstein ira plus loin : Les gains de lumière (futurs photons) qui accompagnent les ondes lumineuses cèdent leur énergie aux électrons en les libérant des corps frappés par des rayons lumineux cette énergie étant fonction de la fréquence.
La notion de quanta de lumière ainsi introduite expliquait le phénomène de la photoélectricité. Cette idée d’Einstein se trouva à l’origine de la mécanique ondulatoire.
Louis de Broglie reconnaissait lui-même : Je fus convaincu que le dualisme des ondes et des corpuscules découvert par Einstein dans sa théorie des quanta de lumière était absolument général et s’étendait à toute la nature physique et il me parut dès lors certain qu’au mouvement d’un corpuscule quelconque, qu’il soit photon,électron, proton ou autre, est associée la propagation d’une onde.
Ainsi, c’est à la suite de ses mesures quantitatives de l’effet photoélectrique (domaine de sa thèse de doctorat) qu’Einstein avait proposé, dès 1905, d’attribuer à la théorie quantique de la lumière sa justification : une explication théorique qui sera en grande partie à l’origine de son prix Nobel en 1921.

