1. Modèle simple de l’atome.
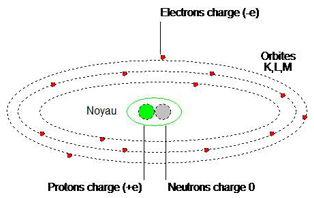 La structure élémentaire du cortège électronique autour du noyau (cas de la structure dite non fine) est bien connue.
La structure élémentaire du cortège électronique autour du noyau (cas de la structure dite non fine) est bien connue.
Pour mémoire, les nombres d’électrons des couches en saturation : K (2 électrons), L (8), M (8), etc.
Exemples du carbone, du silicium et du soufre : \[\begin{array}{ccc} \text{Atome} &\text{Électrons} &\text{Répartition}\\ \rm C &6 &\rm K^2L^4\\ \rm Si &14 &\rm K^2L^8M^4\\ \rm S &16 &\rm K^2L^8M^6 \end{array}\]
L’atome est électriquement neutre : il y a donc autant de protons [charge (+e)] que d’électrons [charge (–e)].
Valeurs de ces masses élémentaires :
\[\begin{aligned} &m_p=1,673~\times~10^{-27}~{\rm kg}\quad;\quad m_n=1,675\times 10^{-27}~\rm kg\\ &m_p\approx m_n\approx 1,67\times 10^{-27}~\rm kg\\ &m_p\approx m_n\approx 1840~m_e\end{aligned}\]
L’unité de masse atomique (1/12 de la masse de l’atome de carbone 12, pris comme référence) a pour valeur : \[1~\rm u=1,660540\times 10^{-27}~kg\]
Elle est très pratique en raison des très petites valeurs, donc avec des exposants souvent importants à manipuler.
Ainsi, pour le proton, le neutron et l’électron :
\[\begin{aligned} m_p&=1,00728~\rm u\\ m_n&=1,00866~\rm u\\ m_e&=0,00055~\rm u\end{aligned}\]
On rappelle l’écriture symbolique d’un élément \(X\) ayant \(Z\) protons et \(N\) neutrons : \[~_Z^AX\]
Avec :
-
A : nombre de masse (somme des nucléons)\(\qquad A=Z+N\)
-
Z : nombre de charge (nombre de protons ou d’électrons)
1.1. Isobares et isotopes
Deux éléments de nombres \(A\) identiques sont appelés isobares.
Deux éléments de nombres \(Z\) identiques, mais différents en \(N\) et par suite en \(A\), sont appelés isotopes ou encore nucléides. Ces atomes identiques sont seulement différenciés par les neutrons du noyau, une différenciation d’origines naturelle ou artificielle (réaction nucléaire).
1.2. Exemples classiques d’isotopes
Hydrogène, deutérium (eau lourde – cf. note in fine) et tritium : \[~_1^1\rm H\quad;\quad~_1^2H\quad;\quad~_1^3H\]
Pour ces deux derniers isotopes, on peut trouver les notations respectives D et T.
Carbone : \(~^{14}\rm C\) (pour les opérations de datation) \[~6^{12}\rm C\quad;\quad~_6^{13}C\quad;\quad~_6^{14}C\]
Uranium : \[~_{92}^{235}\rm U\quad;\quad~_{92}^{238}U\]
2. Radioactivité
Un noyau possédant trop de particules de même type (proton ou neutron) est instable. Il ne peut parvenir à cette stabilité qu’en se libérant, d’une manière ou d’une autre, de cet excès de particules.
Deux interactions entre en jeu dans la stabilité d’un noyau :
-
une interaction forte, à l’origine de l’attraction entre nucléons ;
-
une interaction magnétique, à l’origine de la répulsion entre protons.
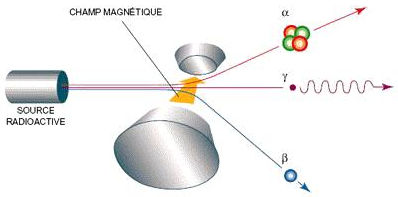 Lorsqu’un noyau \(X\) est instable, il subit une transformation spontanée qui aboutit à la formation d’un nouveau noyau \(Y\) : \[~_Z^AX\quad\Rightarrow\quad~_{Z'}^{A'}\]
Lorsqu’un noyau \(X\) est instable, il subit une transformation spontanée qui aboutit à la formation d’un nouveau noyau \(Y\) : \[~_Z^AX\quad\Rightarrow\quad~_{Z'}^{A'}\]
La transformation s’accompagne de l’émission de particules et de rayonnements électromagnétiques.
La charge électrique et le nombre de nucléons sont conservés au cours d’une telle réaction.
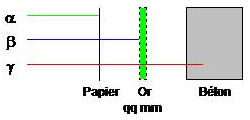 Effets biologiques
Effets biologiques
-
Les rayons \(\alpha\) sont peu pénétrants, mais très ionisants.
-
Les rayons \(\beta\) sont assez pénétrants et peu ionisants.
-
Les rayons \(\gamma\) sont très pénétrants, mais peu ionisants.
Remarque
L’unité d’énergie souvent utilisée en physique nucléaire est l’électronvolt (eV). Rappelons que c’est l’énergie acquise par une charge élémentaire soumise à une différence de potentiel de 1 V (loi de Coulomb) : \[1~\rm eV=1,60217733\times 10^{-19}~J\]
3. Vue synthétique des quatre types de rayonnement
3.1. Radioactivité \(\alpha\)
Quand l’instabilité est due à un excès de nucléons, un noyau d’hélium est émis : \[~_Z^AX\quad\rightarrow\quad~_{Z-2}^{A-4}Y~+~~_4^2He\]
Exemple du radium mué en radon : \[~_{88}^{226}\rm Ra\quad\rightarrow\quad~_{86}^{222}Rn~+~~_2^4He\]
3.2. Radioactivité \(\beta^-\)
Quand l’instabilité est due à un excès de neutrons, un neutron se transforme en proton et un électron est émis : \[~_0^1\rm n\quad\rightarrow\quad~_1^1p~+~~_{-1}^{~~0}e\]
D’où l’équation de la réaction : \[~_Z^AX\quad\rightarrow\quad~_{Z+1}^AY~+~~_{-1}^{~~0}e~+~\bar{\nu}\]
\(\bar{\nu}\) : antineutrino
Exemple du carbone 14 : \[~_6^{14}\rm C\quad\rightarrow\quad~_7^{14}N~+~~_{-1}^{~~0}e\]
3.3. Radioactivité \(\beta^+\)
Quand l’instabilité est due à un excès de protons, un proton se transforme en un neutron et un positon : \[~1^1p\quad\rightarrow\quad~_{Z-1}^AY~+~~_1^0e~+~\nu\]
Le positon est une particule de même masse que l’électron, mais de charge opposée [+e].
3.4. Radioactivité \(\gamma\)
La radioactivité \(gamma\) accompagne la désintégration \(\alpha\) ou \(\beta\). Le noyau issu de la désintégration est souvent dans un état instable ou excité ; il devient stable en libérant un excédent d’énergie sous forme de rayonnement \(\gamma\) de très faible longueur d’onde (\(\lambda~<~10^{-12}~\rm m\)).
4. Noyaux stables et noyaux instables
On classe les éléments présents dans la nature en deux catégories :
-
ceux dont les noyaux ne subissent au cours du temps aucune transformation ;
-
ceux dont les noyaux émettent un rayonnement à un moment de leur existence.
Parmi les 1500 nucléides connus, il en existe environ 325 naturels, dont 274 sont stables, et 51 instables ou radioactifs. Le noyau de ces derniers est susceptible à tout moment de subir un changement pouvant porter sur le nombre de masse \(A\), sur le nombre de charge \(Z\) ou sur ces deux valeurs.
Si l’on classe ces nucléides stables en fonction des nombres A et Z qui les caractérisent, on peut faire apparaître une zone dite vallée de stabilité.
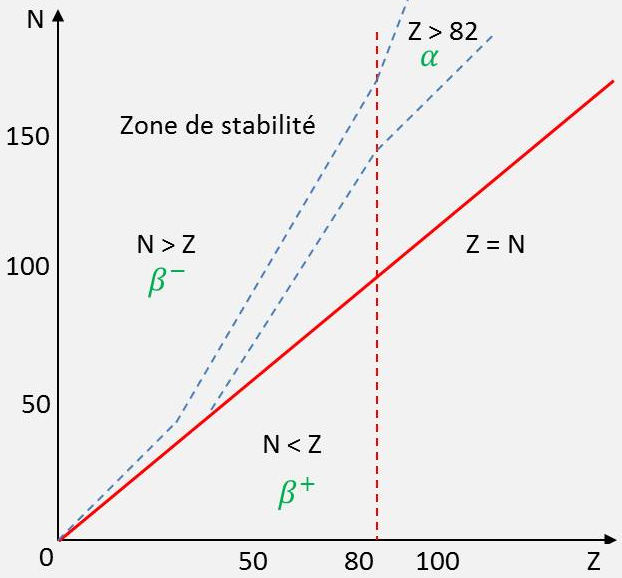 Le diagramme indique le nombre \(N\) de neutrons du nucléide en fonction du nombre de charge Z. Il comporte également le tracé de la bissectrice \(N = Z\) et de la zone de stabilité.
Le diagramme indique le nombre \(N\) de neutrons du nucléide en fonction du nombre de charge Z. Il comporte également le tracé de la bissectrice \(N = Z\) et de la zone de stabilité.
Pour \(A\) < 20, pratiquement tous ces nucléides vérifient la relation approchée \(A = 2~Z\), c’est-à-dire \(N = Z\). Ainsi, un noyau stable pour lequel A < 20 possède pratiquement autant de protons que de neutrons.
Pour \(A\) > 20, les noyaux stables ont un excès de neutrons. Le rapport \(A/Z\) augmente pratiquement avec \(A\) et tend vers 2,5 pour les noyaux les plus lourds.
Dans les deux cas, les noyaux instables radioactifs s’écartent légèrement de la vallée de stabilité. Ces nucléides possèdent un excès ou un défaut de neutrons.
Au-delà du dernier nucléide stable (Z = 82), ces nucléides possèdent un excès de nucléons. Ce sont des noyaux lourds.
5. Une modélisation de la vallée de stabilité
La formule dite de Bethe-Weizsäcker permet de décrire la vallée de stabilité. Cette formule semi-empirique exprime la valeur de l’énergie \(B\) de liaison entre les nucléons constituant le noyau.
5.1. Expression de la formule de Bethe-Weizsäker
Cinq énergies contribuent à l’énergie \(B\) de liaison entre les nucléons : \[B(A,Z)=E_v+E_s+E_c+E_a+E_p\]
Les deux première sont les énergies respectivement de volume \(E_v\) et de surface \(E_s\). Elles sont décrites par le modèle dit de la goutte liquide du noyau.
La troisième \(E_c\) est une énergie de répulsion électrostatique entre les protons.
Les deux dernières énergie, l’énergie d’asymétrie \(E_a\) et l’énergie d’appariement \(E_p\), sont des énergies de type quantique.
On a respectivement :
\[\begin{aligned} E_v&=a_v~A &&a_v~=~15,56~\rm MeV\\ E_s&=-a_s~A^{2/3} &&a_s~=~17,23~\rm MeV\\ E_c&=-a_c~\frac{Z(Z-1)}{A^{1/3}} &&a_c=0,7~\rm MeV\\ Z_a&=-a_a~\frac{(A-2Z)^2}{A} &&a_a~=~23,6~\rm MeV\\ E_p&=\pm a_p~A^{-1/2} &&a_p~=~11,2~\rm MeV\end{aligned}\]
Les différents termes sont en accord avec le fait que le noyau est supposé sphérique. Il est compact (volume proportionnel au nombre de nucléons), ce qui fait que son rayon est proportionnel à \(A^{\frac{1}{3}}\) (\(R~=~r_0~A^{1/3}\)).
5.2. Caractéristiques des énergies composantes
5.2.1. Énergie de volume \(E_v\)
Par analogie avec un gaz parfait de la thermodynamique, l’énergie interne est proportionnelle au nombre de particules qui composent ce gaz. On a donc : \[E_v=a_v~A\]
5.2.2. Énergie de surface \(E_s\)
Par analogie avec le phénomène de la tension superficielle d’une goutte liquide, intuitivement, les nucléons à la surface du noyau sont en contact avec un nombre de nucléons moins importants que ceux du centre.
D’autre part, compte tenu de l’expression de \(R\) notée précédemment : \[E_s=-a_s~A^{2/3}\]
5.2.3. Énergie de répulsion électrostatique
Les protons se repoussent mutuellement, d’où une diminution d’énergie de liaison.
On admet que le noyau est sphérique avec une densité de charge uniforme, D’où l’expression de l’énergie potentielle de cette distribution de charges : \[E=\frac{3}{5}~\frac{1}{4\pi~\varepsilon_0}~\frac{Q^2}{R}\]
-
\(Q\) : charge totale identifiable à \(Z~e\)
-
\(R\) : rayon de la sphère tel que \(R=r_0~A^{1/3}\)
La répulsion n’existe que lorsqu’il y a plus d’un proton, ce qui induit : \[Z^2~\rightarrow~Z~(Z-1)\]
Tous calculs faits : \[E_c=-\frac{3~e^2}{20\pi~\varepsilon_0~r_0}~\frac{Z~(Z-1)}{A^{1/3}}=-a_c~\frac{Z~(Z-1)}{A^{1/3}}\]
5.2.4. Énergie d’asymétrie
Dans la stabilisation du noyau, l’interaction forte doit contrebalancer l’effet de la répulsion électrostatique. De ce fait, les noyaux lourds ont besoin d’un excès de neutrons, d’où une asymétrie au détriment du nombre de protons.
C’est à ce moment qu’intervient l’effet quantique : l’excès de neutrons va contribuer parallèlement à augmenter l’énergie des nucléons sur leurs niveaux d’énergie. D’où cet effet sur l’énergie de liaison : \[E_a=-a_a~\frac{(N-Z)^2}{A}~=~a_a~\frac{(A-2~Z)^2}{A}\]
5.2.5. Énergie d’appariement
Les nucléons de spin demi-entier ont tendance à s’associer deux à deux de façon à se grouper en nombre pair. Un nombre impair de neutrons (ou de protons) sera ainsi moins stable.
Une formule empirique permet de rendre compte de cet effet en ajoutant à l’énergie de liaison \(E_p\) dite d’appariement (ou de parité) : \[E_p~=~a_p \left\{ \begin{aligned} &+A^{-1/2} &&\text{cas pair-pair~:~A pair, Z pair, N pair}\\ &~ &&\text{cas pair-impair~:~A impair, Z et N parités différentes}\\ &-A^{-1/2} &&\text{cas impair-impair~:~A pair, Z impair, N impair} \end{aligned} \right.\]
5.3. Exploitation de la formule \(B~W\)
Pour un nombre de masse donné \(A\), l’expression \(B~W\) est une forme quadratique en \(Z\) : \[B_A(Z)=(-a_c~A^{-1/3}-4~a_a~A^{-1})~Z^2+(a_c~A^{-1/3}+4~a_a)~Z+(a_v-a_a)~A-a_s~A^{2/3}\pm a_p~A^{-1/2}\]
Pour les noyaux stables, cette énergie de liaison est maximale. Il suffira de résoudre l’équation : \[\frac{\partial B_A(Z)}{\partial Z}~=~0\]
Le calcul conduit à : \[Z_{stab}\approx\frac{A}{2}~\frac{1+\cfrac{a_c}{4~a_a}~A^{-1/3}}{1+\cfrac{a_c}{4~a_a}~A^{-1/3}}\approx\frac{1}{2}~\frac{A}{1+\cfrac{a_c}{4~a_a}A^{2/3}}\]
6. Bilan des forces agissantes
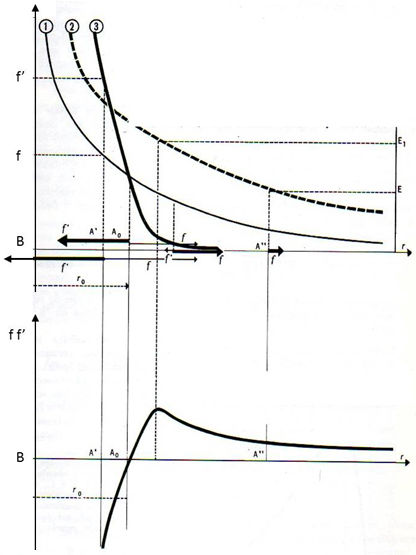 Le réseau de courbes ci-contre donne une bonne idée des interactions des forces en présence.
Le réseau de courbes ci-contre donne une bonne idée des interactions des forces en présence.
-
Courbe indiquant la valeur de la force répulsive de Coulomb \(\overrightarrow{f}\) en fonction de la distance \(r\) de deux particules ;
-
Courbe indiquant la valeur de la force attractive nucléaire \(\overrightarrow{f'}\) en fonction de \(r\) ;
-
Courbe indiquant l’énergie qu’il faut dépenser pour amener la particule \(A\) depuis une position très éloignée jusqu’à une distance \(r\) de la particule \(B'\).
La courbe de synthèse des actions indique la différence des deux forces coulombienne et nucléaire.
7. Note
L’eau lourde est donc un oxyde de deutérium \(D_2O\), que l’on peut encore écrire \(~_1^2H_2O\).
On retrouve dans l’eau lourde les mêmes éléments chimiques que dans l’eau ordinaire, mais les atomes d’hydrogène sont des isotopes lourds.
En poursuivant le processus, donc avec le tritium, on obtiendrait une eau super-lourde
Il peut être intéressant de comparer les propriétés physiques des deux types de produits : températures de congélation, températures d’ébullition, masse volumique. \[\begin{matrix} &\text{Propriétés physiques}&\text{Légère}~(H_2O)&\text{Lourde}~(D_2O)\\ & &------&------\\ &\text{Congélation} &0,00~^o\rm C &3,81~^o\rm C\\ &\text{Ébullition} &99,995~^o\rm C &101,42~^o\rm C\\ &\text{Masse volumique} &0,9982 &1,156 \end{matrix}\]
L’eau lourde est beaucoup plus dense que l’eau ordinaire, d’où son nom.
Elle est utilisée dans certains réacteurs nucléaires comme modérateur de neutrons. Elle permet de ralentir les neutrons issus de la réaction de fission nucléaire. Ces neutrons ralentis ont alors une probabilité plus élevée d’aller provoquer d’autres fissions des noyaux d’uranium, d’où la réaction en chaîne (indispensable à la réalisation de la pile atomique).
Certains se souviendront peut-être du film La bataille de l’eau lourde (film franco-norvégien tourné en 1948, donc peu après la seconde guerre mondiale). Ce film relate l’histoire vraie de la mission de sabotage (1943) contre une usine qui distillait de l’eau lourde pour l’Allemagne nazie en Norvège occupée. La première partie du film est centrée sur les recherches en physique nucléaire de l’équipe de Frédéric Joliot-Curie au Collège de France. D’ailleurs, le savant joue son propre rôle dans le film.

