1. Pression de radiation
L’émission d’ondes par une surface, de même que l’arrivée des ondes sur un obstacle, entraîne l’apparition d’effets mécaniques du second ordre connus sous le nom de pression de radiation, ou mieux de tension de radiation.
1.1. Pression axiale
Nous considérons un élément de tuyau sonore, de longueur \(l\) au repos, à parois indéformables, limité à gauche par un piston animé d’un mouvement oscillatoire et qui émet dans le tuyau des ondes sonores se dirigeant vers la droite. Ces ondes sont intégralement absorbées par un second piston situé à droite et qui oppose aux vibrations du fluide une résistance exactement égale à la résistance acoustique (impédance itérative).
Il s’agit par exemple d’un piston sans inertie, maintenu en position par un ressort de très grande longueur (l’effort constant équilibrant la pression moyenne du fluide) et dont le mouvement est amorti par un frottement visqueux exactement égal à la résistance acoustique.
Nous supposons que le mouvement de la tranche de fluide d’abscisse \(x\) au repos est exactement sinusoïdal et de la forme (y est le déplacement à partir du repos) : \[y=a~\cos\omega~(t-x/c)\]
En particulier, le mouvement des pistons émetteur et récepteur est : \[y_0=a~\cos\omega~t\quad;\quad y_1=a~\cos\omega~(t-l/c)\]
Supposons par exemple que \(l\) soit égale à un nombre entier de longueurs d’ondes, c’est-à-dire \(l=n~\cfrac{2\pi~c}{\omega}\), il en résulte que la distance des deux pistons au cours du mouvement reste constamment égale à leur distance au repos, soit \(l\).
L’expression de la dilatation du fluide est : \[\theta=\frac{\partial y}{\partial x}=\frac{a~\omega}{c}~\sin\omega~(t-x/c)\]
En première approximation, la surpression du fluide est en tout point égale à \(\theta/\chi\) . Poussons à la seconde approximation en tenant compte des termes du second ordre.
Nous écrirons alors, en désignant par \(v\) le volume spécifique du fluide, par \(\rho\) sa masse spécifique (\(\rho~v=cte\)) et en remarquant que le coefficient de compressibilité est lié à la célérité des ondes par :
\[\begin{aligned} c^2&=\frac{1}{\chi\rho}\quad\Rightarrow\quad\rho~c^2=-v~\frac{\partial p}{\partial v}\\ \delta p&=\frac{\partial p}{\partial v}~dv+\frac{\partial^2p}{\partial v^2}~\frac{(dv)^2}{2}=-\rho~c^2\theta+v^2~\frac{\partial^2p}{\partial v^2}~\frac{\theta^2}{2}\end{aligned}\]
Or : \[v\frac{d}{dv}(\rho~c^2)=-v~\frac{\partial v}{\partial p}-v^2~\frac{\partial^2v}{\partial p^2}\]
D’où : \[v^2~\frac{\partial^2v}{\partial p^2}=\rho~c^2~\Big(1-\frac{d(\rho~c^2)/\rho~c^2}{dv/v}\Big)\]
Comme : \[\frac{d(\rho~c^2)}{\rho~c^2}=\frac{d\rho}{\rho}+2~\frac{dc}{c}=-\frac{dv}{v}+2~\frac{dc}{c}\]
Il vient : \[v^2~\frac{\partial^2p}{\partial v^2}=2~\rho~c^2~\Big(1-\frac{v}{c}~\frac{dc}{dv}\Big)\]
Soit en définitive au 3° ordre près : \[\delta p=-\rho~c^2~\theta+\rho~c^2~\theta^2~\Big(1-\frac{v}{c}~\frac{dc}{dv}\Big)\]
\(\delta p\) comporte donc, outre un terme oscillant (du 1° ordre) à la pulsation \(\omega\), un terme du 2° ordre oscillant à la pulsation \(2~\omega\) et un terme constant et un terme constant que nous calculerons en remarquant que la valeur moyenne de \(\delta p\) est donnée par : \[\overline{\delta p}=\rho~c^2~\overline{\theta^2}~\Big(1-\frac{v}{c}~\frac{dc}{dv}\Big)=\frac{\rho~a^2~\omega^2}{2}~\Big(1-\frac{v}{c}~\frac{dc}{dv}\Big)\]
Remarquons alors que \(\rho~a^2~\omega^2/2\) représente la densité moyenne d’énergie vibratoire dans le fluide traversé par l’onde progressive, soit : \[E=2~E_c=2~\rho~\overline{\frac{u^2}{2}}=2~\rho~\frac{a^2~\omega^2}{2}\]
Il apparaît dès lors dans le fluide, du fait de l’établissement du mouvement oscillatoire, une surpression moyenne qui s’exprime en fonction de la densité d’énergie \(E\) sous la forme : \[\overline{\delta p}=E~\Big(1-\frac{v}{c}~\frac{dc}{dv}\Big)\]
Cette pression s’exerce notamment sur les pistons terminaux (émetteur et récepteur). Le maintien de ces pistons à une position moyenne identique à leur position de repos exige donc de la part de l’opérateur un effort supplémentaire destiné à équilibrer la pression de radiation \(\overline{\delta p}\).
1.2. Pression latérale
La pression moyenne de chaque tranche du fluide est également supérieure d’une quantité égale à \(\overline{\delta p}\) à sa pression au repos. Est-ce à dire que la pression moyenne sur les parois latérales du tuyau sonore est, elle aussi, élevée de \(\overline{\delta p}\) par la présence des ondes ? La réponse est non comme nous allons le voir en calculant la surpression moyenne sur un élément fixe de la paroi latérale d’abscisse \(x\).
Cet élément fixe ne suit pas, en effet, le mouvement du fluide. Lorsque le fluide est au repos, mais en cours d’oscillation, il est en contact avec la tranche de fluide dont l’abscisse au repos est \(x-y\) et c’est cette tranche de fluide qui exerce sur lui sa surpression \(\delta p(x-y,~t)\). Tout revient donc à calculer la valeur moyenne \(\delta p(x-y)\) en négligeant les termes du 3° ordre. Il vient : \[\overline{\delta p(x-y)}=\overline{\delta p(x,~t)}-\overline{y~\frac{\partial(\delta p)}{\partial x}(x,~t)}\]
Le premier terme du second membre est égal à : \(E~\Big(1-\cfrac{v}{c}~\cfrac{dc}{dv}\Big)\).
Dans le calcul du second, nous négligerons les termes du 2° ordre de \(\partial(\delta p)/\partial x\) qui conduiraient à des termes du 3° ordre après multiplication par \(y\). Nous écrirons donc : \[\frac{\partial(\delta p)}{\partial x}=-\frac{1}{\chi}~\frac{\partial\theta}{\partial x}=-\frac{1}{\chi}~\frac{\partial^2y}{\partial x^2}\]
Tout revient donc à calculer la valeur moyenne de la quantité : \[y~\frac{\partial^2y}{\partial x^2}=-\frac{a^2~\omega^2}{c^2}~\cos^2\omega~(t-x/c)\]
Cette valeur moyenne est manifestement égale à \(-\cfrac{a^2~\omega^2}{c^2}\). Le second terme de l’expression de \(\overline{\delta p(x-y)}\) s’écrit donc : \[-\Big\{-\frac{1}{\chi}~\Big(-\frac{a^2~\omega^2}{2~c^2}\Big)\Big\}=-\rho~\frac{a^2~\omega^2}{2}=-E\]
La surpression moyenne en tout point des faces latérales du tuyau est donc : \[\overline{\delta p(x-y)}=\overline{\delta p'}=-E~\frac{v}{c}~\frac{dc}{dv}\]
En définitive, l’action des ondes sur les parois de l’enceinte qui les renferme peut se décrire de la façon suivante :
a) Une surpression isotrope apparaît dans tout le fluide, de valeur : \[\delta p_{is}=-E~\frac{v}{c}~\frac{dc}{dv}\]
b) Une tension de radiation apparaît en outre sur les faces recevant normalement (ou émettant) les ondes. C’est elle qui constitue la véritable pression de radiation \(\delta p_{rad}\) dont l’expression est simple puisqu’elle s’identifie à la densité d’énergie des ondes.
1.3. Surpression isotrope
Il sera commode de vérifier expérimentalement la valeur de la tension de radiation. Il sera par contre difficile de mettre en évidence la surpression isotrope.
Nous avons en effet considéré jusqu’ici le cas où le fluide (supposons, par exemple, qu’il s’agit d’un liquide très peu compressible) est enfermé dans une enceinte de volume invariable (cas où la longueur est exactement égale à un nombre entier de longueurs d’onde) ou tout au moins dont le volume garde au cours des oscillations une valeur moyenne exactement égale à sa valeur au repos (cas d’une longueur quelconque).
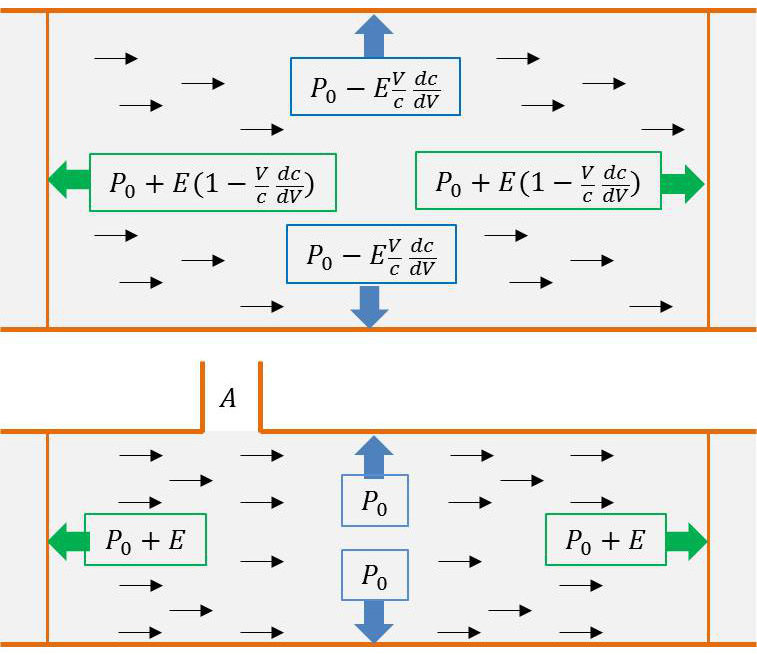 Nous sommes donc dans le cas de la première figure (voir ci-contre). Les surpressions exercées par le fluide sur les parois sont indiquées.
Nous sommes donc dans le cas de la première figure (voir ci-contre). Les surpressions exercées par le fluide sur les parois sont indiquées.
Ces surpressions sont toutefois difficiles à mesurer, car le moindre déplacement de la position moyenne des pistons entraîne une variation importante de la pression de repos \(P_0\) qui vient masquer les effets dus aux tensions de radiation.
Il vaut évidemment mieux imposer la pression de repos \(P_0\) en ménageant sur les parois latérales une ouverture à l’air libre \(A\) qui règle automatiquement à 1 atmosphère la pression de repos \(P_0\).
Supposons alors que nous établissions les ondes : une surpression isotrope tend à apparaître, mais elle se trouve immédiatement compensée par une légère dilatation du fluide qui montre très légèrement dans l’ajustage \(A\).
Il en résulte une annulation pratiquement complète (on peut négliger la hauteur dont le fluide monte dans l’ajustage) de la partie isotrope de la surpression due aux ondes (il s’agit de la valeur moyenne de la surpression et non de sa partie oscillante qui n’est que très légèrement perturbée si l’ajustage est étroit).
La pression sur les parois latérales est alors égale à \(P_0\) et elle devient \(P_0+E\) sur les faces terminales.
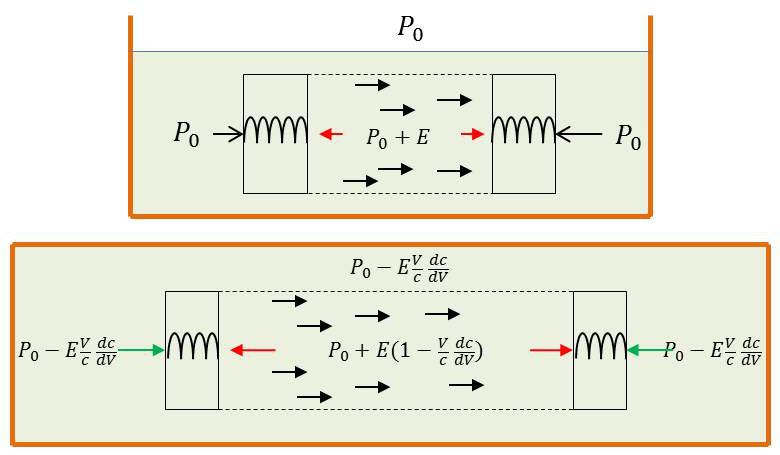 Un phénomène analogue se produit si un faisceau ultrasonore est produit au sein d’un liquide et absorbé à une certaine distance.
Un phénomène analogue se produit si un faisceau ultrasonore est produit au sein d’un liquide et absorbé à une certaine distance.
La pression de la partie du fluide qui reste au repos est égalisée avec la pression exercée sur ses faces latérales par le cylindre de fluide oscillant.
Si le récipient est ouvert à l’air libre, l’égalisation se produit par une légère chute de pression du fluide oscillant : \[-E~\frac{v}{c}~\frac{dc}{dv}~>~0\]
L’égalisation se produit par une légère compression du fluide au repos qui se transmet en tout point de ce fluide et notamment derrière la palette immergée.
Dans tous les cas l’effet global sur la palette immergée se réduit à l’action de la tension de radiation E.
Remarque
Nous avons supposé le mouvement du fluide exactement sinusoïdal en tout point et en avons déduit une expression de la surpression exacte au 3° ordre près. Toutefois, cette expression de la surpression, associée à l’expression du déplacement de chaque tranche de fluide, ne satisfait pas en toute rigueur l’équation de propagation des ondes dans le fluide.
En fait, elle n’y satisfait qu’au 2° ordre près, le terme oscillant du \(2^o\) ordre et de pulsation \(2~\omega\) qui figure dans \(\partial(\delta p/\partial x)\) ne pouvant être équilibré par un terme d’accélération en \(\partial^2y/\partial t^2\).
Il en résulte que le mouvement oscillatoire des tranches de fluide s’écarte progressivement, quand on s’éloigne de la source, d’un mouvement purement sinusoïdal (il apparaît progressivement une oscillation de fréquence double et même des termes de fréquences \(3~\nu,~4~\nu,~etc\). L’onde tend vers une structure d’équilibre qui n’est pas sinusoïdale.
Ceci n’est pas gênant si la longueur \(l\) n’est pas grande et si l’on a soin de considérer des ondes absorbées à l’abscisse \(l\).
Par contre, l’hypothèse d’une oscillation d’ensemble rigoureusement sinusoïdale ne pourrait plus se justifier dans le cas d’ondes stationnaires où de multiples réflexions allongent indéfiniment le trajet des ondes (en fait le phénomène d’absorption limitant ce trajet).
Revenons au cas d’un piston absorbant équivalent à la résistance acoustique du tuyau. En l’absence de dispersion (variation de la célérité avec la fréquence), l’absorption est totale pour toutes les composantes sinusoïdales et la pression de radiation exercée sur le piston par une onde de forme quelconque, sinusoïdale ou non, est numériquement égale à la densité moyenne d’énergie vibratoire.
Le fait que l’émetteur et le récepteur subissent la même action de la part des ondes (on suppose toujours qu’ils sont perpendiculaires à la direction de propagation des ondes) nous montre alors qu’il en est de même lorsque chacun des pistons peut être considéré à la fois comme émetteur et comme récepteur, ce qui est le cas lorsque nous établissons entre les deux pistons un régime d’ondes stationnaires.
Là encore, la pression de radiation exercée par le fluide sur les faces recevant normalement les ondes est numériquement égale à la densité moyenne d’énergie vibratoire dans le milieu soumis aux vibrations (cette densité moyenne est évidemment double de celle qui correspondrait pour l’un des pistons à l’onde incidente seule).
Exemple
Considérons un faisceau d’ondes ultra sonores excité par un quartz dans un liquide (eau par exemple) et qui vient se réfléchir à peu près totalement à la surface libre (la résistivité acoustique de l’air est bien plus faible que celle de l’eau).
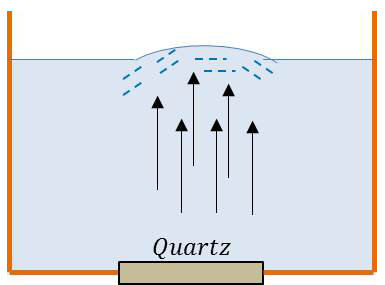 La pression atmosphérique extérieure ne peut équilibrer la pression de radiation qui est numériquement égale au double de la densité vibratoire se propageant vers le haut.
La pression atmosphérique extérieure ne peut équilibrer la pression de radiation qui est numériquement égale au double de la densité vibratoire se propageant vers le haut.
Le niveau libre de l’eau se soulève à la verticale du quartz comme si un violent courant liquide était injecté par le bas.
Le liquide monte d’ailleurs dans la colonne par suite du gradient de pression de radiation dû à l’absorption de l’onde.
Supposons que l’intensité de l’onde émise par le quartz et qui vient se réfléchir à la surface de l’eau soit : \[I=10~\rm W~cm^{-2}=10^5~W~m^{-2}\]
La densité d’énergie dans le fluide est : \[\frac{2~I}{c}=\frac{2\times10^5}{1450}=140~\rm J~m^{-3}\]
La pression de radiation (140 Pa =14 \(\times10^{-4}\) atm.) soulève localement la surface libre de l’eau d’une hauteur de 14 mm environ.
2. Ondes tombant sur une surface parfaitement réfléchissante
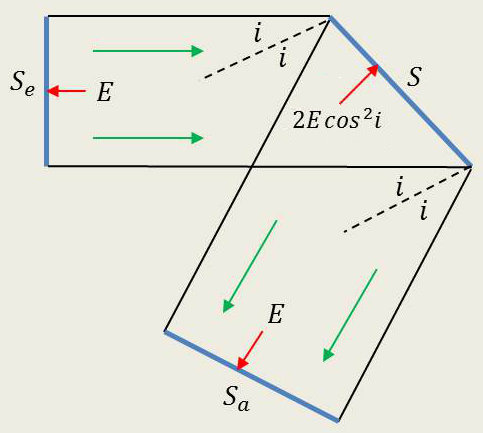 Considérons le montage ci-contre. Des ondes ultra sonores émises par une surface \(S_e\) sont réfléchies par une surface \(S\) qu’elles atteignent sous l’incidence \(i\) puis sont absorbées par une surface \(S_a\) normale à leur direction de propagation. On a : \[S_e=S_a=S~\cos~i\]
Considérons le montage ci-contre. Des ondes ultra sonores émises par une surface \(S_e\) sont réfléchies par une surface \(S\) qu’elles atteignent sous l’incidence \(i\) puis sont absorbées par une surface \(S_a\) normale à leur direction de propagation. On a : \[S_e=S_a=S~\cos~i\]
Lions entre elles les trois surfaces par une armature rigide placée à l’extérieur du fluide. L’ensemble est soumis de la part du fluide à un effort dont la résultante générale est nulle.
On peut s’en convaincre en faisant subir à l’ensemble un déplacement quelconque qui n’apporte au bilan énergétique aucune modification.
Soit \(E\) la densité moyenne d’énergie au voisinage de \(S_e\). La même densité d’énergie se retrouve au voisinage de \(S_a\).
L’équilibre d’ensemble exige que la surface \(S\) soit soumise de la part du fluide à une force qui équilibre la somme vectorielle des efforts reçus par \(S_e\) et \(S_a\), soit : \[\overrightarrow{F}=-(\overrightarrow{F_e}+\overrightarrow{F_a})\]
On voit immédiatement que \(\overrightarrow{F}\) est orientée suivant la normale à \(S\) (dirigée vers le fluide au repos) et que sa grandeur est : \[E~S_e~\cos i+E~S_a~\cos i=2~E~S~\cos^2 i\]
La surface \(S\) est donc soumise à un effort normal par unité de surface \(2~E~\cos^2i\), c’est-à-dire à un effort égal au produit par de la densité moyenne d’énergie au voisinage de la surface réfléchissante \(S\).
3. Ondes tombant sur une surface partiellement réfléchissante
Reprenons à présent les calculs dans le cas d’une surface \(S\) partiellement réfléchissante. Désignons par \(R\) le facteur de réflexion et considérons deux cas distincts :
3.1. Premier cas : surface partiellement absorbante
La fraction de l’énergie transmise \((1-R)\) est absorbée dans l’épaisseur de la surface S dont la face opposée est au repos et ne transmet pas de vibration au fluide.
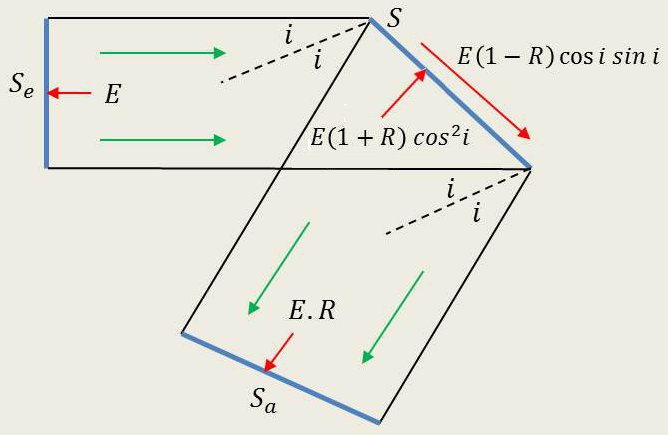 Le raisonnement précédent peut alors être repris, l’ensemble solidaire \(S_e,~S_a,~S\) n’étant soumis à aucun effort extérieur de la part du fluide.
Le raisonnement précédent peut alors être repris, l’ensemble solidaire \(S_e,~S_a,~S\) n’étant soumis à aucun effort extérieur de la part du fluide.
La force \(F\) équilibre la somme géométrique des efforts qui s’exercent sur \(S_e\) et \(S_a\) :
-
au voisinage de \(S_e\) la densité d’énergie est \(E\) ;
-
au voisinage de \(Sa\) la densité d(énergie est \(E~R\).
\(F\) a donc suivant la normale à \(S\) une composante normale : \[E~(S_e+R~S_a)~\cos i=E~(1-R)~\cos^2 i\]
et comporte en outre une composante tangentielle (dans le plan de la figure) : \[E~(S_e-R~S_a)~\sin i=E~(1-R)~\cos i~\sin i\]
Soit un effort normal sur \(S\) par unité de surface : \[E~(1+R)~\cos^2 i\]
et un effort tangentiel par unité de surface : \[E~(1-R)~\sin i~\cos i\]
Remarquons que l’effort normal reste égal au produit par \(\cos^2i\) de la densité d’énergie au voisinage de \(S\).
3.2. Second cas : surface oscillante
La fraction de l’énergie transmise \((1-R)\) traverse \(S\) et continue sur sa face opposée.
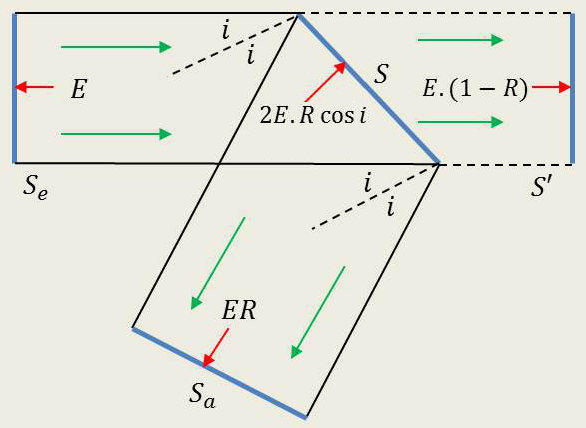 Nous sommes ramenés au cas précédent en disposant à la suite de \(S\), normalement au faisceau incident, une surface parfaitement absorbante \(S'\).
Nous sommes ramenés au cas précédent en disposant à la suite de \(S\), normalement au faisceau incident, une surface parfaitement absorbante \(S'\).
C’est alors l’ensemble \(S+S'\) qui est soumis aux efforts équilibrant les efforts exercés sur \(S_e\) et \(S_a\).
Or, l’effort reçu par \(S'\) est : \[E~(1-R)~\cos~i\]
Puisque : \[S'=S~\cos~i\]
il devient égal à : \[2~E~S~R~\cos^2i\]
soit un effort normal par unité de surface : \[2~E~R~\cos^2i\]
L’effort tangentiel sur \(S\) se trouve réduit de : \[E~S'~(1-R)~\sin~i\]
et disparaît par suite complètement (voir la figure).
Tout se passe en définitive comme si l’énergie sonore était acheminée par des corpuscules transportant une quantité de mouvement égale au quotient de leur énergie par la célérité de l’onde.
Ceci est très général et se retrouve identiquement dans le cas des vibrations lumineuses.
Remarques
Dans le dernier cas que nous avons considéré, on peut interpréter les résultats en considérant qu’à l’effort normal exercé sur \(S\) par le fluide situé du côté de l’émetteur, soit à \(E~(1+R)~\cos^2i\) par unité de surface, se retranche l’effort normal exercé par les vibrations transmises de l’autre côté de \(S\), soit \(E~(1-R)~\cos^2i\).
De la même façon, on vérifierait que les efforts tangentiels s’annulent exactement.
4. Transfert d’ondes entre deux fluides différents
Considérons maintenant le cas où la surface \(S\) constitue la surface de séparation de deux fluides différents non miscibles. Restreignons-nous à l’incidence normale et supposons en outre que les résistivités acoustiques soient les mêmes, de sorte qu’il n’y a pas d’onde réfléchie.
L’intensité transmise est égale à l’intensité incidente, mais les densités d’énergie sont différentes des deux côtés de \(S\) et un effort s’exerce sur \(S\).
Si \(I\) est l’intensité incidente, les densités d’énergie devant \(S\) et derrière \(S\) sont respectivement \(I/c\) et \(I/c'\) et \(S\) reçoit un effort normal : \[I~\Big(\frac{1}{c}-\frac{1}{c'}\Big)\]
qui est dirigée en sens inverse de la direction de propagation des ondes si \(c'<c\) (rappelons que nous avons admis que \(\rho~c=\rho'~c'\)).
Cet effet s’interprèterait aisément dans la conception corpusculaire ; les corpuscules voient leur quantité de mouvement accrue à la traversée de \(S\) (leur nombre et leur énergie totale se conservant), d’où une répulsion vers l’arrière de la surface \(S\).
5. Invariant adiabatique
Entre deux pistons plongés dans un liquide, établissons un système d’ondes stationnaires, qui comporte nécessairement un nombre entier \(n\) de nœuds de vitesse (n pouvant être nul, évidemment) en plus de deux nœuds situés sur les pistons, dont la distance est \(l\).
Rapprochons très lentement les deux pistons (c’est-à-dire de façon que la quantité dont ils se rapprochent pendant une période de vibration soit très petite devant la longueur d’onde). Lorsque les deux pistons se sont rapprochés de \(l\), le nouvel état vibratoire au sein du fluide est nécessairement représenté par une onde stationnaire comportant le même nombre de nœuds.
Il est en effet impossible que la modification infiniment petite apportée à l’état du système par le rapprochement de \(l\) des deux pistons entraîne une modification macroscopique de son état vibratoire telle par exemple que l’apparition d’un nœud supplémentaire.
Continuons à rapprocher les deux pistons. Nous arriverons à modifier notablement la longueur de la colonne de fluide en vibration qui passe à la longueur \(l'\), sans que le nombre de nœuds de vitesse ait changé. Il existe donc entre la longueur \(l\) et la longueur d’onde des vibrations la relation : \[\frac{1}{\lambda}=\text{cte}=\frac{n-1}{2}\]
Ce que nous pouvons écrire en introduisant la fréquence \(\nu\) des vibrations et en remarquant que \(\lambda=c/\nu\) soit \(\lambda\nu=\text{cte}\) donc \(\nu l=\text{cte}\) ou, sous forme différentielle : \[\frac{dl}{l}+\frac{dv}{v}=0\]
Remarquons alors que le rapprochement des deux pistons a nécessité de la part de l’opérateur la production d’un travail qui a, en définitive, été complètement utilisé à élever l’énergie vibratoire.
Or : \[dW=-E~S~dl=-2~E_c~S~dl\]
soit, en désignant par \(\mathcal{E}_c\) l’énergie cinétique totale du système en vibration : \[\mathcal{E}_c=V~E_c=S~l~E_c\]
et en remarquant que \(dW\), accroissement total d’énergie vibratoire, est égal à \(2~d\mathcal{E}_c\) : \[d\mathcal{E}_c=\frac{\mathcal{E}_c~S~dl}{V}\quad\Rightarrow\quad\frac{d\mathcal{E}_c}{\mathcal{E}_c}=-\frac{dl}{l}=\frac{d\nu}{\nu}\]
D’où la relation : \[\frac{d\mathcal{E}_c}{\nu}=\text{cte}\]
La quantité \(\mathcal{E}_c/\nu\), invariante lors d’une modification très lente des conditions extérieures imposées à l’oscillateur constitué par la colonne de fluide, porte le nom d’invariant adiabatique(le mot adiabatique signifie ici qu’aucune modification rapide, source de vibrations de période comparable à celle de l’oscillateur, n’est imposée au fluide).
Dans le cas où les oscillateurs sont constitués par des molécules, s’abstenir de leur conférer des modifications de fréquence comparable à leur fréquence propre revient à s’abstenir de leur fournir de la chaleur, d’où le terme de modification adiabatique.
Ehrenfest a étendu à l’ensemble des systèmes périodiques la relation ci-dessus, qui s’applique notamment (théorème de l’invariant adiabatique d’Ehrenfest) aux systèmes quantifiés atomiques soumis à une lente variation des conditions extérieures qui leur sont imposées. La conséquence est qu’une modification adiabatique très lente ne modifie que les niveaux d’énergie du système quantifié sans modifier les degrés d’occupation de ses divers niveaux et laisse par suite l’entropie du système inchangé.
Revenons à notre cylindre de fluide oscillant, et cherchons par quel mécanisme se modifie la fréquence lors d’une variation de longueur. La modification a lieu par effet Doppler ainsi que nous allons le voir dans l’article suivant.

