1. Notion de travail adiabatique

On considère un système séparé du milieu extérieur par une enceinte adiabatique, c’est-à-dire imperméable à la chaleur. On suppose que cette enceinte peut être traversée par des passages de courant, par des tiges rotatives, etc. et qu’elle peut être éventuellement déformée pour permettre des échanges de travail du système avec le milieu extérieur.

Un échange de travail qui s’effectue dans ces conditions sera désigné sous le nom d’échange de travail adiabatique.

Nous convenons comme toujours de compter positivement le travail adiabatique lorsqu’il est reçu par le système.

Nous désignons sous le nom de transformations adiabatiques les transformations que peut subir, dans ces conditions, le système. Nous ne nous restreignons nullement aux transformations réversibles, ni quasi statiques ; le système pourra se trouver hors d’équilibre pendant la transformation.

Insistons sur ce point que nous englobons dans le système tout ce qui se trouve à l’intérieur de l’enceinte adiabatique (par exemple une résistance électrique). Tout ce qui se trouve hors de l’enceinte adiabatique fait partie du milieu extérieur.

Considérons alors une transformation adiabatique faisant passer le système de l’état d’équilibre initial \(I\), caractérisé par les variables thermodynamiques \([x_i~,~y_i,~\dots]\) à l’état d’équilibre \(F\) caractérisé par les variables \([x_f~,~y_f,~\dots]\).

Nous pouvons mesurer, à l’aide des modifications du milieu extérieur, le travail qu’a reçu le système pendant cette transformation adiabatique.

Ce travail est désigné par :

\[\begin{aligned} &W_{ad}\\ I&\rightarrow F\end{aligned}\]

2. Premier principe de la thermodynamique

Il existe une infinité de transformations adiabatiques distinctes pouvant amener le système d’un état initial bien déterminé à un état final également bien déterminé. On peut même imaginer des transformations violentes dès l’instant ou seuls les équilibres de l’état initial et de l’état final sont toujours les mêmes. Le travail reçu est toujours le même.

Nous considérons ce résultat comme absolument général et formulerons ainsi le premier principe de la thermodynamique :

Lorsqu’un système quelconque passe d’un état initial déterminé à un état final déterminé par voie uniquement adiabatique, le travail total qu’il reçoit du milieu extérieur est toujours le même, quel que soit le chemin adiabatique qu’il a suivi entre ces deux états.

3. Énergie interne

Il résulte du premier principe que le travail adiabatique que fournit un système donné en passant de l’état d’équilibre initial \(I\) à l’état d’équilibre final \(F\) dépend uniquement de ces deux états \(I\) et \(F\).

Nous pouvons donc écrire : \[\begin{aligned} &W_{ad}\\ I&\rightarrow F \end{aligned} ~~~ =~\varphi(I,F) =~\varphi(x_i,~y_i,~\dots,~x_f,~y_f,~\dots)\]

La fonction \(\varphi\) dépend évidemment du système considéré.

Choisissons arbitrairement, et définitivement, un état d’équilibre \(O\) du système et supposons que l’on puisse passer par voie adiabatique de cet état \(O\) à l’état \(I\) ou \(F\).

Dans le sens \(O \rightarrow I\), le système reçoit le travail : \[\begin{aligned} &W_{ad}\\ O&\rightarrow I \end{aligned} ~ =~\varphi(O,I)\]

Dans le sens \(O \rightarrow F\), le système reçoit le travail : \[\begin{aligned} &W_{ad}\\ O&\rightarrow F \end{aligned} ~ =~\varphi(O,F)\]

Envisageons alors deux transformations qui amènent le système de l’état \(O\) à l’état \(F\) :

• la première est celle qui vient d’être indiquée ;

• la deuxième est composée des deux transformations successives \(O \rightarrow I\) et \(I \rightarrow F\) au cours desquelles le système reçoit le travail total :

\[\begin{aligned} &W_{ad}\\ O&\rightarrow I \end{aligned} ~+~ \begin{aligned} &W_{ad}\\ I&\rightarrow F \end{aligned}\]

D’après le premier principe, le travail adiabatique est le même dans ces deux transformations. On a donc : \[\begin{aligned} &W_{ad}\\ O&\rightarrow F \end{aligned} = \begin{aligned} &W_{ad}\\ O&\rightarrow I \end{aligned} + \begin{aligned} &W_{ad}\\ I&\rightarrow F \end{aligned}\]

C’est-à-dire : \[\varphi(O,F)=\varphi(O,I)+\varphi(I,F)\]

En définitive : \[\begin{aligned} &W_{ad}\\ I&\rightarrow F \end{aligned} = \varphi(I,F) =\varphi(O,F)-\varphi(O,I)\]

Mais l’état \(O\) est un état standard que nous pouvons considérer comme origine pour les états du système et dont les coordonnées sont des constantes.

Une fois choisi cet état d’origine, la quantité \(\varphi(O,F)\) ne dépend que de l’état \(F\) ; de même que la quantité \(\varphi(O,I)\) ne dépend que de l’état \(I\).

Nous pouvons donc exprimer le travail adiabatique \(W_ad\) reçu par le système dans la transformation \(I \rightarrow F\) par : \[\begin{aligned} &W_{ad}\\ I&\rightarrow F \end{aligned} = U(F)-U(I)\]

Et nous pouvons alors énoncer le résultat suivant :

Le travail reçu par un système déterminé dans une transformation adiabatique quelconque est égal à la différence des valeurs que prend pour l’état final et l’état initial. C’est une certaine fonction des coordonnées thermodynamiques du système désignée sous le nom d’énergie interne.

Remarquons que nous avons utilisé pour l’introduire un état d’origine arbitraire et que, par suite, l’énergie interne est ainsi définie à une constante additive près.

Fournir du travail adiabatique à un système revient donc à accroître son énergie interne d’une quantité égale au travail adiabatique qu’il reçoit. Ceci est en parfait accord avec la notion de conservation de l’énergie.

Un système qui fournit au milieu extérieur un travail adiabatique donné, subit une diminution d’énergie interne exactement égale. De même qu’un ressort qui fournit le travail \(W\) en se détendant subit une diminution d’énergie potentielle égale à \(W\).

Remarque

La fonction \(U\) n’est définie qu’à une constante additive près. Seule pourra être déterminée expérimentalement la différence d’énergie interne entre deux états \(A\) et \(B\) : \[U_A-U_B=U(x_A,~y_A,~\dots)-U(x_B,~y_B,~\dots)\]

Pour mesurer cette différence, il faut, en principe, trouver un chemin adiabatique conduisant de \(B\) à \(A\).

Nous verrons que, s’il n’est pas possible de réaliser une transformation adiabatique \(A \rightarrow B\), il est certainement possible de la réaliser de \(B \rightarrow A\).

La variation d’énergie interne peut toujours être déterminée dans un sens ou dans l’autre : \[U_A-U_B = \begin{aligned} &W_{ad}\\ B&\rightarrow A \end{aligned} =~-~ \begin{aligned} &W_{ad}\\ A&\rightarrow B \end{aligned}\]

L’énergie interne est une fonction de l’état du système que nous supposons être un état d’équilibre pour pouvoir le décrire au moyen de coordonnées thermodynamiques. Elle est donc fonction de toutes les coordonnées définissant cet état d’équilibre.

Il pourra arriver toutefois que certaines coordonnées ne soient pas nécessaires, le nombre de variables dont dépend \(U\) étant au maximum égal au nombre de variables indépendantes nécessaires pour décrire l’état du système.

Pour une certaine masse gazeuse par exemple, l’équation d’état réduit à deux le nombre de variables indépendantes.

\(U\) pourra donc être considérée comme une fonction \(U(p,~v)\) ou bien \(U(v,~T)\) ou bien \(U(p,~T)\).

Nous pourrons alors exprimer la variation d’énergie interne dans une transformation infinitésimale \(dp,~dv,~dT\) sous l’une ou l’autre des formes :

\[\begin{aligned} &dU=\Big(\frac{\partial U}{\partial p}\Big)_v~dp+\Big(\frac{\partial U}{\partial v}\Big)_p~dv\\ &dU=\Big(\frac{\partial U}{\partial v}\Big)_T~dv+\Big(\frac{\partial U}{\partial T}\Big)_v~dT\\ &dU=\Big(\frac{\partial U}{\partial p}\Big)_T~dp+\Big(\frac{\partial U}{\partial T}\Big)_p~dT\end{aligned}\]

4. Transformations non adiabatiques

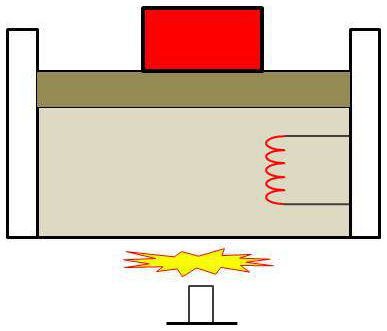Considérons le système formé d’une masse d’eau où se trouve plongée une résistance électrique enfermée dans une enceinte dont le fond est diatherme. Allumons un bec de gaz au-dessous.

Sans brancher de générateur sur la résistance, nous obtenons un résultat tout à fait analogue à celui que nous aurions obtenu en laissant éteint le bec de gaz et en faisant passer un courant dans le résistance.

Nous pouvons donc obtenir par des moyens non mécaniques (la combustion du gaz ne pouvant en aucune manière être ramenée à l’abaissement d’un poids dans le milieu extérieur) des effets analogues à ceux que produit l’absorption de travail par le système.

Nous allons maintenant préciser ces considérations en comparant les résultats obtenus dans les deux expériences.

Dans la première expérience, le système passe de l’état \(I\) à l’état \(F\) par voie adiabatique  : \[\begin{aligned} &W_{ad}\\ I&\rightarrow F \end{aligned} ~=~ U(f)-U(I)\]

Dans la deuxième, le système passe du même état initial \(I\) au même état final \(F\) mais par voie non adiabatique.

Au cours de son évolution, on a mis le système en communication avec le milieu extérieur (celui-ci n’est pas en général en équilibre thermique avec lui) par une cloison diatherme.

On aura donc :

\[\begin{aligned} &W\\ I&\rightarrow F \end{aligned} ~\neq~ \begin{aligned} &W_{ad}\\ I&\rightarrow F \end{aligned} \quad\Rightarrow\quad \begin{aligned} &W\\ I&\rightarrow F \end{aligned} ~\neq~ U(F)-U(I)\]

Or, le système a reçu dans la transformation une quantité d’énergie égale au second membre. Nous devons donc reconnaître qu’il a reçu du milieu extérieur de l’énergie par un autre moyen que celui qui consiste à lui fournir du travail.

Cette quantité d’énergie ainsi fournie au système par des moyens non mécaniques est évidemment égale à [\(U_F-U_I-W \)]. Nous la représentons par la lettre \(Q\) et la désignons sous le nom de chaleur.

Nous écrivons alors : \[Q=U_F-U_I-W\]

Et nous considérons cette équation comme l’expression mathématique du premier principe de la thermodynamique.

Remarque

Supposons qu’un système soit en équilibre thermodynamique avec le milieu extérieur. Les forces extérieures n’exercent sur lui aucun travail et nous l’amenons préalablement à l’équilibre thermique avec le milieu extérieur de température invariable \(T\), au moyen d’une cloison diatherme.

L’équilibre atteint, nous le renfermons dans une enceinte adiabatique, sa température reste \(T\) et toutes ses coordonnées thermodynamiques gardent des valeurs immuables.

Remettons le système en communication avec le milieu extérieur par une cloison diatherme et abstenons-nous de lui fournir du travail. Son état ne varie nullement puisqu’il est déjà en équilibre thermique avec le milieu extérieur. Son énergie interne ne varie donc pas et il ne reçoit aucun travail, ce qui veut dire qu’il ne reçoit aucune chaleur.

Renfermons le système dans sa cloison adiabatique et faisons passer à une valeur différente \(T'\) la température du milieu extérieur, sans exercer le moindre travail sur le système ; celui-ci reste en équilibre à la température \(T\).

Introduisons alors de nouveau la cloison diatherme et abstenons-nous toujours de fournir du travail au système ; l’équilibre est rompu et le système tend vers un nouvel état d’équilibre où sa température est \(T'\).

Son état change donc et il en est de même de son énergie interne puisqu’il ne reçoit pas de travail et qu’il reçoit cependant de l’énergie. Nous devons en conclure qu’il reçoit de la chaleur.

Nous remarquons que tout échange de chaleur du système et du milieu extérieur est lié :

• à l’existence d’une cloison diatherme mettant en communication le système et le milieu extérieur ;

• à l’existence d’une différence de température entre le système et le milieu extérieur (cette différence pouvant être infiniment petite mais non nulle).

Nous traduirons ceci en disant qu’une cloison diatherme est perméable à la chaleur ou encore qu’elle constitue un conducteur thermique et qu’elle ne peut transmettre de la chaleur qu’entre deux milieux à températures différentes.

Par contre, une cloison adiabatique est imperméable à la chaleur et constitue ainsi un isolant thermique.

Un concept particulier

Nous avons ainsi rejoint le concept courant d’échange de chaleur entre deux milieux à températures différentes tendant à égaliser leurs températures, avec cette différence importante que la chaleur n’apparaît pas comme une sorte de fluide mystérieux, mais simplement comme de l’énergie de transit.

Le transfert de chaleur à travers une cloison diatherme est donc un simple transfert d’énergie par une méthode ne nécessitant pas un échange de travail.

Une fois l’équilibre atteint entre les deux milieux séparés par une cloison diatherme, ce transfert d’énergie s’arrête ; la chaleur n’apparaît plus, seule garde un sens l’énergie interne de chacun des milieux.

5. Échanges de chaleur à l’intérieur d’une enceinte adiabatique

Considérons un système composite formé de deux parties \(A\) et \(A'\), séparément à l’équilibre et séparées par une cloison adiabatique.

L’ensemble \(AA'\) est entouré d’une enceinte adiabatique. L’énergie interne de \(A\) est \(U_i\) et celle de \(A'\) est \(U'_i\).

Introduisons entre \(A\) et \(A'\) une cloison diatherme et fournissons à l’ensemble \(AA'\) un travail \(W_0\). Laissons s’établir un nouvel équilibre où \(A\) et \(A'\) auront la même température.

Pendant l’opération :

• \(A\) aura fourni à \(A'\) un travail \(W\) ;

• \(A\) aura reçu du milieu extérieur un travail ;

• \(A'\) aura reçu du milieu extérieur un travail ;

• \(A\) aura reçu une chaleur \(Q\) ;

• \(A'\) aura reçu une chaleur \(Q'\).

Bilan de l’opération :

Appliquons le premier principe (énergie internes de \(A\) et \(A'\) dans l’état final \(U_F\) et \(U'_F\)).

L’ensemble \(AA'\) n’a reçu que du travail adiabatique. Son énergie interne \(U+U'\) a varié d’une quantité \(W_0=W_1+W_2\).

On a donc : \[(U_F+U'_F)-(U_I+U'_I)=W_1+W_2+Q+Q'=W_1+W_2\]

C’est à dire que  : \[Q+Q'=0\qquad\text{donc}\quad Q=-Q'\]

La chaleur reçue (ou cédée) par la partie \(A\) est égale à la chaleur cédée (ou reçue) par la partie \(A'\).

C’est là le principe de base de la calorimétrie, science qui a pour but l’étude des échanges de chaleur. L’ensemble des parties \(A\) et \(A'\) avec l’enceinte adiabatique qui les renferme est un calorimètre.

6. Unité calorimétrique de quantité de chaleur

L’égalité \(W+Q=U_F-U_I \) est une égalité entre grandeurs physiques de même nature, impliquant que la chaleur est de l’énergie en transit et a a priori la même unité que l’énergie mécanique. La quantité de chaleur \(Q\) y est donc exprimée en joules, au même titre que le travail ou la variation d’énergie interne.

Les physiciens ont cependant introduit une unité particulière appelée calorie.

Nous dirons qu’un système reçoit une quantité de \(N\) calories lorsqu’on peut considérer que cette chaleur lui est fournie par \(N\) grammes d’eau se refroidissant de 15,5 à 14,5 °C (à la pression atmosphérique normale), en n’échangeant de chaleur qu’avec le système. Ou l’opération inverse bien entendu.

On utilise parfois la grande calorie ou kilocalorie (1000 calories).

On démontre, si l’on veut exprimer \(Q\) en calorie qu’il faut écrire alors : \[W+J~Q=U_F-U_I\]

\(J\) est appelée équivalent mécanique de la calorie : \[J\approx 4,186~{\rm joules/calorie}\]