1. Généralités

Nous allons tenter de déduire les principes de la thermodynamique d’une étude microscopique où seront pris en considération les éléments constitutifs du système microscopique étudié.

Nous supposerons que les interactions entre les molécules sont négligeables mais non nulles, de telle sorte que des échanges d’énergie puissent lieu de l’une à l’autre, ce qui est la condition pour que l’assemblée des diverse molécules qui constituent le système thermodynamique puisse évoluer vers un équilibre d’ensemble.

2. Représentation microscopique d’une assemblée de molécules

Considérons une assemblée d’un très grand nombre N de molécules toutes identiques. L’état d"une molécule individuelle (position, orientation, mouvement d’ensemble, vibrations, etc.) peut être défini par un ensemble de coordonnées \(\{q,~p\}\) dites conjuguées.

En principe, les premières sont les coordonnées de position et les secondes les coordonnées d’impulsion. De la sorte, l’énergie de la molécule pourra être exprimée par une fonction \(U\) de l’ensemble de ses coordonnées : \[U(q_1,~q_2,~\dots,~q_r~;~p_1,~p_2,~\dots,~p_r)\]

Nous pouvons représenter l’état de cette molécule par un point dans l’espace des \(\{q,p\}\)  ; c’est une extension en phase à \(2~r\) dimensions.

Imaginons que l’on puisse partager cet espace en cellules extrêmement petites. Leur nombre C est naturellement beaucoup plus grand que le nombre total des molécules. La connaissance du degré d’occupation \(n_i\) de chacune des cellules définit ce que l’on appelle la complexion de l’assemblée.

Les cellules étant à priori arbitrairement petites (en réalité, la mécanique quantique leur impose un volume minimum), nous devons admettre que la connaissance de la complexion correspond au maximum d’information que nous pouvons théoriquement obtenir sur l’état physique de l’assemblée des N molécules.

Comme \(C \gg N\), on peut affirmer que la plupart des degrés d’occupation sont nuls. Ainsi, la probabilité pour que \(n_i>1\) est très faible et on peut admettre que \(\overline{n_i}\approx 0\). Ce qui conduit à adopter un autre découpage.

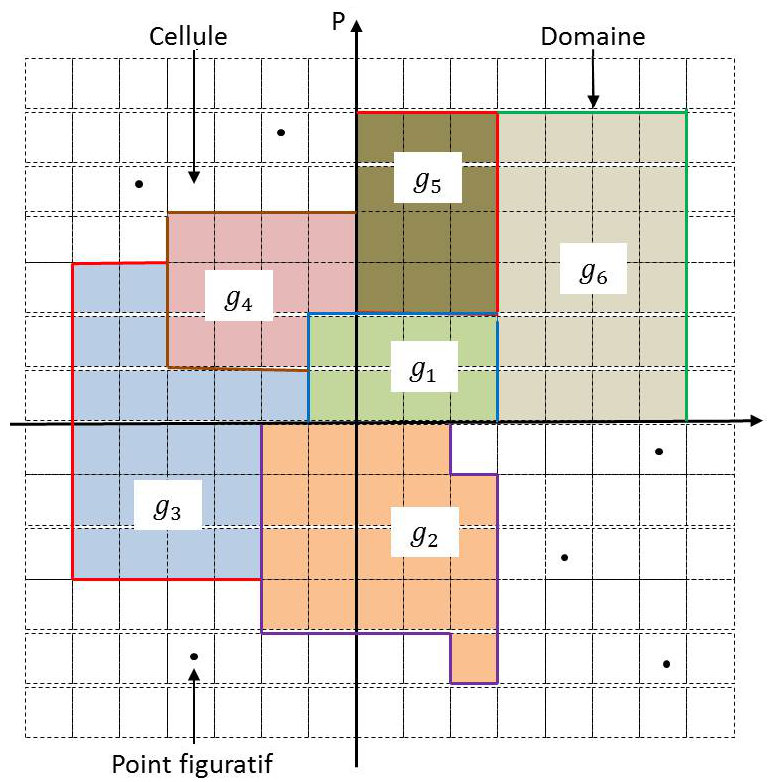L’extension est découpée en domaines (numérotés de 1 à D) et nous désignons par \(g_i\) le nombre de cellules adjacentes que comporte le i-ème domaine.

Le nombre de domaines est donc très inférieur à celui des molécules. Il en résulte que le nombre de point figuratifs dans un domaine déterminé est en général très grand et que sa valeur moyenne est donc très supérieure à l’unité.

Nous dirons que la connaissance du degré d’occupation \([N_i~;~\overline{N_i} \gg 1]\) de chacun des domaines définit l’état microscopique de l’assemblée de molécules.

En effectuant des calculs classiques d’analyse combinatoire, on démontre que le nombre de dispositions distinctes des \(N_i\) points figuratifs dans les cellules du i-ème domaine est (statistique de Maxwell–Boltzmann) : \[W_i=\frac{(N_i+g_i-1)!}{N_i~!~(g_i-1)!}\]

D’où le nombre de complexions qui conduisent à l’état microscopique \([N_1,~\dots,~N_i,~\dots,~N_D]\) : \[W=\prod_{i=1}^D W_i=\prod_{i=1}^D\frac{(N_i+g_i-1)!}{N_i!~(g_i-1)!}\]

Remarque

W mesure la probabilité de l’état mais comme ce nombre est très grand, il ne peut s’agir de probabilité au sens mathématique du terme sauf en lui substituant le rapport \(W/\sum W_i\). Nous pourrions d’ailleurs constater que W varie d’un état à l’autre dans des proportions gigantesques.

Une fois l’équilibre atteint, il ne faudrait pas croire que l’assemblée cesse d’évoluer et reste invariablement dans le même état (celui qui correspond au maximum de W).

En revanche, et si le nombre de molécules est assez grand, l’assemblée a la quasi-certitude, une fois l’équilibre atteint, de voir son état évoluer au voisinage immédiat de l’état pour lequel W est maximum. L’évolution de l’assemblée se réduit donc à de faibles fluctuations autour de cet état de probabilité maximum.

3. État d’équilibre d’une assemblée isolée

L’assemblée étant supposée isolée, son contenu total d’énergie est donc invariable. \(U_i\) étant l’énergie de toute molécule dont le point figuratif se trouve dans le i-ème domaine et \(N_i\) le nombre de telles molécules, l’énergie totale de l’assemblée est : \[U=\sum_{i=1}^D N_i~U_i=cte\qquad\text{avec}\quad~N=\sum_{i=1}^D=cte\]

Nous recherchons l’état pour lequel W doit être maximum ou encore mieux \(\ln(W)\). Cela revient à rechercher l’ensemble des \(N_i\) pour lequel un ensemble de petites variations laisse W stationnaire.

Pour cela deux relations doivent être satisfaites : \[(1)\qquad \left\{ \begin{aligned} N&=cte\quad\Rightarrow\quad\sum_{i=1}^D\delta N_i=0\\ U&=cte\quad\Rightarrow\quad\sum_{i=1}^D U_i~\delta N_i=0\\ \end{aligned} \right.\]

Ce qui entraîne : \[\delta\{\ln(W)\}=0\]

Il faut donc partir de la relation exprimant \(W\) avec \(\{N_i,~g_i\} \gg 1\) : \[\ln(W)=\sum_{i=1}^D \ln\{(n_i-g_i)!\}-\ln\{N_i!\}-\ln\{g_i!\}\]

En appliquant la formule de Stirling : \[\ln(n!)=n~\ln(n)-n\]

il vient : \[\ln(W)=\sum_{i=1}^D \big\{(N_i+g_i)~\ln(N_i+g_i)-N_i~\ln(N_i)-g_i~\ln(g_i) \big\}\]

Tous calculs faits : \[\delta\{\ln(W)\}=\sum_{i=1}^D \ln\Big\{\frac{N_i+g_i}{N_i}\Big\}~\delta N_i\]

Nous voulons donc avoir comme conséquence des relations (1) ci-dessus : \[\sum_{i=1}^D \ln\Big\{\frac{N_i+g_i}{N_i}\Big\}~\delta N_i=0\]

Le premier membre de l’équation doit être une combinaison linéaire des deux premiers membres des deux équations suivantes, c’est-à-dire : \[\ln\frac{N_i+g_i}{N_i}=\alpha+\beta~U_i\]

qui peut encore s’écrire \((g_i \gg N_i)\): \[{\overline{n}_i}=\frac{n_i}{g_i}=\exp\{-(\alpha+\beta~U_i)\}\]

\({\overline{n}}_i\) : degré d’occupation moyen des cellules du i-ème domaine.

Soit \(d\tau\) le volume des cellules élémentaires. Chaque cellule située du i-ème domaine contient en moyenne \(\overline{n_i}\) points figuratifs ; un élément de volume \([dv=dq_1\dots dq_i\dots dq_r\dots dp_1\dots dp_i\dots dp_r]\) entourant le point \([q_1,~\dots,~q_r,~\dots,~p_1,~\dots,~p_r]\) contient un nombre de points figuratifs : \[dn=\overline{n_i}~\frac{dv}{d\tau}=A~\exp\{-\beta U(q_1,..,p_r)\}~dq_1\dots dp_r \quad;\quad A=\Big\{\frac{\exp(-\alpha)}{d\tau}\Big\}\]

La constante est déterminée par la condition \(\iint\dots\iint dn=N\)

et en définitive : \[\frac{dn}{N}= \frac{\exp\{-\beta~U(q_1,~\dots,~p_r)\}~dq_1\dots dp_r}{\iint\dots\iint \exp\{-\beta~U(q_1,~\dots,~p_r)\}~dq_1\dots dp_r}\]

Les intégrales étant étendues à tout le domaine de variation des \(q\) et des \(p\). Cette expression représente la proportion des molécules dont le point figuratif se trouve dans l’élément \(d\tau\) entoure le point \([q_1,~\dots,~q_r,~p_1,~\dots,~p_r]\) de l’extension en phase, ou encore la probabilité qu’un des points figuratifs pris au hasard se trouve dans cet élément.

Appliquons ce résultat à un ensemble de \(N\) molécules monoatomiques non soumises à un champ de forces extérieures (en particulier nous négligeons l’influence de la pesanteur). Pour ces molécules, la seule forme d’énergie susceptible de se modifier est l’énergie cinétique de translation.

Nous définirons dès lors l’état d’une molécule par 6 coordonnées \(\{x,~y,~z,~v_x,~v_y,~v_z\}\).

Nous devrions en principe associer à \(x\) la quantité \(p_x=m~v_x\), etc., mais le choix des vitesses comme coordonnées d’impulsion ne change rien au raisonnement.

L’énergie totale de la molécule est : \[U_{totale}=U_0+m~\frac{v_x^2+v_y^2+v_z^2}{2}\]

Nous supposons les molécules sans interactions à distance (gaz parfait). Le terme \(U_0\) peut être négligé puisqu’il est invariable et qu’il disparaît donc dans l’expression \(dn/dN\).

La proportion des molécules pour lesquelles l’abscisse est comprise entre \(x\) et \(x + dx\), etc. et la vitesse \(v_x\) comprise entre \(u\) et \(u+du\), etc. est exprimée par : \[\frac{dn}{N}=\frac{\exp\{-\beta~m~(u^2+v^2+w^2)/2\}~dx~dy~dz~du~dv~dw} {\iiint\iiint\exp\{-\beta~m~(u^2+v^2+w^2)/2\}~dx~dy~dz~du~dv~dw}\]

La séparation en deux parties multiplicatives de l’intégrale figurant au dénominateur montre que l’on peut écrire (calcul élémentaire) : \[dn=\frac{N}{V}~dv\]

La concentration moléculaire est uniforme dans l’enceinte (hypothèse du chaos moléculaire maintenant démontrée).

Cherchons maintenant le nombre de molécules dont le point de vitesse est compris dans la cellule \(\{u,~u+du~;~v,~v+dv~;~w,~w+dw\}\) sans nous préoccuper de leur position dans l’enceinte. Nous aurons à intégrer \(dn\) sur l’ensemble des valeurs possibles de \(\{x,~y,~z\}\) ce qui fera apparaître \(V\) au numérateur alors qu’il se trouve déjà au dénominateur.

Il viendra donc : \[\frac{dn}{N}=N~\frac{\exp\{-\beta~m~(u^2+v^2+w^2)/2\}~du~dv~dw}{\iiint\exp\{-\beta~m~(u^2+v^2+w^2)/2\}~du~dv~dw}\]

L’intégration au dénominateur (calcul élémentaire) conduit à la valeur: \[\Big\{\frac{2\pi}{\beta~m}\Big\}^{3/2}\]

Et on retrouve ainsi la loi de distribution de Maxwell (\(\beta=1/k~T\)) : \[\frac{dn}{N}=\Big\{\frac{2\pi}{\beta~m}\Big\}^{3/2}~\exp\{-\beta~m~(u^2+v^2+w^2)/2\}~du~dv~dw\]

Ce résultat a été obtenu indépendamment de toute hypothèse initiale sur l’homogénéité de l’isotropie de la distribution des vitesses, hypothèses qui deviennent maintenant des théorèmes dans le cadre de la statistique classique que nous avons développée.

4. Équilibre d’ensemble de deux assemblées de molécules

Nous considérons maintenant deux assemblées A et B :

• la première \(N_A\) molécules A, toutes identiques ;

• la deuxième \(N_B\) molécules B, toutes identiques mais différentes des molécules A.

Les points représentatifs sont identifiés par les coordonnées \(\{(q_A,~p_A)~;~(q_B,~p_B)\}\). Les espaces des A et B sont partagés en cellules et domaines numérotés.

L’état d’ensemble du système \([A,~B]\) est représenté par la connaissance des nombres \(N_i^A\) des molécules A occupant le domaine \(i\) et \(N_j^B\) des molécules B occupant le domaine \(j\). De la sorte, le nombre total des complexions conduisant à un état déterminé de l’ensemble est : \[W=\prod_i\frac{(N_i^A+g_i^A-1)!}{N_i^A!~(g_i^A-1)!}\times\prod_j\frac{(N_j^B+g_j^B-1) !}{N_j^B!~(g_j^B-1)!}\]

Il faut tenir compte du fait que l’ensemble \([A,B]\) à l’équilibre a une énergie invariable.

Deux cas peuvent alors se présenter suivant la nature de la cloison entre les deux assemblées : cloison adiabatique et indéformable ou cloison diatherme.

4.1. Cloison adiabatique et indéformable entre les deux assemblées

L’énergie totale des molécules A reste alors constante de même que celles des molécules B. Les deux assemblées sont alors indépendantes et nous pouvons représenter pour chacune d’elles séparément les calculs du paragraphe précédent aboutissant à des répartitions :

\[\begin{aligned} &N_i^A=A~\exp(-\beta_A~U_i^A)\\ &N_j^B=B~\exp(-\beta_B~U_j^B)\end{aligned}\]

Tout l’état d’équilibre des \(A\) peut être ainsi associé à tout état d’équilibre des \(B\) pour donner un état d’équilibre de l’ensemble.

4.2. Cloison diatherme entre les deux assemblées

Dans ce cas, des échanges d’énergie sont possibles entre les deux assemblées. La seule condition qui subsiste est alors que l’énergie totale de l’ensemble \([A,~B]\) reste constante.

Nous serons amenés à postuler que, pour tout ensemble de variations \(\{\delta n_i^A,~\delta n_j^B\}\), on doit avoir : \[\left\{ \begin{aligned} &\sum_i\delta n_i^A=0\\ &\sum_j\delta n_j^B=0\\ &\sum_iU_i^A~\delta n_i^A+\sum_jU_j^B~\delta n_j^B=0 \end{aligned} \right.\]

On constatera que cette fois les deux termes de la dernière relation ne sont pas séparément nuls.

Nous devrons avoir automatiquement : \[\sum_i \ln\frac{N_i^A+g_i^A}{N_i^A}~\delta N_i^A+\sum_j \ln\frac{N_j^B+g_j^B}{N_j^B}~\delta N_j^B=0\]

Pour que cette dernière équation soit conséquence des trois précédentes, il faut que son premier membre soit une combinaison linéaire des premiers membres de ces trois équations ; il faut pour cela qu’il existe trois constantes \(\alpha_A\), \(\alpha_B\) et \(\beta\) telles que :

\[\begin{aligned} &\sum_i \ln\frac{N_i^A+g_i^A}{N_i^A}~\delta N_i^A+\sum_j \ln\frac{N_j^B+g_j^B}{N_j^B}~\delta N_j^B\\ \approxeq\\ &\alpha_A\sum_i\delta n_i^A+\alpha_B\sum_j\delta n_j^B+\beta~\Big\{\sum_i U_i^A~\delta N_i^A+\sum_j U_j^B~\delta N_j^B\Big\}\end{aligned}\]

Le signe choisi indique que l’égalité doit être vérifiée pour un ensemble de \(\delta N_i^A\) et \(\delta N_j^B\) absolument arbitraires. Ceci exige que les coefficients des \(\delta N_i^A\) et \(\delta N_j^B\) soient les mêmes dans les deux membres, soit, avec le même \(\beta\) dans les deux équations :

\[\begin{aligned} &\ln\frac{N_i^A+g_i^A}{N_i^A}=\alpha_A+\beta~U_i^A\\ &\ln\frac{N_j^B+g_j^B}{N_j^B}=\alpha_B+\beta~U_j^B\end{aligned}\]

En supposant que : \[g_i^A~ \gg ~N_i^A\quad;\quad~g_j^B~ \gg ~N_j^B\]

et en posant : \[A=\exp(-\alpha_A)\quad;\quad~B=\exp(-\alpha_B)\]

on peut écrire, toujours avec le même \(\beta\) dans les deux équations :

\[\begin{aligned} &\frac{N_i^A}{g_i^A}=\overline{N_i^A}=A~\exp(-\beta~U_i^A)\\ &\frac{N_j^B}{g_j^B}=\overline{N_j^B}=B~\exp(-\beta~U_j^B)\end{aligned}\]

La présence de la cloison diatherme exige donc l’égalité des deux coefficients \(\beta\) dans les deux distributions. Ce qui revient à dire que le coefficient \(\beta\) peut être considéré comme une mesure de la température commune aux deux assemblées séparées par la cloison diatherme.

Il suffit alors de considérer que les molécules B sont des molécules d’un gaz parfait monoatomique pour identifier \(\beta\) avec l’expression \(1/k~T\), et trouver la relation entre l’échelle de température que constituent les \(\beta\) (que nous pourrions appeler échelle statistique et introduite logiquement par la mécanique statistique) et l’échelle absolue des T.

D’où ce résultat très important :

Dans une assemblée de N molécules A en équilibre à la température T, le nombre de molécules dont le point figuratif est contenu dans la cellule \[\{(q_1,~q_1+dq_1)\dots(q_r,~q_r+dq_r)~;~(p_1,~p_1+dp_1)\dots(p_r,~p_r+dp_r)\]

de l’extension en phase, cellule à laquelle correspond une énergie pour une molécule, est : \[dn=A~\exp\{\frac{-U(q_1,~\dots,~p_r)}{k~T}\}~dq_1~\dots~dp_r\]

A est une constante que l’on peut déterminer par : \[A~\iint\dots\iint\exp\{\frac{-U~(q_1,~\dots,~p_r)}{k~T}\}~dq_1~\dots~dp_r=N\]

5. Équipartition de l’énergie

Considérons un ensemble de formes d’énergies en supposant que les paramètres de position (centre de gravité) sont \(\{x,~y,~z\}\) et les paramètres de vitesse sont \(\{v_x,~v_y,~v_z\}\).

On aura donc :

– Énergie cinétique de translation : \[E_c^{tr}=m~(v_x^2+v_y^2+v_z^2)\]

– Énergie cinétique de rotation : \[E_c^{rot}=\frac{1}{2}~I_{\theta}~{\dot{\theta}}^2\]

Le mouvement de vibration supposé sinusoïdal le long d’un axe de la molécule : \[\mu~\frac{d^2\xi}{dt^2}+K~\xi=0\]

induit deux autres types d’énergie :

– Énergie potentielle d’oscillation : \[E_p^{osc}=\frac{1}{2}~K~{\xi}^2\]

– Énergie potentielle d’oscillation : \[E_c^{osc}=\frac{1}{2}~\mu~{\dot{\xi}}^2\]

On peut encore adjoindre deux autres types d’énergie potentielle :

– Une fonction des coordonnées \(\Phi(x,~y,~z)\) si la molécule est soumise à un champ de forces dérivant d’un potentiel (attraction terrestre par exemple).

– Une fonction de coordonnées généralisées \(U'(q_1,~q_2,~\dots,~q_n)\)

La somme de ces énergies faisant apparaître tous les paramètres conduisent à une expression de la forme : \[U(x,~y,~z~;~v_x,~v_y,~v_z~;~\dot{\theta}~;~\xi,~\dot{\xi}~;~q_1,~\dots,~q_n)\]

Et pour exprimer le nombre de molécules dont le point figuratif est dans la cellule \((x,~x+dx)\), etc. : \[dn=A~\exp\Big\{-\frac{1}{k~T}\Big\}~\sum \{\text{énergies}\}~dx~dy~dz~\dots~dq_j~\dots~dq_n\]

Calcul dans un cas particulier

Cherchons par ailleurs le nombre \(dn\) de molécules pour lesquelles l’une des coordonnées par exemple \(\xi\) est comprise dans l’intervalle \([\xi,~\xi+d\xi]\), les autres ayant des valeurs quelconques.

Nous obtiendrons ce nombre \(dn\) en intégrant l’expression précédente sur le domaine de variation de toutes les coordonnées autres que \(\xi\).

Posons : \[U=U_0+\frac{1}{2}~K~{\xi}^2\]

On a alors : \[dn=n(\xi)~d\xi=A~\exp\Big\{\frac{-K\xi^2}{2k~T}\Big\}~d\xi\int \dots \int\exp\Big\{-\frac{U_0}{k~T}\Big\}~dx~dy~\dots~dq_n\]

L’intégrale, ne dépendant pas de \(\xi\), étant notée B : \[dn=A~B~\exp\Big\{\frac{-K~\xi^2}{2k~T}\Big\}~d\xi\]

Le produit A B est défini par : \[N=\int dn=A~B~\int_{-\infty}^{+\infty}\exp\Big\{-\frac{K~\xi^2}{2k~T}\Big\}~d\xi\]

Il vient en définitive : \[dn=N\frac{\exp\{-K~\xi^2/2k~T]}{\int_{-\infty}^{+\infty}\exp\{-K~\xi^2/2k~T\}}~d\xi\]

Cherchons la moyenne de \(\xi^2\) \[\overline{\xi^2}=\frac{\int_{-\infty}^{+\infty}\xi^2~n(\xi)~d\xi}{\int_{-\infty}^{+\infty}n(\xi)~d\xi}\]

C’est-à-dire : \[\overline{\xi^2}=\frac{\int_{-\infty}^{+\infty}\exp\{-K~\xi^2/2k~T\}~\xi^2~d\xi} {\int_{-\infty}^{+\infty}\exp\{-K~\xi^2/2k~T\}~d\xi}\]

On intègre par parties le numérateur en posant : \[u=\xi\quad;\quad dv=\exp\{-K~\xi^2/2k~T\}~\xi~d\xi\]

L’intégrale du dénominateur apparaît en facteur et le calcul se simplifie, d’où : \[\overline{\xi^2}=\frac{k~T}{K}\]

On obtient une forme encore plus remarquable avec l’écriture équivalente : \[\overline{\Big\{-\frac{K~\xi^2}{2}\Big\}}=\frac{k~T}{2}\]

Elle fait apparaître l’énergie potentielle moyenne d’oscillation des molécules à la température T le long de cet axe.

Nous aurions le même résultat pour toutes les formes d’énergie pouvant s’exprimer par une relation du type \(E=\lambda~q^2\), c’est-à-dire notamment pour l’énergie cinétique de translation suivant les trois axes, l’énergie cinétique de rotation suivant un axe quelconque, l’énergie potentielle et l’énergie cinétique correspondant à toutes les vibrations.

Nous avons ainsi démontré sous forme d’un théorème l’équipartition de l’énergie entre les divers degrés de liberté et les diverses formes d’énergie.

Nous savons déjà que ces calculs ne sont valables que pour les degrés de liberté auxquels correspond une énergie effectivement susceptible de s’échanger dans les chocs. Cette restriction n’apparaît pas dans la statistique que nous avons développée, du fait qu’elle est classique et ignore les restrictions imposées par la mécanique quantique.

Remarque

En toute rigueur, il faudrait remarquer que le calcul que nous avons fait suppose constants les coefficients des carrés des coordonnées dans l’expression de l’énergie. Ceci est vrai par exemple pour l’énergie cinétique de translation \((m~v^2_x/2\) suivant une direction, mais n’est plus vrai, en toute rigueur pour l’énergie cinétique de rotation d’une molécule alors diatomique, dans laquelle \(I_\theta\) dépend de \(\xi\), degré d’allongement de la molécule lors de la vibration des atomes le long de la ligne joignant leur centre de gravité.

Les variables \(\xi\) et \(\dot{\theta}\) ne se séparent alors pas complètement dans l’intégration, ce qui semble introduire une difficulté, mais on peut aisément la lever en triant parmi les molécules celles qui ont une extension \(\xi\) donnée, c’est-à-dire un moment d’inertie \(I_{\theta}\in[I,~I+dI]\).

Il n’y a plus à intégrer sur \(\xi\) et l’on trouve une valeur moyenne : \[\overline{\Big\{\frac{I_{\theta}~\dot{\theta}^2}{2}\Big\}}=\frac{k~T}{2}\qquad\text{pour}\quad I\leq I_{\theta}\leq I+dI\]

Cette valeur moyenne est toujours la même quel que soit l’intervalle choisi et la valeur moyenne de l’énergie cinétique de rotation pour l’ensemble des molécules, quel que soit leur degré d’extension à l’instant considéré et par suite la valeur instantanée de leur moment d’inertie est bien égale à \(k~T/2\).

Cette façon de procéder revient en somme à considérer momentanément comme des molécules différentes celles dont le degré d’extension est différent. Ces molécules vues comme différentes se mettent toutes à l’équilibre thermique à la même température T et prennent par suite la même énergie cinétique moyenne de rotation.

6. Distribution spatiale des molécules dans un champ de forces

Considérons à présent le terme d’énergie potentielle \(\Phi(x,~y,~z)\) apporté par un champ de forces extérieur agissant sur les molécules. Ce terme va introduire une différence de concentration moléculaire d’un point à l’autre de l’enceinte.

En effet, cherchons le nombre de molécules situées dans le petit élément de volume entourant le point \((x,~y,~z)\) où l’énergie potentielle est \(\Phi(x,~y,~z)\).

En intégrant sur toutes les coordonnées autres que \((x,~y,~z)\), nous obtenons : \[dn=C~\exp\Big\{-\frac{\Phi(x,~y,~z)}{k~T}\Big\}~dx~dy~dz=c(x,~y,~z)~dv\]

\(c(x,~y,~z)\) : concentration moléculaire au voisinage du point \((x,~y,~z)\).

Déterminons le nombre de molécules situées dans un élément de volume \(dv\) entourant un point \((x_0,~y_0,~z_0)\) où l’énergie potentielle des molécules est \(\Phi(x_0~,y_0,~z_0)\)  : \[dn=C~\exp\Big\{-\frac{\Phi(x_0,~y_0,~z_0)}{k~T}\Big\}~dV=c(x_0,~y_0,~z_0)~dv\]

Nous obtenons le résultat suivant :

Si la différence d’énergie potentielle, due au champ de forces extérieures, entre les deux points \((x,~y,~z)\) et \((x_0,~y_0,~z_0)\) est \(\Phi-\Phi_0\), le rapport des concentrations est donné par la relation : \[\frac{c(x,~y,~z)}{c(x_0,~y_0,~z_0)}=\exp\Big\{-\frac{\Phi-\Phi_0}{k~T}\Big\}\]

Application

L’énergie potentielle d’une molécule dans le champ de pesanteur est \(W=m~g~z\).

Supposons alors l’atmosphère terrestre à température uniforme \(T\) (il sera prudent de se limiter à de petits domaines).

Le rapport des concentrations moléculaires en deux points d’altitude \(z\) et \(z_0\) est : \[\frac{c(z)}{c(z_0)}=\exp\Big\{-\frac{m~g~(z-z_0)}{k~T}\Big\}\]

D’où la pression au point d’altitude \(z\) (\(T\) y étant constante) : \[P=P_0~\exp\Big\{-\frac{m~g}{k~T}\Big\}\]

\(P_0\) : pression au niveau de la mer \((z = 0)\).

Ce résultat aurait pu être obtenu par des considérations plus élémentaires. La formule générale qui a été démontrée s’applique aussi par exemple à la sédimentation de particules solides très petites dans un liquide.

L’étude expérimentale de la sédimentation de particules de résine a permis à Jean Perrin, par application de la formule de Boltzmann, d’obtenir une des premières mesures expérimentales du nombre d’Avogadro \(N=R/k\).