1. Introduction et rappels

Nous désignons sous le nom de système chimique un ensemble de substances chimiques en équilibre qui ne peut recevoir de travail que des forces de pression extérieures .

Le système a une pression, un volume et une température bien déterminée, dans chacun de ses états d’équilibre. Si nous avons fait le choix d’un état origine pour le calcul des énergies internes, le premier principe nous apprend qu’à chaque état correspond une énergie interne bien déterminée.

Dans une transformation quelconque : $$\Delta U=U_F-U_I=W+Q$$

Dans une transformation à volume constant, la chaleur totale reçue par le système est égale à sa variation d’énergie interne.

En effet, $W=0$ puisque $V$ n’a pas varié.

Dans une transformation à pression extérieure constante faisant passer le système d’un état d’équilibre initial à un état d’équilibre final, la chaleur totale reçue par le système est égale à sa variation d’enthalpie. En effet, la pression du système dans les états d’équilibre $I$ et $F$ est $P$, égale à la pression extérieure constante.

Dans les états intermédiaires, qui ne sont pas obligatoirement des états d’équilibre, la pression peut n’être pas définie, mais peu importe. On écrit que : $$U_F-U_I=W+Q$$

La pression extérieure étant constamment égale à $P$, nous aurons, en désignant par $V_I$ et $V_F$ les volumes initial et final : $$W=P~(V_I-V_F)=(P~V_I)-(P~V_F)$$

Soit : $$Q=U_F-U_I+(P~V-F)-(P~V_I)=H_F-H_I$$

On a donc bien : $$Q=\Delta H$$

2. Application aux réactions chimiques

Soit la réaction chimique entre les corps $\{A_1,~\dots,~A_m\}$ conduisant aux corps $\{A'_1,~\dots,~A'_m\}$ représentée par la relation : $$\sum_i \nu_i~A_i\quad\rightarrow\quad\sum_j \nu_j~A'_j+Q~(\text{chaleur dégagée})$$

Le système dans l’état initial sera l’ensemble des $\nu_1$ moles du corps $A_1$, ..., $\nu_m$ moles du corps $A_m$ prises isolément à la température T. Son énergie interne est $U_I$.

On met en contact les corps, la réaction s’effectue et l’on obtient l’état final des corps. La température ayant été maintenue constante par un thermostat. L’énergie finale est $U_F$.

2.1. Réaction à volume constant

Une réaction à volume constant, par exemple à l’intérieur d’une bombe, dégage une chaleur $Q_V$ (chaleur de réaction à volume constant). On a : $$Q_V=U_I-U_F=-\Delta U \quad (\text{chaleur dégagée})$$

2.2. Réaction à pression constante

La chaleur dégagée par une réaction à pression constante est $Q_P$ (chaleur de réaction à pression constante), la plus couramment utilisée, car les réactions chimiques ont lieu en général à la pression atmosphérique. $$Q_P=H_I-H_F=-\Delta H$$

Remarquons que l’état final n’est pas le même (en général) que dans l’expérience à volume constant.

3. Variation de la chaleur de réaction avec la température

Nous choisissons le cas d’une réaction à pression constante, le plus usuel. À la température $T$, on aura : $$\Big\{\sum_i \nu_i~A_i\Big\}_T \quad \rightarrow \quad \Big\{\sum_j \nu_j~A'_j\Big\}_T+Q_P(T)$$

À la température $T+dT$ : $$\Big\{\sum_i \nu_i~A_i\Big\}_{T+dT} \quad \rightarrow \quad \Big\{\sum_j \nu_j~A'_j\Big\}_{T+dT}+Q_P(T+dT)$$

Les deux réactions ont lieu à la même pression.

Désignons par $C_{PI}$ la capacité calorifique moléculaire à pression constante du corps $A_i$, par $C_{PJ}$ celle du corps $A'_j$.

Envisageons la transformation globale à pression constante : $$\Big\{\sum_i \nu_i~A_i\Big\}_{T+dT}~~\rightarrow~~\Big\{\sum_i \nu_i~A_i\Big\}_{T}~~\rightarrow~~\Big\{\sum_j \nu_j~A'_j\Big\}_{T}~~\rightarrow~~\Big\{\sum_j \nu_j~A'_j\Big\}_{T+dT}$$

La variation totale d’enthalpie du système dans cette transformation est : $$\Delta H=\sum_i \nu_i~C_{pi}~\{(-dT)+(-Q~dT)\}+\sum_j \nu_j~C'_{pj}~dT$$

C’est la même dans la réaction directe à la température $T + dT$, c’est-à-dire : $$\Delta H=-Q_p(T+dT)$$

On en tire :

$$\begin{aligned} Q_p(T+dT)-Q_p(T)&=\sum_i \nu_i~C_{pi}~dT-\sum_j \nu_j~C'_{pj}~dT\\ \Rightarrow\qquad \frac{dQ_p}{dT}&=\sum_i \nu_i~C_{pi}-\sum_j \nu_j~C'_{pj}\end{aligned}$$

On trouverait de même pour une réaction à volume constant : $$\frac{dQ_v}{dT}=\sum_i \nu_i~C_{vi}-\sum_j \nu_j~C'_{vj}$$

Les $C_{vi},~C'_{vi}$ représentant les capacités calorifiques moléculaires à volume constant. Insistons bien sur le fait que $Q$ représente ici la chaleur dégagée par la réaction, c’est-à-dire la chaleur de réaction au sens couramment adopté en chimie.

4. Chaleur latente de vaporisation

Nous considérons la transformation faisant passer un gramme de fluide à la température constante $T$ de l’état initial liquide de saturation à l’état final vapeur saturante.

Premier cas

La transformation est conduite de façon réversible, à la pression constante $P$ (pression de vapeur saturante). Le point figuratif dans le diagramme de Clapeyron décrit la palier de vaporisation $AA'$.

Nous désignerons sous le nom de chaleur latente de vaporisation la chaleur reçue pendant cette transformation, soit $L$.

Calculons la variation d’énergie interne du fluide :

– Travail reçu : $$W=-p~(u'-u)$$

– Variation d’énergie interne : $$\Delta U=U_{A'}-U_A=L-p(u'-u)$$

Deuxième cas

La transformation est conduite sans travail extérieur. Ce sera le cas si le fluide est constamment enfermé dans une enceinte de volume invariable. Ceci peut sembler difficile à réaliser ; il suffira cependant de le placer dans une enceinte indéformable (diatherme) de volume intérieur $u'$, ampoule renfermant le liquide de saturation, l’enceinte étant parfaitement vidée de tout gaz et de briser cette ampoule.

La vaporisation est alors évidemment irréversible ; dans l’état final, l’enceinte est emplie de vapeur saturante. La chaleur totale absorbée par le système pendant cette transformation à travail extérieur nul est alors : $$L_i=U_{A'}-U_A=L-p~(u'-u)$$

On la désigne couramment sous le nom de chaleur interne de vaporisation.

4.1. Variation avec T de la chaleur latente de vaporisation

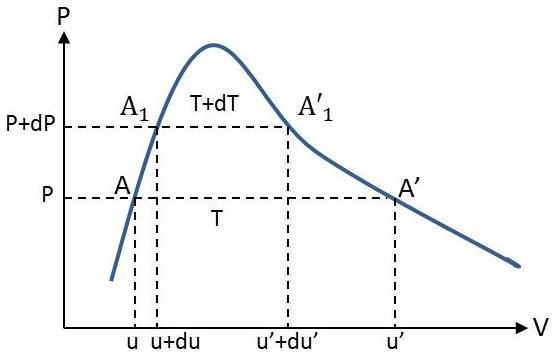
Nous considérons les deux paliers de vaporisation infiniment voisins (température $T$, pression $p$) et (température $T + dT$, pression $p + dp$).

La transformation $AA'$ peut être conduite, soit directement par le palier $A'$, soit par l’intermédiaire de la série de transformations suivantes (se reporter au graphique précédent) :

• $AA_1$ : transformation infinitésimale où le fluide reste constamment à l’état liquide, à l’extérieur de la courbe de saturation ;

• $A_1A'_1$ : palier ;

• $A'_1A'$ : transformation dans laquelle le fluide reste constamment à l’état de vapeur, à l’extérieur de la courbe de saturation.

Écrivons que : $$U_{A'}-U_A=(U_{A'}-U_{A'_1})+(U_{A'_1}-U_{A_1})+(U_{A_1}-U_A)$$

Avec :

$$\begin{aligned} &U_{A'}-U_A=L-p~(u'-u)\\ &U_{A'}-U_{A'_1}=C'_p~(-dT)+h'~(-dp)-p~(-du')\end{aligned}$$

$C'_p~,~h'$ désignent les coefficients calorimétriques relatifs à la vapeur sèche.

Soit : $$U_{A'}-U_{A'_1}=-C'_p~dT-h'~dp+p~du'$$

De même : $$U_{A_1}-U_A=C_p~dT+h~dp+p~du$$

$C_p~,~h$ désignent les coefficients calorimétriques relatifs au liquide.

En outre : $$U_{A'_1}-U_{A_1}=L+dL-(p+dp)$$

relation dans laquelle $(L + dL)$ désigne la chaleur latente de vaporisation à la température $(T + dT)$.

Il vient alors :

$$\begin{aligned} L-p~(u'-u)=&L+dL-(p+dp)~(u'-u+du'-du)\\ &+(C_p-C'_p)~dT+(h-h')~dp+p~(du'-du)\end{aligned}$$

En négligeant le terme du second ordre : $$dL=(C'_p-C_p)~dT+(u'-u+h'-h)$$

Le volume spécifique $u$ du liquide de saturation est petit si $T \gg T_c$ et par suite négligeable.

De même, $h$ est très petit, car : $$h=-\frac{(C_p-C_v)}{(\partial p/\partial T)_v}$$

et le dénominateur est très grand pour un liquide dont la compressibilité est très faible (rappelons que $T \gg T_c$).

Nous négligerons donc $h$ et $u$.

En outre, assimilons la vapeur à un gaz parfait, ce qui est justifiable loin du point critique.

On a alors : $$h'=u'$$

Et il reste : $$dL=(C'_p-C_p)~dT\quad\Rightarrow\quad\frac{dL}{dT}=C'_p-Cp$$

D’où l’on tirera : $$L=L_0+\int_{T_0}^T (C'_p-C_p)~dT$$