1. Entropie et désordre

Imaginons un cristal de \(NaCl\) (ions \(Na^+\) et \(Cl^-\) en réseau tridimensionnel), lancé à une vitesse \(V\) au sein d’une enceinte adiabatique. Le cristal vient s’arrêter sur l’une des parois : on observe que sa température s’est un peu élevée.

D’un point de vue macroscopique, nous traduirons ce fait en remarquant que son énergie cinétique de translation s’est convertie en énergie interne, d’où accroissement de cette dernière qui se traduit par une élévation de température ; ceci est conforme au premier principe.

Ce principe ne s’opposerait pas à ce que la transformation inverse se produise, le cristal repartant à la vitesse \(V\) au prix d’un abaissement de température le ramenant à son état initial ; mais le second principe s’y oppose, cette seconde transformation étant la transformation exactement inverse d’une transformation réelle. Il ne donne toutefois pas la raison de cette évidente impossibilité.

Passons à l’étude microscopique du phénomène. La température du cristal est liée à l’agitation thermique des ions \(Na^+\) et \(Cl^-\).

Lorsqu’il se déplace dans l’enceinte à la vitesse \(V\), tous les ions ont, en plus de leur vitesse propre d’agitation thermique, une composante commune de vitesse \(V\) dans la direction du mouvement, d’où résulte l’énergie cinétique de translation.

Après le choc sur la paroi, cette composante commune a disparu : l’énergie de translation n’est pas perdue, mais a servi à accroître l’énergie d’agitation thermique. Ce qui veut dire que la portion commune \(V\) de la vitesse des divers ions s’est transformée en un ensemble de vitesses dirigées dans toutes les directions, de façon désordonnée. Il est clair qu’il n’y a aucune chance pour que tous ces petits suppléments de vitesse viennent d’eux-mêmes à se trouver tous dirigés parallèlement, reconstituant la vitesse d’ensemble \(V\) du cristal.

En d’autres termes, il est très facile de passer d’un ensemble ordonné de vitesses réparties au hasard, mais l’inverse n’est pas possible, ou plutôt est extrêmement peu probable.

Nous avons ici un premier exemple naturel de l’ordre vers le désordre, alors que l’évolution inverse, du désordre vers l’ordre, est quasiment impossible pour un système isolé, c’est-à-dire sans qu’intervienne une force extérieure.

Considérons maintenant un récipient adiabatique et indéformable séparé par une vanne en deux parties remplies séparément et à pression atmosphérique, l’une d’hydrogène et l’autre d’oxygène. En ouvrant la vanne, les deux gaz diffusent l’un dans l’autre de façon irréversible.

Il est clair qu’une fois le mélange réalisé, nous pouvons attendre indéfiniment avant de voir, par suite de l’agitation moléculaire, les molécules d’oxygène se rassembler toutes dans la moitié gauche et celles d’hydrogène dans la moitié droite.

En d’autres termes, le système isolé passe facilement de l’état ordonné (molécules rangées dans leurs compartiments respectifs) à l’état désordonné (molécules réparties au hasard dans les deux compartiments), mais il ne passera pas de lui-même de l’état désordonné à l’état ordonné : il y faudra une intervention extérieure (utilisation de membranes hémiperméables) et dépense de travail.

Il est alors possible d’étudier, à ce point de vue, tous les processus naturels et de reconnaître que le sens naturel des processus physiques est celui qui tend à augmenter le désordre de la portion de l’Univers intéressée par ce processus.

S’il s’agit d’un système isolé, le processus tendra à augmenter le désordre du système : par exemple, la dissipation de travail par frottement dans un liquide entouré d’une enceinte adiabatique augmente l’agitation thermique, donc le désordre du liquide.

Si le système est en relation avec une source de chaleur, c’est le désordre global de l’ensemble système – source de chaleur qui est accru. Par exemple, la dissipation de travail par frottement dans un liquide maintenu à température fixe par une source de chaleur augmente l’agitation thermique, donc le désordre de la source.

Rapprochons ce résultat de l’expression du second principe relative aux systèmes isolés : l’entropie d’un système isolé croît toujours dans un processus naturel. Elle croît donc toujours lorsque croît le désordre. Nous commençons à entrevoir que l’entropie d’un système est une mesure de son désordre moléculaire.

2. Entropie et information

Revenons à présent à la définition de l’état microscopique d’un système en mécanique statistique. Cet état est susceptible d’être obtenu par un nombre plus ou moins grand de complexions.

Dans la terminologie de Bolzmann, une complexion désigne une répartition ou une structure dans laquelle chaque molécule a une énergie cinétique donnée. La connaissance exacte de la complexion d’un système permettrait d’extraire de ce système tout ce qu’il est possible de savoir.

En d’autres termes, notre information sur le système est absolue, à condition évidemment que l’on ait choisi pour les cellules de l’extension en phase la dimension minimum compatible avec le principe d’incertitude de Heisenberg.

En fait, nous ne pouvons jamais connaître que l’état microscopique du système (nombre de molécules occupant le i° domaine, etc.). Si cet état est accessible à partir de \(W\) complexions, notre information sur le système nous laisse donc le choix entre \(W\) possibilités ; c’est là une information d’autant plus faible évidemment que \(W\) est plus élevé.

Un système évolue de lui-même de façon à rendre minimum notre information à son sujet, compte tenu évidemment des liaisons qui lui sont imposées.

L’entropie d’un système ne se conserve pas, d’où la difficulté à en donner une définition intuitive. Selon le second principe, l’entropie d’un système isolé ne peut pas diminuer : elle augmente mais peut reste constante si la transformation est réversible. Ainsi, l’information évoluant en sens inverse de l’entropie est une notion qui constitue l’un des fondements de la cybernétique.

Revenons à la notion de désordre. Il est clair que si un système est dans un état microscopique qui ne peut être réalisé que par une seule complexion, la connaissance de l’état implique automatiquement la connaissance de la complexion du système et par suite une déformation absolue sur ce système.

Cette connaissance absolue du système nous permet de prévoir exactement son comportement dans ses plus infimes détails ; l’état du système est alors parfaitement ordonné. Si par contre, l’état peut être réalisé par \(W\) complexions entre lesquelles il nous est impossible de choisir, nous serons incapables de prévoir exactement le comportement du système à l’échelle microscopique et nous devrons considérer cet état comme d’autant plus désordonné que \(W\) est plus grand.

En conclusion, l’entropie d’un système est une fonction croissante de son désordre moléculaire. Ce désordre moléculaire est lui-même une fonction croissante du nombre de complexions que nous avons aussi désigné sous le nom de probabilité de l’état. Il existe donc entre entropie \(S\) d’un système et la probabilité \(W\) de son état microscopique, la relation : \[S~=~f(W)\]

La fonction \(f\) est une fonction croissante dont nous allons nous proposer de déterminer la forme.

3. Relation Entropie - Probabilité

Considérons deux systèmes \(A\) et \(B\). L’état microscopique de \(A\) peut être réalisé par \(W_1\) complexions et celui de \(B\) par \(W_2\) complexions.

L’état microscopique de l’ensemble \(AB\) peut être réalisé en associant une complexion quelconque de \(A\) (faisant partie de la série des \(W_1\) complexions de \(A\)) à une complexion quelconque de \(B\) (faisant partie de la série des \(W_2\) complexions de \(B\)). Soit au total \(W_1~W_2\) possibles.

L’état microscopique de l’ensemble \(AB\) peut donc être réalisé à partir de \(W = W_1~W_2\) complexions distinctes.

On a donc : \[W(AB)=W(A)~W(B)\]

Par ailleurs l’entropie de l’ensemble \(AB\) est : \[S(AB)=S(A)+S(B)\]

Nous en déduisons que la fonction \(f\) satisfait à la relation : \[f(W_1~W_2)=f(W_1)+f(W_2)\]

En dérivant par rapport à \(W_2\) en laissant \(W_1\) fixe : \[W_1~f'(W_1~W_2)=f'(W_2)\]

Puis dérivant cette relation par rapport à \(W_1\) (\(W_2\) fixe) : \[W_1~W_2f''(W_1~W_2)+f'(W_1~W_2)=0\]

La fonction \(f\) satisfait donc à la relation fonctionnelle : \[x~f''(x)+f'(x)=0\qquad\text{soit :}\quad \frac{f''}{f'}(x)=-\frac{1}{x}\]

Par intégration, on obtient successivement : \[\ln[f'(x)]=-\ln(x)+\ln(A)\quad;\quad A=cte\]

Soit :

\[\begin{aligned} &f'(x)=\frac{A}{x}\\ &f(x)=A~\ln(x)+B\end{aligned}\]

Avec \(B=0\) en raison de la relation initiale : \[f(W_1~W_2)=f(W_1)~f(W_2)\]

nous sommes conduits à poser : \[S=A~\ln(W)\]

On pourrait penser qu’il convient d’ajouter au second membre une constante arbitraire \(S_0\) destinée à représenter la constante additive arbitraire de l’entropie. Nous allons montrer que c’est inutile, celle-ci étant déjà contenue dans \(\ln(W)\).

Nous avons déjà remarqué que le nombre de complexions \(W\) qui correspond à un état donné dépend essentiellement du volume \(d\tau\) choisi pour les cellules de l’extension en phase : or, ce volume a été choisi à priori de façon arbitraire.

Divisons alors par un même facteur \(r\) le volume de toutes les cellules qui devient \(d\tau / r\), les domaines restant inchangés (et par suite les degrés d’occupation \(N_i\) correspondant à chaque état microscopique). Tous les \(g_i\) se trouvent multipliés par le même facteur \(r\).

Reprenons alors l’expression : \[\ln(W)=\sum_{i=1}^D \Big\{N_i~\ln\frac{N_i+g_i}{N_i}+g_i~\ln\frac{N_i+g_i}{g_i}\Big\}\]

Lorsque \(g_i\gg N_i\) et que, par suite : \[\ln\frac{N_i+g_i}{N_i}\approx \ln\frac{g_i}{N_i}\quad;\quad \ln\frac{N_i+g_i}{g_i}\approx \ln\frac{N_i}{g_i}\]

elle s’écrit alors : \[\ln(W)=\sum_{i=1}^D N_i \Big\{1+\ln\Big(\frac{g_i}{N_i}\Big)\Big\}\]

Multiplier les \(g_i\) par \(r\) sans toucher aux \(N_i\) revient à ajouter à \(\ln (W)\) la quantité : \[\sum_{i=1}^D N_i~\ln(r)=N~\ln(r)\]

ou si l’on veut à multiplier \(W\) par \(r^N\).

\(r\) étant à priori arbitraire, \(W\) n’est défini qu’à une constante multiplicative près et par suite \(\ln(W\)) n’est défini qu’à une constante additive près qui suffit donc à représenter la constante additive de l’entropie.

4. Formule de Boltzmann

4.1. Cas du gaz parfait

Nous allons maintenant calculer la valeur de la constante \(A\) en nous plaçant dans le cas particulier d’une mole de gaz parfait.

Supposons que nous fassions subir à cette mole la détente de Joule (sans travail, adiabatique et isotherme) du volume \(V\) au volume \(2~V\).

La variation d’entropie du gaz est la même que si la détente avait eu lieu de façon isotherme et réversible. Soit comme nous l’avons vu plus haut : \[S_F-S_I=R~\ln(2)\]

Cherchons l’augmentation du nombre de complexions de l’état microscopique du gaz. Dans ce but, nous considérons notre mole de gaz, qui contient \(N = 6,02 \times 10^{23}\) molécules, dans l’état final où elle emplit les deux moitiés du récipient de volume total \(2~V\).

Par suite de l’agitation moléculaire, la complexion de cette assemblée de molécules change constamment. Le gaz choisit constamment une nouvelle complexion parmi un nombre immense de complexions également probables. L’état microscopique évolue constamment, l’assemblée ayant beaucoup plus de chances de tomber sur un état accessible par beaucoup de complexions que sur un état accessible par peu de complexions.

Cherchons par exemple la probabilité pour que soit atteint un état où toutes les molécules se trouvent rassemblées dans la moitié gauche du récipient, reconstituant ainsi l’état initial observé avant la détente. Les molécules sont sans interaction et non soumises à un champ de forces.

Le fait que l’énergie totale doit rester constante n’impose donc nullement une place privilégiée dans l’enceinte aux diverses molécules qui ont autant de chances de se trouver dans la moitié gauche que dans celle de droite.

Il y a donc :

• 1 chance sur 2 pour que la molécule 1 se trouve dans la moitié gauche,

• 1 chance sur 2 pour que les molécules 1 et 2 y soient.

En définitive \(1/2^N\) chance pour que toutes les molécules y soient rassemblées.

Le nombre \(2^N\) est tellement grand qu’il dépasse l’imagination ; nous pouvons donc affirmer pratiquement qu’il n’y a aucune chance pour que le gaz retourne de lui-même à son état initial, ce que l’on observe expérimentalement.

Revenons au calcul. Parmi toutes les dispositions possibles des molécules, il n’y a donc qu’une proportion \(1/2^N\) qui les rassemble toutes dans la moitié gauche. Ceci revient à dire que l’état initial \(I\) du gaz est satisfait par un nombre de complexions \(W_I~2^N\) fois plus petit que le nombre de complexions \(W_F\) qui correspond à l’état final.

Nous avons donc : \[\frac{W_F}{W_I}=2^N\qquad\text{soit encore :}\quad \ln(W_F)-\ln(W_I)=N~\ln(2)\]

Rapprochant ceci de la relation : \[S_F-S_I=R~\ln(2)\]

Et remplaçant \(S\) par \(A~\ln(W)\) \[A~\{\ln(W_F)-\ln(W_I)\}=R~\ln(2)\]

Il vient : \[A=\frac{R}{N}=k\qquad\text{constante de Boltzmann}\]

Nous arrivons donc à la relation extrêmement importante (formule de Boltzmann) : \[S=k~\ln(W)\]

4.2. Cas d’un système quelconque

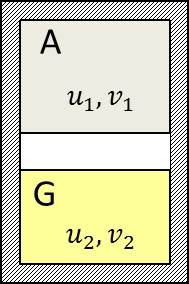Supposons pour simplifier un système chimique, sensible aux seules forces de pression. Soit \(A\) ce système que nous plaçons en compagnie d’un gaz parfait \(G\) au sein d’une enceinte commune, adiabatique et indéformable.

Le gaz et le système sont séparés par un piston diatherme pouvant coulisser sans frottement dans le corps de pompe formé par l’enceinte adiabatique. Nous laissons s’établir l’équilibre mécanique et thermique : \(G\) et \(A\) ont alors même pression et même température \(T\).

Définissons alors l’état macroscopique de \(G\) par son volume \(V_1\) et son énergie interne \(U_1\). Celui de \(A\) sera défini par son volume \(V_2\) et son énergie interne \(U_2\).

Envisageons une petite modification réversible de l’état de \(A\) et de celui de \(G\). Elle sera produite en déplaçant le piston d’une quantité infiniment petite et en faisant passer à travers lui une quantité de chaleur infiniment petite.

Soit \(S_1\) l’entropie de \(G\) et \(S_2\) celle de \(A\).

Nous pouvons écrire :

\[\begin{aligned} &T~dS_1=dU_1+p~dV_1\\ &T~dS_2=dU_2+p~dV_2\end{aligned}\]

Remarquons alors que \(S_1\) est lié au nombre de complexions \(W_1\) de l’état microscopique de \(G\) par la relation : \[S_1=k~\ln(W_1)\]

Et introduisons la quantité : \[S'_2=k~\ln(W_2)\]

\(W_2\) : nombre de complexions correspondant à l’état de A.

Le nombre de complexions de l’ensemble \([G,~A\)] est\(W = W_1~W_2\) et ce nombre est maximum puisque l’ensemble est à l’équilibre thermodynamique, ce qui veut dire que pour toute modification interne de l’ensemble \([G,~A]\) isolé mécaniquement et au point de vue thermodynamique, \(W\) reste stationnaire.

On a donc :

\[\begin{aligned} k~d[\ln(W_1~W_2)]&=dS_1+dS'_2\\ dS'_2&=-\frac{1}{T}~(dU_1+p~dV_1)\end{aligned}\]

Par ailleurs :

\[\begin{aligned} dU_1+dU_2&=0 &&\text{énergie totale constante}\\ dV_1+dV_2&=0 &&\text{volume total constant}\end{aligned}\]

On a donc : \[dS'_2=\frac{1}{T}~(dU_2+p~dV_2)\]

Ce qui montre que \(dS’_2\) s’exprime exactement de la même façon que \(dS_2\) en fonction des variables thermodynamiques \(U_2\) et \(V_2\) de \(A\).

\(S_2\) n’étant définie qu’à une constante additive près, la fonction \(S'_2=k.\ln(W)\) s’identifie donc à l’entropie du système \(A\).

Ceci démontre dans le cas général d’un système chimique quelconque la relation de Boltzmann : \[S=k~\ln(W)\]

Nous admettrons qu’elle est valable pour un système absolument quelconque.

Exercice

Vérifions par exemple que l’absorption d’une quantité de chaleur \(dQ\) par une assemblée de molécules enfermée dans une enceinte indéformable diatherme, à l’équilibre avec un thermostat de température \(T\), entraîne une variation \(dS = dQ/T\) de la fonction \(S = k~\ln(W)\).

Les molécules ne peuvent recevoir de travail que des forces de pression ; l’enceinte étant indéformable, seul un apport de chaleur peut modifier l’énergie totale de l’assemblée. Nous avons donc \(dU = dQ\).

La température reste constante, ou plus exactement varie d’une quantité infiniment petite \(dT\). La répartition des molécules dans les divers domaines de l’extension en phase est donnée par : \[\frac{N_i+g_i}{N_i}=\alpha+\beta~U_i\quad;\quad\beta=\frac{1}{k~T}\]

L’énergie totale varie de : \[dQ=\sum_i U_i~dN_i\]

Par ailleurs : \[dS=d[k~\ln(W)]=k~d[\ln(W)]\]

Mais nous avons vu que : \[d[\ln(W)]=\sum_{i=1}^D \ln\frac{N_i+g_i}{N_i}~dN_i=\sum_{i=1}^D(\alpha+\beta~U_i)~dN_i\]

Or : \[\sum N_i=N=cte\quad\Rightarrow\quad\sum dN_i=0\]

Il vient donc : \[d[\ln(W)]=\beta\sum U_i~dN_i=\beta~dQ=\frac{dQ}{k~T}\]

On a donc bien: \[dS=d[k~\ln(W)]=\frac{dQ}{T}\]

5. Caractère statistique du second principe

Sous sa forme classique, le second principe exprimait l’impossibilité pour un système isolé de retourner à son état initial. L’interprétation statistique que nous en avons donnée est moins catégorique en apparence puisqu’elle montre simplement qu’il y a très peu de chances pour qu’un système (par exemple le gaz parfait ayant subi la détente de Joule) retourne de lui-même à son état initial.

Il n’y a qu’une chance sur \(2^N\) pour que les \(N\) molécules d’un gaz parfait se rassemblent d’elles-mêmes dans la moitié de gauche du récipient qui les contient. Si \(N\) est égal au nombre d’Avogadro, nous avons la quasi-certitude que ce phénomène ne se produira jamais. Toutefois, s’il n’y avait que 5 molécules (par exemple) dans le récipient, leur rassemblement dans la moitié gauche se produirait plus souvent.

La même remarque se présente si on recherche la probabilité pour que les concentrations moléculaires dans les deux moitiés du récipient diffèrent d’une certaine quantité (2 \(\varepsilon\) en valeur relative). Cela revient à rechercher le nombre de complexions conduisant à un état où la moitié de gauche contient \(N(1-\varepsilon)/2\) molécules et celle de droite \(N(1+\varepsilon)/2\).

Le nombre de distributions des molécules conduisant à cet état est alors : \[W=\frac{N!}{\{N~(1-\varepsilon)/2\}!~\{N~(1+\varepsilon)/2\}!}\]

On obtient, tous calculs faits : \[\ln(W)\approx N~\ln(2)-\frac{N~\varepsilon^2}{2}\]

\(W\) est maximum et égal à \(W_0\) pour \(\varepsilon=0\).

La probabilité relative \(W/W_0\) pour que la concentration moléculaire dans l’un des demi récipients dépasse de \(\varepsilon\) en valeur relative moyenne est donc : \[\frac{W}{W_0}=\exp\Big(\frac{-N~\varepsilon^2}{2}\Big)\]

\(N\) est de l’ordre de \(10^{22}\) (récipient de 1 litre à la pression atmosphérique), nous n’avons donc aucune chance d’observer des valeurs de \(\varepsilon\), même aussi faibles que \(10^{-9}\).

Il sera quand même normal d’observer des variations spontanées de concentration \(\varepsilon\) (et par suite de pression dans chacun des demi-récipients) de l’ordre de \(1/\sqrt{N}\).

De telles variations spontanées de pression seraient inacceptables malgré leur très faible valeur, dans le cadre rigide du second principe sous sa forme classique. Elles ont lieu cependant, le second principe n’ayant qu’une valeur statistique et ne régissant que les phénomènes macroscopiques.

Nombreux sont les exemples de phénomènes microscopiques ne satisfaisant pas au second principe.

Citons par exemple le cas du mouvement brownien, ou mieux celui d’un pendule ordinaire qui, abandonné à lui-même, conserve une oscillation erratique d’amplitude extrêmement faible et d’énergie moyenne \(k~T\) (équipartition), énergie tirée d’une seule source de chaleur.

Objections au second principe

Nous analyserons pour terminer deux objections que l’on a pu formuler à l’encontre du second principe.

La première concerne l’expérience de Joule ; nous laissons s’écouler le gaz d’un récipient à l’autre et constatons par exemple à un moment donné une certaine répartition de vecteurs vitesse et de position de molécules. Sans rien toucher aux positions de molécules donnons aux vitesses des valeurs exactement opposées.

Les lois de la mécanique étant strictement réversibles, les molécules, refaisant leur chemin en sens inverse, vont venir se rassembler dans le premier récipient ; on ferme la vanne et le tour est joué : le gaz a subi l’évolution inverse de son évolution initiale, sans aide extérieure.

Il faut bien admettre qu’il en serait ainsi si le gaz tombait de lui-même sur une des complexions obtenues en renversant les vitesses à partir d’une des complexions qu’il traverse effectivement, mais il n’y a aucune chance pour que le gaz tombe sur une telle complexion, la probabilité d’obtention d’une complexion donnée étant infiniment faible.

La seconde observation, toujours relative à l’expérience de Joule, consiste à faire garder la vanne qui sépare les deux moitiés du récipient par un personnage extrêmement petit et habile, désigné sous le nom de démon de Maxwell.

Ce démon serait capable de trier les molécules suivant les vitesses auxquelles elles arrivent au niveau de l’ouverture et d’ouvrir la vanne pour laisser uniquement vers la droite les molécules rapides et uniquement vers la gauche les molécules lentes. Au bout d’un certain temps, la température située à droite est plus élevée que celle de gauche, en contradiction avec le second principe qui demande, au contraire, l’égalisation des températures.

Il ne faut évidemment pas considérer ceci comme une objection valable au second principe. Le démon de Maxwell n’existe pas dans la nature. Il est donc normal que son intervention viole le second principe qui, rappelons-le, sépare les phénomènes naturels des phénomènes non naturels (on serait ici tenté de dire surnaturels). L’objection ne prendrait du poids que si un dispositif réalisable pouvait effectuer le tri des molécules de cette manière, et nous n’en connaissons pas.