1. Introduction

Nous désignons sous le nom de phase toute substance chimique homogène, c’est-à-dire qui présente en tout point les mêmes propriétés physiques et chimiques. La phase peut être à l’état liquide, solide ou gazeux ; elle peut être formée d’un corps pur ou d’un mélange. S’il s’agit d’un mélange toutefois, celui-ci doit être assez intime pour que tout élément de volume, si petit soit-il, présente la même composition que l’ensemble.

Deux solides ne pourront par exemple jamais être mélangés par broyage assez intimement pour former une phase unique ; on pourra par contre arriver à former une phase unique à partir de deux métaux, par exemple en les fondant ensemble, si les rapports de masse sont tels qu’on puisse au refroidissement obtenir une solution solide, c’est-à-dire un mélange à l’état moléculaire.

Soit alors une telle phase, de composition et de masse déterminée et dans laquelle nous supposons qu’aucune réaction chimique n’intervient. Tout état d’équilibre thermodynamique de cette phase pourra être défini par la connaissance de deux quelconques des trois variables d’état \(p,~v,~T\).

Nous pourrons comme pour les fluides homogènes introduire les coefficients calorimétriques \(C_p,~C_v,~h,~l,~\lambda,~\mu\) et exprimer à partir de ces coefficients les différentielles des fonctions \(U,~H,~S\) sous la forme par exemple :

\[\begin{aligned} &dU=C_v~dT +(l-p)~dv\\ &dH=C_p~dT +(h+v)~dp\\ &dS=\frac{C_v}{T}~dT+\frac{l}{T}~dv=\frac{C_p}{T}~dT+\frac{h}{T}~dp\end{aligned}\]

Nous pouvons aussi remarquer que, pour tout état d’équilibre, les diverses fonctions d’état \(p,~v,~T,~U,~H,~S,~F,~G\) ont des valeurs parfaitement déterminées (une fois choisies les constantes additives de l’énergie interne et de l’entropie).

Nous observons alors que la connaissance de deux de ces quantités suffit à fixer toutes les autres, ce qui revient à dire que deux quelconques de ces fonctions d’état peuvent être choisies pour constituer les coordonnées thermodynamiques de la phase (sauf cas exceptionnel où elles ne sont pas indépendantes, par exemple \(V,~T\) pour un gaz parfait).

2. Transformations infinitésimales. Equations de Maxwell

Toute transformation infinitésimale sera parfaitement définie par deux quelconques de l’ensemble des variations infiniment petites \(dp,~dv,~dT,~dU,~dH,~dS,~dF,~dG\). Nous pouvons par exemple exprimer \(dU,~dH,~dF,~G\) sous la forme :

\[\begin{aligned} &dU=T~dS-p~dv\\ &dH=T~dS+v~dp\\ &dF=-S~dT-p~dv\\ &dG=-S~dT+v~dp\end{aligned}\]

Ces différentielles sont des différentielles totales d’où résultent les équations de Maxwell qu’il est inutile de retenir parce qu’elles sont très faciles à retrouver :

\[\begin{aligned} &\Big(\frac{\partial T}{\partial v}\Big)_S =-\Big(\frac{\partial p}{\partial S}\Big)_v\\ &\Big(\frac{\partial T}{\partial p}\Big)_S =-\Big(\frac{\partial v}{\partial S}\Big)_p\\ &\Big(\frac{\partial S}{\partial v}\Big)_T =\Big(\frac{\partial p}{\partial T}\Big)_v\\ &\Big(\frac{\partial S}{\partial p}\Big)_T =-\Big(\frac{\partial v}{\partial T}\Big)_p\end{aligned}\]

3. Formules de Clapeyron

Les relations :

\[\begin{aligned} &T~dS=C_v~dT+l~dv\\ &T~dS=C_p~dT+h~dp\end{aligned}\]

peuvent s’exprimer sous une forme décomposée :

\[\begin{aligned} &T~\Big(\frac{\partial S}{\partial v}\Big)_T=l\\ &T~\Big(\frac{\partial S}{\partial p}\Big)_T=h\\ &T~\Big(\frac{\partial S}{\partial T}\Big)_v=C_v\\ &T~\Big(\frac{\partial S}{\partial T}\Big)_p=C_p\end{aligned}\]

En comparant aux deux dernières relations de Maxwell, nous obtenons les formules de Clapeyron :

\[\begin{aligned} &l~=~T~\Big(\frac{\partial p}{\partial T}\Big)_v\\ &h~=~-T~\Big(\frac{\partial v}{\partial T}\Big)_p\end{aligned}\]

On a également:

\[\begin{aligned} &\frac{\partial C_v}{\partial v}~=~T~\frac{\partial^2p}{\partial T~\partial v}\\ &\frac{\partial C_p}{\partial p}~=~T~\frac{\partial^2S}{\partial T~\partial v}\end{aligned}\]

Soit en comparant aux deux dernières relations de Maxwell :

\[\begin{aligned} &\frac{\partial C_v}{\partial v}~=~T~\frac{\partial^2p}{\partial T^2}\\ &\frac{\partial C_p}{\partial p}~=-~T~\frac{\partial^2v}{\partial T^2}\end{aligned}\]

Ces relations sont très générales et valables pour une phase quelconque. Nous pouvons encore, remplaçant \(l\) par sa valeur dans la relation générale : \[l=(C_p-C_v)~\Big(\frac{\partial T}{\partial p}\Big)_v\]

obtenir la relation : \[C_p-C_v~=~T~\Big(\frac{\partial p}{\partial T}\Big)_v~\Big(\frac{\partial v}{\partial T}\Big)_p\]

Enfin, en remarquant que : \[\Big(\frac{\partial p}{\partial T}\Big)_v= -\Big(\frac{\partial p}{\partial v}\Big)_T~\Big(\frac{\partial v}{\partial T}\Big)]_p\]

on peut encore écrire : \[C_p-C_v=-T~\Big(\frac{\partial v}{\partial T}\Big)^2_p~\Big(\frac{\partial p}{\partial v}\Big)_T\]

Introduisant les coefficients de dilatation :

\[\begin{aligned} &\alpha~=~+\frac{1}{v}~\Big(\frac{\partial v}{\partial T}\Big)_p\\ &\chi~=~-\frac{1}{v}~\Big(\frac{\partial v}{\partial p}\Big)_T\end{aligned}\]

on peut écrire ; \[C_p-C_v~=~T~v~\frac{\alpha^2}{\chi}\]

Ceci montre, \(\chi\) étant toujours positif, que \(C_p>C_v\).

Remarque

Nous n’avons pas eu besoin de nous restreindre à des transformations infinitésimales réversibles. Il est clair en effet que la variation d’une fonction d’état dans une transformation joignant deux états d’équilibre est exactement la même, que la transformation soit réversible ou non. Nous pourrons toujours écrire par exemple dans une transformation \([dv,~dT]\) : \[T~dS = C_v~dT+l~dv\]

Ceci, même si la variation de température a été obtenue en imprimant au moyen d’un piston de vibration prolongée au fluide supposé visqueux, et sans emprunt de chaleur à la source pendant la transformation : tout ce qui est nécessaire est que les états initial et final soient des états d’équilibre.

Par contre, ce n’est que si la transformation infinitésimale est réversible que l’on peut écrire : \[dQ = C_v~dT+l~dv\qquad;\qquad dW = -p~dv\]

Toutes ces relations s’appliquent parfaitement aux solides, à condition que les transformations infinitésimales envisagées restent dans le domaine élastique.

Soit par exemple à déterminer le coefficient de compressibilité isotherme d’un métal donné. La relation de Reech s’applique dans le domaine élastique : \[\frac{\chi}{\chi'} = \frac{C_p}{C_v}\]

En combinant à : \[C_p-C_v = T~v~\frac{\alpha^2}{\chi}\]

Par élimination de \(C_v\), nous obtenons : \[\frac{C_p-C_v}{C_p} = \frac{\chi-\chi'}{\chi}=\frac{T~v~\alpha^2}{\chi~C_p}\]

Le coefficient \[\chi = \chi'+T~v~\frac{\alpha^2}{C_p}\]

peut être déduit de mesures du coefficient de dilatation linéaire à pression constante ; soit \(k\) ce coefficient (on suppose le liquide isotrope). On a alors \(\alpha=3~k\).

\(C_p\) se déduit des mesures calorimétriques et \(\chi'\) de la mesure de la vitesse de propagation du son dans le solide.

4. Application des formules de Clapeyron

4.1. Application aux gaz parfaits

Nous obtenons immédiatement : \[l=T~\frac{\partial p}{\partial T}=p\qquad;\qquad h=-T~\frac{\partial v}{\partial T}=-v\]

ce qui montre qu’un fluide dont l’équation d’état est \(p~v-r~T=0\) satisfait automatiquement à la première et à la seconde loi de Joule (variation de température nulle dans la détente de Joule-Gay Lussac et dans la détente Joule-Kelvin).

Inversement, nous allons montrer qu’un gaz qui satisfait à ces deux lois admet l’équation d’état \(p~v=r~T)\).

La loi de Gay Lussac exige que : \[U~=~f(T)\qquad\text{soit :}\quad l~=~p\qquad\text{donc :}\quad T~\Big(\frac{\partial p}{\partial T}\Big)_v~=~p\]

On en tire : \[\Big(\frac{\partial T}{\partial p}\Big)_v~=~\frac{T}{p}\]

La deuxième loi de Joule exige que : \[H~=~g(T)\qquad\text{soit :}\quad h~=~-v\qquad\text{donc :}\quad T~\Big(\frac{\partial v}{\partial T}\Big)_p~=~v\]

On en tire : \[\Big(\frac{\partial T}{\partial v}\Big)_p~=~\frac{T}{v}\]

La température \(T\) est fonction de \(p,~v\), soit \(T=T(p,~v)\)

On a pour un fluide quelconque : \[dT=\Big(\frac{\partial T}{\partial p}\Big)_v~dp+\Big(\frac{\partial T}{\partial v}\Big)_p~dv\]

Ce qui donne pour un gaz satisfaisant aux deux lois de Joule : \[dT=\frac{T}{p}~dp+\frac{T}{v}~dv\quad\Rightarrow\quad \frac{dT}{T}=\frac{dp}{p}+\frac{dv}{v}=\frac{d(p~v)}{p~v}\]

En intégrant : \[\ln(T)=\ln(p~v)+cte\quad\Rightarrow\quad p~v=r~T\]

4.2. Énergie interne, enthalpie et entropie d’un gaz parfait

Des différentielles :

\[\begin{aligned} dU&=C_v~dT\\ dS&=\frac{C_p}{T}~dT+\frac{p}{T}~dv=C_v~\frac{dT}{T}+\frac{n~R}{v}~dv\\ dH&=C_p~dT\\ dS&=\frac{C_p}{T}~dT-\frac{(-v)}{T}~dp=C_p~\frac{dT}{T}-\frac{n~R}{p}~dp\end{aligned}\]

nous tirons :

\[\begin{aligned} U&=U_0+\int_{T0}^T C_v~dT\\ S&=S_0+\int_{T0}^T \frac{C_v}{T}~dT+n~R~\ln(v)\\ H&=H_0+\int_{T0}^T C_p~dT\\ S&=S'_0+\int_{T0}^T \frac{C_p}{T}~dT-n~R~\ln(p)\end{aligned}\]

\(U_0\) et \(H_0\) étant les valeurs arbitrairement choisies pour l’énergie interne et l’enthalpie à la température \(T_0\), \(S_0\) et \(S'_0\) étant respectivement les valeurs arbitrairement choisies pour l’entropie dans l’état origine \((T=T_0;~v=1)\) ou dans l’état \((T=T_0;~p=1)\).

Les constantes étant arbitraires, nous pourrons écrire en omettant de spécifier les conditions de l’état origine :

\[\begin{aligned} U&=U_0+\int C_v~dT\\ S&=S_0+\int \frac{C_v}{T}~dT+n~R~\ln(v)\\ H&=H_0+\int C_p~dT\\ S&=S'_0+\int \frac{C_p}{T}~dT-n~R~\ln(p)\end{aligned}\]

Expressions simplifiées

S’il s’agit d’un gaz monoatomique, ou d’une façon générale si l’intervalle de température considéré est assez faible pour que l’on puisse considérer comme constantes les capacités calorifiques \(C_p,~C_v\), on pourra écrire approximativement :

\[\begin{aligned} U&=U_0+C_v~T\\ H&=H_0+C_p~T\\ S&=S_0+C_v~\ln(T)+n~R~\ln(v)\\ \text{ou}\\ S&=S'_0+C_p~\ln(T)-n~R~\ln(p)\end{aligned}\]

Rappelons que les constantes additives \(U_0,~H_0~;~S_0,~S'_0\) sont arbitraires et pourront être déterminées par exemple en fixant arbitrairement l’énergie interne et l’entropie d’un état d’équilibre déterminé.

Remarquons également que les constantes \(U_0,~H_0\) doivent être choisies à la même valeur puisque : \[H-U=p~v=n~R~T=(C_p-C_v)~T\]

4.3. Variation d’entropie dans la détente isotherme d’un gaz parfait

Soit \(T\) la température constante. Dans une détente isotherme faisant passer le gaz de l’état \((p_0,~v_0)\) à l’état \((p,~v)\), la variation d’entropie est : \[S=n~R~\ln\Big(\frac{v}{v_0}\Big)=-n~R~\ln\Big(\frac{p}{p_0}\Big)\]

Si la détente est réversible, la chaleur reçue par le gaz est : \[Q=\int T~dS=n~R~\ln\Big(\frac{v}{v_0}\Big)=-n~R~\ln\Big(\frac{p}{p_0}\Big)\]

Le travail reçu étant : \[W=-n~R~T~\ln\Big(\frac{v}{v_0}\Big)=n~R~T~\ln\Big(\frac{p}{p_0}\Big)\]

Nous vérifions bien que : \[\Delta U=W+Q=0\]

Notons bien que si la détente est irréversible, l’égalité \(dQ=T~dS\) doit être remplacée par \(dQ<T~dS\). Par exemple dans la détente de Joule, nous aurons : \[Q<n~R~T~\ln\Big(\frac{v}{v_0}\Big)\]

ce qui est évidemment le cas puisque \(Q=0\).

Le gaz parfait subissant la détente de Joule voit son entropie augmenter, ce qui est normal puisqu’il s’agit d’un système isolé (\(W=Q=0\)) subissant une transformation irréversible.

4.4. Application au gaz de Van Der Waals

Prenons une mole d’un gaz satisfaisant à l’équation d’état Van Der Waals : \[\Big(p+\frac{a}{v^2}\Big)~(v-b)=R~T\]

La chaleur latente de dilatation est donnée par : \[l=T(\frac{\partial p}{\partial T})_v=T.\frac{R}{v-b}=p+\frac{a}{v^2}\]

On en déduit :

\[\begin{aligned} dU&=C_v~dT+\frac{a}{v^2}~dv\\ dS&=C_v~\frac{dT}{T}+R~\frac{dv}{v-b}\end{aligned}\]

Soit en intégrant :

\[\begin{aligned} U&=U_0+\int C_v~dT-\frac{a}{v}\\ S&=S_0+\int \frac{C_v}{T}~dT+R~\ln(v-b)\end{aligned}\]

On remarque également que : \[\Big(\frac{\partial C_v}{\partial v}\Big)_T=T~\Big(\frac{\partial^2p}{\partial T^2}\Big)_v=0\]

Pour un gaz de Van Der Waals, \(C_v\) ne dépend que de la température. (Rappelons que les gaz réels ne satisfont pas rigoureusement à l’équation de Van Der Waals.)

Détente adiabatique et réversible d’un gaz Van der Waals

Dans une détente adiabatique et réversible d’un gaz Van der Waals, l’entropie reste constante (on appelle aussi isentropique une telle détente). On a donc pour une détente infinitésimale d’une mole : \[dS=0\quad\Rightarrow\quad C_v~\frac{dT}{T}+R~\frac{dv}{v-b}=0\]

Si l’intervalle de températures décrit en cours de détente est assez faible pour qu’on puisse négliger la variation de \(C_v\) (qui ne dépend que de \(T\)), on pourra intégrer cette relation sous la forme : \[T^{Cv}~(v-b)^R=cte\]

qui peut s’écrire avec les variables \(p\) et \(v\) : \[\Big(p+\frac{a}{v^2}\Big)~(v-b)^{1+R/Cv}=cte\]

Cette équation généralise au gaz de Van der Waals, en la compliquant un peu, l’équation de Laplace obtenue pour la détente adiabatique et réversible d’un gaz parfait.

5. Détente de Joule-Kelvin

Considérons une détente Joule-Kelvin infinitésimale (c’est-à-dire correspondant à une chute de pression infiniment petite) d’un gaz réel. Le gaz passe de façon irréversible de l’état \((p,~T)\) à l’état \((p+dp,~T+dT)\) avec \(p<0\). Nous savons que l’enthalpie du gaz n’a pas changé.

La variation d’enthalpie serait évidemment la même dans une détente réversible (elle ne serait plus dans ce cas adiabatique) faisant passer le gaz du même état initial au même état final. On a de toute façon : \[dH=C_p~dT+(h+v)~dp=0\]

Nous désignerons sous le nom de coefficient Joule-Kelvin \(\mu\) du gaz le rapport des variations \(dT\) et \(dp\) dans la détente Joule Kelvin infinitésimale, soit : \[\mu=\Big(\frac{\partial T}{\partial p}\Big)_H\]

On a par suite : \[\mu=-\frac{1}{C_p}~(h+v)=\frac{1}{C_p}~\Big(T~\frac{\partial v}{\partial T}-v\Big)\]

que l’on peut encore écrire : \[\mu=\frac{v~T}{C_p}~\Big(\frac{1}{v}~\frac{\partial v}{\partial T}-\frac{1}{T}\Big)\]

soit en désignant par \(\alpha_0\) le coefficient de dilatation \(1/T\) du gaz parfait à la même température : \[\mu=\frac{v~T}{C_p}~(\alpha-\alpha_0)\]

Si \(\alpha>\alpha_0\), l’effet Joule-Kelvin est positif (refroidissement par détente).

Si \(\alpha<\alpha_0\), l’effet Joule-Kelvin est négatif (échauffement par détente).

Quand traverse la valeur \(\alpha_0\), il y a inversion de l’effet Joule-Kelvin.

6. Cas du gaz de Van der Waals

Nous représentons l’état du gaz dans le diagramme d’Amagat, en portant \(p\) en abscisse et \(p~v = y\) en ordonnée. L’équation de Van der Waals s’écrit, pour 1 mole : \[F(y,~p)=(y^2+a~p)(y-b~p)-R~T~y^2=0\]

Le lieu des points où le gaz suit la loi de Mariotte s’obtient en écrivant : \[\Big(\frac{\partial y}{\partial p}\Big)_T=-\frac{F'_p}{F_y}\qquad\text{soit :}\quad F'_p=0\]

On a donc en ces points : \[-b~(y^2+a~p)+a~(y-b~p)=0\]

C’est-à-dire : \[b~y^2-a~y+2~a~b~p=0\]

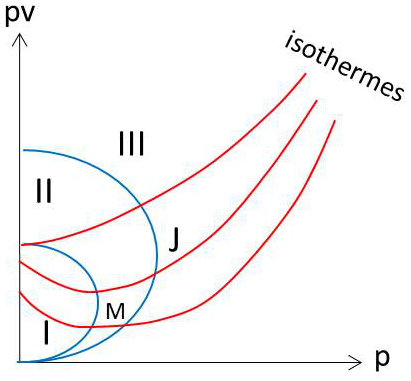On reconnaît l’équation d’une parabole \((M)\) passant par l’origine et par le point \((p=0,~y=a/b)\).

Cherchons également le lieu des points d’inversion de l’effet Joule-Kelvin. Nous écrivons qu’en tous ces points : \[\Big(\frac{\partial v}{\partial T}\Big)_p=\frac{v}{T}\]

Dérivons par rapport à \(T\) l’équation de Van der Waals, nous obtenons : \[\Big\{p+\frac{a}{v^2}-\frac{2~a}{v^3}~(v-b)\Big\}~\frac{\partial v}{\partial T}=R\]

Remplaçons dans cette relation \(\partial v/\partial T\) par \(v/T\) et multiplions par \(T\). Il vient : \[p+\frac{a}{v^2}-\frac{2~a}{v^2}~(v-b)=R~T\]

Comparons à la relation (équation de Van der Waals) : \[\Big(p+\frac{a}{v^2}\Big)~v-\Big(p+\frac{a}{v^2}\Big)~b=R~T\]

Nous obtenons par soustraction : \[\Big(p+\frac{a}{v^2}\Big)~b-2~a~p~(v-b)=0\]

Soit en multipliant par \(p~v^2\) et en remplaçant \(p~v=y\) : \[b~y^2-2~a~y+3~a~b~p=0\]

On reconnaît l’équation d’une parabole \((J)\) passant par l’origine et le point \((p=0,~y=2~a/b)\). La parabole \((J)\) est donc le lieu des points d’inversion de l’effet Joule-Kelvin.

Supposons alors que \(p\) augmente indéfiniment à température donnée \(T\). Alors \(v\) tend vers \(b\) quelque soit \(T\). Il en résulte qu’à toute température \(T > 0\) le rapport \(v/T\) tend vers \(b/T\), limite finie positive et que \((\partial v/\partial T)_p\) tend vers 0 quand \(p\) s’accroît indéfiniment : aux très fortes pressions \((\partial v/\partial T)_p-(v/T)<0\) et par suite \(\mu<0\). La région extérieure à la parabole \((J)\) correspond donc à l’échauffement par détente Joule-Kelvin.

Si nous partageons en trois régions I, II, III le diagramme par les paraboles \((M)\) et \((J)\), nous obtenons les résultats suivants : le gaz est plus compressible que les gaz parfaits dans la région I, moins compressible dans les régions II et III.

Le gaz a un effet Joule-Kelvin positif dans les régions I et II, négatif dans la région III.

Suivant la nature du gaz, les conditions ordinaires de température et de pression peuvent correspondre à un point figuratif situé dans l’une ou l’autre de ces trois régions.

7. Entropie de mélange

Nous avons jusqu’à présent considéré des substances homogènes de composition bien définie et nous sommes en mesure de calculer la variation d’entropie d’une telle substance lors d’une modification quelconque de la température, de la pression et du volume.

Nous allons maintenant envisager le mélange, à température et pression constante, de deux substances distinctes prises initialement à la même température et à la même pression en nous limitant tout de suite au cas de deux gaz parfaits distincts.

Le mélange de deux gaz parfaits s’accomplit de lui-même quand on établit une communication entre les récipients qui les contiennent. Dans l’état initial, les gaz \(G_1\) (\(n_1\) moles) et \(G_2\) (\(n_2\) moles) avaient séparément les entropies :

\[\begin{aligned} &S_1=S_0^1+\int C_{p1}~dT-n_1~R~\ln(p)\\ &S_2=S_0^2+\int C_{p2}~dT-n_2~R~\ln(p)\end{aligned}\]

L’entropie de l’ensemble des deux gaz pris séparément était \(S_1 + S_2\).

Laissons les gaz diffuser l’un dans l’autre à \(T\) et \(p\) constantes. L’entropie du mélange est : \[S_{mel}=S'_0+\int(C_{p1}+C_{p2})~dT-(n_1+n_2)~R~\ln(p)\]

mais ceci ne nous apprend rien sur la variation d’entropie qui a lieu lors du mélange, car rien pour le moment ne nous permet d’établir une relation entre \((S_0^1+S_0^2)\) d’une part et \(S'_0\) de l’autre. Même une étude expérimentale des conditions du mélange ne pourra nous renseigner, la diffusion étant une opération irréversible lorsqu’elle est ainsi réalisée.

Il va nous falloir procéder de façon réversible au mélange des deux gaz pour pouvoir en déduire la variation d’entropie qui l’accompagne.

Nous considérons alors deux récipients diathermes contenant respectivement \(n_1\) moles du gaz \(G_1\) et \(n_2\) moles du gaz \(G_2\) à la même pression \(p\). Tous deux sont maintenus par un thermostat commun à la même température \(T\). Les volumes occupés par \(G_1\) et \(G_2\) sont respectivement \(v_1\) et \(v_2\) et on a évidemment \(v_1/v_2 = n_1/n_2\).

Commençons par faire subir aux deux gaz une détente isotherme et réversible les faisant passer au volume final \(V = v_1 + v_2\). Les entropies des deux gaz ont varié respectivement de :

\[\begin{aligned} &S_1=n_1~R~\ln\Big(\frac{V}{v_1}\Big)=n_1~R~\ln\Big(\frac{n_1+n_2}{n_1}\Big)\\ &S_2=n_2~R~\ln\Big(\frac{V}{v_2}\Big)=n_2~R~\ln\Big(\frac{n_1+n_2}{n_2}\Big)\end{aligned}\]

Nous avons atteint un état, que nous désignerons sous le nom d’état de référence, dans lequel les deux gaz occupent séparément des volumes \(V = v_1 + v_2\) à la température \(T\).

Nous allons maintenant montrer qu’il est possible de passer de l’état où les deux gaz occupent ensemble le volume \(V\) à la température \(T\) (c’est-à-dire l’état qu’on aurait pu obtenir par simple diffusion irréversible des deux gaz à \(p\) et \(T\) constantes) au même état de référence, sans variation d’entropie.

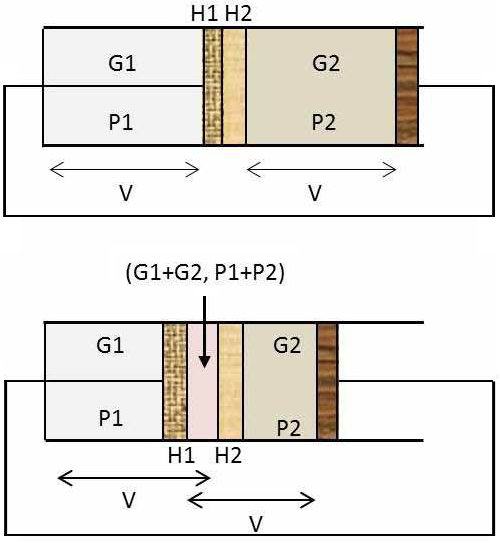Nous considérons dans ce but le récipient placé dans le vide de volume total \(2~V\) (figure ci-contre) formé d’un corps de pompe fermé à droite par un piston \(P\) qui peut coulisser sans frottement.

Le piston \(P\) est solidaire, par l’intermédiaire d’une liaison convenable, d’un piston hémiperméable \(H_1\) coulissant sans frottement) perméable au seul gaz \(G_1\) ; le volume compris entre \(P\) et \(H_1\) est constamment égal à \(V\).

Enfin, une cloison imperméable fixe \(H_2\) (perméable au seul gaz \(G_2\)) délimite à sa gauche un volume fixe égal à \(V\) dans le corps de pompe. Les cloisons \(H_1\) et \(H_2\) sont appliquées l’une contre l’autre à l’état initial.

Nous introduisons à gauche les \(n_1\) moles du gaz \(G_1\) et à droite les \(n_2\) moles du gaz \(G_2\). Plaçons le tout dans un thermostat de température \(T\) et commençons à déplacer lentement vers la gauche l’ensemble \((P,~H_1)\).

Le gaz \(G_1\) traverse librement la cloison \(H_1\) ; le gaz occupe toujours le même volume \(V\), de sorte que la pression de \(G_1\) reste constamment égale à sa pression initiale \(p_1\), de même que celle de \(G_2\) reste égale à \(p_2\).

Il en résulte qu’à tout moment la pression à gauche de \(H_1\) est \(p_1\), la pression à droite de \(H_2\) est \(p_2\) et la pression entre \(H_1\) et \(H_2\) est \(p_1 + p_2\), somme des pressions partielles des deux gaz.

\(\Sigma\) étant la section droite du corps de pompe, l’effort qui s’exerce sur \(H_1\) est dirigé vers la gauche et égal à : \[(p_1+p_2-p_2)~\Sigma =p_1~\Sigma\]

L’effort qui s’exerce vers la droite est égal à \(p_1~\Sigma\).

Au total, aucun effort ne s’exerce donc sur l’ensemble \((H_1,~p)\) qu’il est donc possible d’amener sans travail dans la position finale où \(H_1\) s’appuie sur le fond du corps de pompe et \(P\) sur \(H_2\). On a ainsi réalisé sans travail le mélange réversible de deux gaz de façon isotherme ; la variation d’énergie libre du système est donc nulle, soit : \[\Delta F=\Delta U-T~\Delta S\]

Or, \(\Delta U=0\) puisque l’ensemble de l’opération revient à faire passer de façon réversible et isotherme un ensemble de gaz parfaits du volume total \(2~V\) au volume \(V\). On a donc \(\Delta S=0\).

Ce qui montre qu’il n’y a pas de différence d’entropie entre le système formé par les deux gaz lorsque chacun d’eux occupe séparément un volume égal à \(V\) (état de référence) et le système formé par les deux gaz occupant ensemble ce même volume \(V\).

Désignons alors sous le nom d’entropie partielle du gaz \(G_1\) dans le mélange l’entropie qu’aurait ce gaz s’il occupait seul tout le volume du mélange ; de même pour le gaz \(G_2\). Le résultat que nous avons obtenu indique que l’entropie du mélange est la somme des entropies partielles des constituants \(G_1\) et \(G_2\).

Il se généralise immédiatement à un nombre quelconque de gaz parfaits et nous énoncerons ainsi le théorème de Gibbs :

L’entropie d’un mélange de gaz parfaits est la somme des entropies partielles des divers gaz constituants.

Revenant alors à la diffusion irréversible, à pression et température constantes, que nous avions considérée au début, nous voyons qu’il est possible de la conduire de façon irréversible au prix :

1. d’une détente isotherme faisant passer chacun des gaz séparément au volume final \(V\). Dans cette opération la variation d’énergie interne totale est nulle, et la variation d’entropie totale est, en posant

   \[\begin{aligned} &n1+n2=n\quad;\quad x_1=\frac{n_1}{n}\quad;\quad x_2=\frac{n_2}{n}\\ &\Delta S=n~R~\Big\{x_1~\ln\Big(\frac{1}{x_1}\Big)+x_2~\ln\Big(\frac{1}{x_2}\Big)\Big\}>0\end{aligned}\]

2. d’un mélange isotherme et réversible où les variations d’énergie interne et d’entropie du système sont nulles.

Au total, la diffusion irréversible à pression, température et volume total constants des deux gaz est une opération sans échange de travail avec le milieu extérieur et sans variation d’énergie interne, donc sans échange de chaleur avec l’extérieur. Le système des deux gaz est donc isolé et il est nécessaire que leur diffusion entraîne un accroissement d’entropie que nous avons pu chiffrer à : \[\Delta S=-R~\{n_1~\ln(x_1)+n_2~\ln(x_2)\}>0\]

\(x_1\) et \(x_2\) sont les concentrations moléculaires des gaz parfaits \(G_1\) et \(G_2\) dans le mélange final.

7.1. Diffusion de deux gaz parfaits identiques. Paradoxe de Gibbs

Écrivons l’entropie de mélange \(\Delta S\) sous la forme : \[\Delta S=-R~\Big\{n_1~\ln\Big(\frac{n_1}{n}\Big)+n_2~\ln\Big(\frac{n_2}{n}\Big)\Big\}\]

Dans cette formule n’apparaissent que des quantités indépendantes de la nature chimique des gaz \(G_1\) et \(G_2\) ; rien ne nous empêche donc à priori de l’appliquer à la diffusion de deux gaz identiques et de considérer par exemple que la diffusion de 3 moles d’oxygène dans 5 moles d’oxygène à \(p\) et \(T\) constantes entraîne une variation de l’entropie totale \[\Delta S=R~\Big\{\ln\frac{8}{3}+\ln\frac{8}{5}\Big\}\]

Ceci est évidemment absurde, l’état initial du système (8 moles d’oxygène à la pression \(p\) et à la température \(T\)) étant identique à l’état final. La formule ainsi écrite indique donc une variation d’entropie, alors qu’en fait il n’y en a pas. C’est en cela que consiste le paradoxe de Gibbs.

Remarquons en passant que le fait d’écrire la formule avec les concentrations moléculaires \(x_1\) et \(x_2\) indique déjà dans ce cas que quelque chose n’est pas normal. Ou bien \(x_1\) et \(x_2\) n’ont aucun sens physique, ou ils représentent tous deux la concentration de l’oxygène dans le mélange, auquel cas ils sont tous deux égaux à l’unité et la formule donne bien \(\Delta S=0\), mais alors la somme des concentrations est égale à 2 ce qui est absurde (par définition \(\sum x_i=1\)).

Remarquons d’autre part que le dispositif que nous avons imaginé pour calculer la variation d’entropie ne pourrait être réalisé dans le cas de deux gaz identiques, car il n’existe pas de cloison perméable à certaines molécules d’oxygène et imperméable à d’autres molécules d’oxygène rigoureusement identiques. L’entropie de diffusion s’évanouit donc lorsque les molécules qui diffusent deviennent indiscernables.

Ceci est en parfait accord avec les conceptions modernes de la mécanique quantique ; il est curieux de constater toutefois que l’indiscernabilité des systèmes identiques, notion généralement associée aux seuls raisonnements de la mécanique quantique, vient montrer son importance dans le phénomène classique de la diffusion de deux gaz.

Ce qui peut sembler vraiment étrange, c’est que la plus petite différence (isotopes par exemple) entre les molécules \(G_1\) et \(G_2\) fait apparaître l’entropie de mélange toujours la même tant que \(T,~n_1,~n_2\) restent les mêmes et que l’entropie de mélange s’évanouit lorsque cette différence infinitésimale devient rigoureusement nulle. Il y a là une discontinuité que l’on est peu accoutumé à rencontrer en physique classique. Cette discontinuité ne doit cependant pas nous étonner.

Imaginons en effet que nous puissions rendre progressivement de plus en plus semblables les molécules \(G_1\) et \(G_2\). Un observateur qui aurait à déterminer dans le mélange la nature (\(G_1\) ou \(G_2\)) de la molécule qui se trouve en un certain point aura de plus en plus de mal à le faire, mais on peut penser qu’en opérant avec des appareils de plus en plus soignés, il y arrivera toujours tant que subsistera une différence, si faible soit-elle, entre les molécules \(G_1\) et \(G_2\).

Il n’y arrivera certainement plus quand la différence disparaît complètement ; d’où une discontinuité dans les possibilités d’observation, ou encore d’information, sur l’état du mélange. Il n’est pas étonnant dès lors qu’à cette discontinuité corresponde une discontinuité dans l’entropie qui est une fonction d’état. Nous retrouvons en passant le lien étroit qui existe entre l’entropie et l’information.

En conclusion, le théorème de Gibbs est toujours applicable aux gaz parfaits à condition de ne considérer comme constituants du mélange que des constituants distincts, c’est-à-dire discernables, ce qui tombe sous le sens.

7.2. Entropie d’un mélange de gaz parfaits non réagissants

Soit alors un mélange en équilibre \((p,~T)\) contenant \(n_i\) moles du gaz parfait \(G_i\), etc. Nous introduisons les concentrations moléculaires des divers constituants : \[x_i=\frac{n_i}{\sum_i n_i}\]

Nous désignons par \(S_i^m\) l’entropie d’une mole du gaz \(G_i\) à \(T\) et \(p\). Nous avons : \[S_i^m=S_{0i}^m+\int \frac{C_{pi}}{T}~dT-R~\ln(p)\qquad\text{etc.}\]

L’entropie du système formé par les divers gaz pris séparément à la pression \(p\) et la même température \(T\) serait : \[S_{sep}=\sum_i n_i~\Big\{S_{0i}^m+\int\frac{C_{pi}}{T}~dT-R~\ln(p)\Big\}\]

En posant : \[\sigma_i=\frac{S_{0i}^m}{R}+\int\frac{C_{pi}}{T}~dT\qquad\sigma_i\text{ fonction de T seulement}\]

On peut écrire : \[S_{sep}=R~\sum_i n_i~\{\sigma_i-\ln(p)\}\]

Le mélange des gaz à la pression \(p\), de température \(T\), introduit l’entropie de mélange : \[S=-R~\sum_i \ln(x_i)\]

d’où il résulte que l’entropie du mélange des gaz parfaits à la température \(T\) et à la pression totale \(p\) est : \[S_{mel}=R~\sum_i n_i~\{\sigma_i-\ln(p)-\ln(x_i)\}\]

Ce qui peut aussi s’écrire : \[S_{mel}=R~\sum_i\{\sigma_i-\ln(p_i)\}\]

\(p_i\) désignant la pression partielle du gaz parfait \(G_i\) dans le mélange.

8. Fonction de Gibbs pour un gaz parfait

Nous considérons une mole de gaz parfait. Son enthalpie, son entropie et sa fonction de Gibbs sont respectivement :

\[\begin{aligned} H^m&=H_0^m+\int C_p~dT\\ S^m&=S_0^m+\int\frac{C_p}{T}~dT-R~\ln(p)\\ G^m&=H_0^m+\int C_p~dT-T\int\frac{C_p}{T}~dT-T~S_0^m+R~T~\ln(p)\end{aligned}\]

On remarque en intégrant par parties que :

\[\begin{aligned} \int\frac{1}{T}~C_p~dT&=\frac{1}{T}\int C_p~dT-\int\Big\{-\frac{1}{T^2}\int C_p~dT\Big\}~dT\\ \int C_p~dT&=T\int\frac{C_p}{T}~dT=-T\int\frac{\int C_p~dT}{T^2}~dT\end{aligned}\]

On en tire : \[G^m=H_0^m-T\int\frac{\int C_p~dT}{T^2}~dT-T~S_0^m+R~T~\ln(p)\]

Posons : \[\Phi=\frac{H_0^m}{R~T}+\frac{1}{R}\int\frac{\int C_p~dT}{T^2}~dT\qquad\text{fonction de T seulement}\]

Il vient alors : \[G^m=R~T~\{\Phi+\ln(p)\}\]

9. Fonction de Gibbs et mélange de gaz parfaits non réagissants

Le mélange contient \(n_i\) moles de gaz parfait \(G_i\), etc. Nous pouvons définir l’enthalpie partielle et la fonction de Gibbs partielle du gaz \(G_i\) comme étant égales à l’enthalpie et à la fonction de Gibbs du gaz \(G_i\) lorsqu’il occupe tout seul à la température \(T\) tout le volume du mélange.

Si nous opérons alors sur le mélange comme précédemment de façon réversible, il est clair que l’enthalpie totale ne change pas (\(U\) et \(p~v\) constants) et que par suite la fonction de Gibbs est la somme des fonctions de Gibbs partielles des divers gaz parfaits constituants. On a donc : \[G_{mel}=R~T~\sum_i\{\Phi_i+\ln(p_i)\}=R~T~\sum_i\{\Phi_i+\ln(p)+\ln(x_i)\}\]

Avec : \[\Phi=\frac{H_{0i}^m}{R~T}-\frac{1}{R}\int\frac{\int C_{pi}~dT}{T^2}~dT-\frac{S_{oi}^m}{R}\qquad\text{fonction de T seulement}\]

Le mélange à \(T\) et \(p\) constants s’accompagne donc comme il se doit d’une diminution d’une diminution de la fonction de Gibbs : \[\Delta G=R~T~\sum_i n_i~\ln(x_i)\]

Ces diverses expressions nous seront d’un grand secours dans l’étude de l’équilibre physicochimique.