1. Mélange liquide – vapeur

Nous nous proposons d’étudier ici un peu plus en détail l’équilibre entre phases liquide et vapeur d’une substance pure, équilibre dont l’importance pratique est considérable (machines à vapeur, turbines).

1.1. Pression de vapeur saturante

Nous savons déjà qu’à chaque température inférieure à la température critique correspond une pression déterminée où le liquide et la vapeur sont en équilibre. Cette pression de vapeur saturante \(P\) varie avec la température \(T\). Sa variation peut être représentée par une courbe que l’on peut prolonger jusqu’au zéro absolu par suite des possibilités de surfusion du liquide.

Quand \(T\) tend vers 0, \(P\) tend aussi vers 0. La vapeur se rapproche donc des propriétés du gaz parfait. Son volume spécifique étant \(u'\), on aura : \[u'\rightarrow\infty\quad\text{entrainera}\quad\frac{P}{T}\approx\frac{r}{u'}\rightarrow 0\]

La courbe part donc de l’origine tangentiellement à l’axe des températures. Elle s’arrête au point critique sans y présenter de particularités : quand \(T\) se rapproche de \(T_c\), \(\cfrac{dP}{dT}\) et \(\cfrac{d^2P}{dT^2}\) ne tendent ni vers zéro ni vers l’infini.

On peut le vérifier par exemple en supposant que le fluide satisfait à l’équation de Van der Waals. En affectant de l’indice \(l\) les quantités relatives au liquide, on a : \[dP=\Big(\frac{\partial P_l}{\partial T}\Big)_v~dT+\Big(\frac{\partial P_l}{\partial v}\Big)_T~du\]

\(dP/dT\) est un infiniment petit de l’ordre de \(du\) pour \(T\approx T_c\) (sommet de la courbe de saturation), mais \(\Big(\cfrac{\partial P}{\partial v}\Big)_T\) est un infiniment petit du second ordre par rapport à \(du\) (tangente horizontale d’inflexion pour l’isotherme critique). Nous pouvons donc écrire au point critique, avec une erreur négligeable : \[\frac{dP}{dT}\approxeq \Big(\frac{\partial P_l}{\partial T}\Big)_v =r~(v_c-b)\approx\frac{r}{2~b}=4~\frac{P_c}{T_c}\]

Cette égalité ne donne évidemment qu’un ordre de grandeur pour les gaz réels, mais elle suffit à montrer que la courbe des tensions de vapeur ne présente pas de singularité au point critique.

1.2. Pression de vapeur loin du point critique

Nous avons vu que l’on peut écrire, la vapeur étant assimilable à un gaz parfait et en désignant par \(L\) la chaleur latente de vaporisation : \[\frac{d[\ln(P)]}{dT}=\frac{M~L}{R~T^2}\]

Nous avions d’autre part déduit du premier principe, \(C_p\) et \(C'_p\) étant les capacités calorifiques moléculaires à pression constante du liquide et de la vapeur : \[M~\frac{dL}{dT}=C'_p-C_p\]

On pourra toujours, dans un domaine de températures qui ne soit pas trop étendu, supposer à peu près constantes les chaleurs spécifiques et écrire :

\[\begin{aligned} M~L&=R~(\gamma~T+\beta)\\ \text{avec :}\qquad C'_p-C_p&=R~\gamma\qquad\qquad\gamma,~\beta~\text{ constantes}\end{aligned}\]

Soit encore :

\[\begin{aligned} \frac{d[\ln(P)]}{dT}&=\frac{\gamma}{T}+\frac{\beta}{T^2}\\ \text{C'est-à-dire :}\qquad \ln(P)&=\alpha-\frac{\beta}{T}+\gamma~\ln(T)\end{aligned}\]

Cette formule, dite formule de Dupré, s’applique particulièrement bien au voisinage du zéro absolu où la vapeur est très voisine d’un gaz parfait.

La chaleur spécifique moléculaire vaut alors : \(C'_p=\cfrac{5~R}{2} \), les gaz se comportant à très basse température comme des gaz monoatomiques.

Quant à \(C_p\), elle est sensiblement nulle ; on a donc \(\gamma=\cfrac{5}{2}\) et \(\beta=\cfrac{ML_0}{2}\), \(L_0\) étant la chaleur de vaporisation au zéro absolu. On a alors : \[\ln(P)=\frac{5}{2}~\ln(T)-\frac{M~L_0}{R~T}+\alpha\]

Cette formule peut être utilisée pour calculer la pression de vapeur à des températures où elle est trop basse pour pouvoir être mesurée.

La valeur de \(L_0\) peut être obtenue à partir de mesures de \(L\) à température plus élevée, connaissant la loi de variation avec \(T\) de \(C_p\) et \(C'_p\) ; il suffit de mesurer \(P\) à une température où la pression de vapeur est notable pour obtenir la valeur de la constante \(\alpha\).

Une formule tout à fait analogue est bien entendu valable pour la pression de sublimation d’un solide, à température assez basse pour que la vapeur soit assimilable à un gaz parfait.

Exercice

Nous allons à titre d’exercice établir cette formule par la mécanique statistique, dans le cas d’un solide monoatomique (mercure par exemple) et obtenir du même coup la valeur de la constante \(\alpha\).

Nous allons dans ce but calculer la valeur absolue de l’entropie du gaz parfait monoatomique que constitue une mole de vapeur, le zéro des entropies étant fourni par le solide (cristal parfait) au zéro absolu.

Bien entendu, il se peut que la structure interne des atomes introduise une cause de désordre mais nous n’avons pas à en tenir compte puisqu’elle se retrouve identique dans le solide et la vapeur et que nous cherchons à calculer la variation d’entropie qui accompagne la sublimation.

Connaissant l’expression \(S_v\) de l’entropie par mole de la vapeur et sachant que l’entropie par mole du solide est : \[S_{sol}=\int_0^T\frac{C_p^{sol}}{T}~dT\]

\(C_p^{sol}\) étant la chaleur spécifique à pression constante du solide qui est sensiblement nulle au voisinage du zéro absolu.

Nous écrirons : \[S_v-S_{sol}=\frac{ML}{T}\qquad\ M\text{ : masse moléculaire}\]

Avec : \[M~L=M~L_0+\int_0^T(C_p^v-C_p^{sol})~dT=M~L_0+\frac{5}{2}~R~T-\int_0^T C_p^{sol}~dT\]

Soit encore : \[S_v=\frac{M~L_0}{T}+\frac{5~R}{2}+\int_0^T \frac{C_p^{sol}}{dT}~dT-\frac{1}{T}\int_0^T C_p^{sol}~dT\]

Il nous suffit donc de connaître l’expression de \(S_v\) en fonction de \(P\) (pression de vapeur) et de \(T\) pour obtenir l’expression de la pression de vapeur \(P\) du solide en fonction de quantités connues.

– Calcul de \(S_v\) par la mécanique statistique

Nous partons de l’expression \(S=k~\ln(W)\) (voir plus haut) : \[\ln(W)=\sum_{i=1}^c \Big\{\frac{N_i}{g_i}~\ln\frac{N_i+g_i}{N_i}+\ln\frac{N_i+g_i}{g_i}\Big\} \qquad \text{(sommation sur les cellules)}\]

La condition d’équilibre s’écrit : \[\ln\frac{N_i+g_i}{N_i}=\alpha+\beta~U_i\]

D’autre part : \[g_i\gg N_i\quad\Rightarrow\quad \ln\Big(1+\frac{N_i}{g_i}\Big)\approx\frac{N_i}{g_i}=\overline{n_i}\]

On a donc : \[\ln(W)=\sum_{i=1}^c\overline{n_i}~(\alpha+\beta~U_i+1)=(\alpha+1)~N+\frac{U}{k~T}\]

Or, \(U=3~R~T/2\) (gaz monoatomique). En définitive : \[S_v=k~\ln(W)=R~(\alpha+1)+\frac{3}{2}~R=R~\Big(\alpha+\frac{5}{2}\Big)\]

La constante \(\alpha\) est celle qui figure dans la distribution de Boltzmann (ne pas confondre avec la constante introduite plus haut dans la formule de Dupré). On la calcule en exprimant que le nombre total des molécules est égal à \(N\). Nous l’obtiendrons immédiatement en cherchant le nombre de molécules dans une cellule de volume de l’extension en phase.

Rappelons la distribution de Maxwell :

\[\begin{aligned} &dn=\frac{N}{V}~\Big(\frac{m}{2~\pi~k~T}\Big)^{3/2}~\exp(-U/k~T)~dx~dy~dz~dv_x~dv_y~dv_z\\ \text{ou encore}\\ &dn=\frac{N}{V}~(m~2~\pi~kT)^{-3/2}~\exp(-U/k~T)~dx~dy~dz~dp_x~dp_y~dp_z\end{aligned}\]

Nous obtenons pour la cellule de volume \(h^3\) dans l’espace \((x~,p)\) : \[\overline{n_i}=\frac{N~h^3}{V}~(m~2~\pi~k~T)^{-3/2}~\exp(-U_i/k~T)=\exp(-\alpha-U_i/k~T)\]

Soit : \[e^{\alpha}=\frac{V}{N}~\Big(\frac{2~\pi~m~k~T}{h^2}\Big)^{3/2}\]

Ou encore : \[\alpha=\frac{3}{2}~\ln\frac{2~\pi~m}{h^2}+\frac{3}{2}~\ln(R~T)+\ln(V)-\frac{5}{2}~\ln(N)\]

Et enfin, en remarquant que \(P~V=R~T\) : \[\frac{S_v}{R}=\alpha+\frac{5}{2}=-\ln(P)+\frac{5}{2}~[1+\ln(k)]+\frac{3}{2}~\ln\frac{2~\pi~m}{h^2}+\frac{5}{2}~\ln(T)\]

C’est la formule de Sackur-Tetrode.

Remarquons en passant que nous obtenons bien une expression du type : \[S=S_0+C_p~\ln(T)-R~\ln(P)\]

la constante \(S_0\) étant ici parfaitement déterminée.

Nous en tirons la formule de pression de vapeur : \[\ln(P)=\frac{5}{2}\ln(T)-\frac{S_v}{R}+\frac{5}{2}~[1+\ln(k)]+\frac{3}{2}~\ln\frac{2~\pi~m}{h^2}\]

Soit, en remplaçant \(S_v\) par l’expression vue plus haut : \[\ln(P)=\frac{5}{2}~\ln(T)-\frac{M~L_0}{R~T}+\alpha'\]

Avec : \[\alpha'=\frac{5}{2}~\ln(k)+\frac{3}{2}~\ln\frac{2~\pi~m}{h^2}+\frac{1}{R}~\Big\{\frac{1}{T}\int_0^T C_p^{sol}~dT-\int_0^T\frac{C_p^{sol}}{T}~dT \Big\}\]

Aux températures voisines du zéro absolu, le dernier membre entre accolades est sensiblement nulle et \(\alpha'\) se réduit à la constante des pressions de vapeur : \[\alpha^0=\frac{5}{2}~\ln(k)+\frac{3}{2}~\ln\frac{2~\pi~m}{h^2}\]

Nous en retiendrons principalement que la mesure des pressions de vapeur permet une détermination de la constante de Planck \(h\) et fournit une vérification expérimentale du principe de Heisenberg qui nous a permis de fixer à \(h^3\) le volume des cellules élémentaires de l’extension en phase.

1.3. Pression de vapeur et équation d’état

La pression de vapeur peut théoriquement être déduite de l’équation d’état qui lie les états homogènes du fluide.

Supposons par exemple que le fluide satisfasse à l’équations de Van der Waals. Il s’agit de placer le palier de vaporisation sur l’isotherme théorique \((T<T_c)\) qui présente un minimum et un maximum.

Pour tout état homogène du fluide, l’énergie interne, la température et l’entropie peuvent être exprimées en fonction de \(p\) et \(v\) (une fois choisies les constantes additives de \(U\) et \(S\)). La fonction de Gibbs \(G\) peut donc être exprimée en fonction de \(p\) et \(v\).

Il suffit d’écrire alors \(G(A')=G(A)\) pour placer sans ambigüité le palier \(AA'\) sur l’isotherme. Nous pouvons par exemple écrire : \[\int_{AA'} dG=\int_{AA'}(v~dp-S~dT)=0\]

L’intégrale curviligne étant calculée sur une courbe quelconque partant de \(A\) pour aboutir à \(A'\).

Cette courbe n’est nullement astreinte à passer uniquement par des points du plan correspondant à des états d’équilibre physiquement réalisable du fluide. On pourrait la faire passer par des points où \(v\) est négatif sans inconvénient.

Nous choisirons tout simplement comme courbe l’isotherme de van der Waals sur lequel \(T = cte\). Il suffit en effet d’intégrer la fonction \(G(p,v)\), fonction mathématique qui n’a pas besoin en cours de route de représenter la fonction de Gibbs d’un fluide expérimentalement défini.

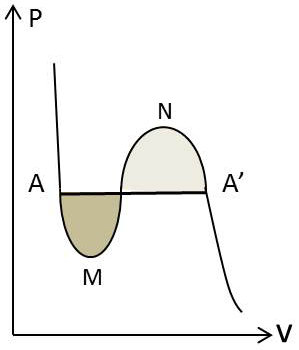
En prenant l’intégrale le long de la courbe \(AMNA'\), nous aurons alors la condition : \[\int_{AA'} v~dp=0\]

Cela signifie que les aires hachurées sur la figure doivent être égales : le problème se ramènera donc à placer le palier \(AA'\) de telle façon que cette condition soit remplie.

Remarque

Ce théorème dû à Maxwell peut se démontrer très simplement en faisant directement appel au second principe.

Supposons que nous fassions décrire au fluide le cycle isotherme et réversible \(AMNA'A\) : il a reçu au total un travail nul d’où l’égalité des aires. On suppose toutefois ainsi décrite de façon réversible une succession \((MN)\) d’états déséquilibre instables, ce qui est physiquement impossible, et il vaut lieux éviter de fonder des raisonnements sur des expériences qui ne sont pas au moins réalisables de façon approximative.

1.4. Chaleur latente de vaporisation

Nous savons que la valeur de la chaleur latente de vaporisation est donnée par la formule de Clapeyon : \[L=T~(u'-u)~\frac{dP}{dT}\]

Loin du point critique, nous avons vu que l’on peut écrire : \[L=\frac{R~T^2}{M}~\frac{d[\ln(p)]}{dT}\]

Cherchons ce que devient la chaleur latente de vaporisation au voisinage du point critique. Il est évident qu’elle va s’annuler au point critique, le fluide s’y confondant avec la vapeur. Passons à la dérivée ; nous pouvons écrire : \[\frac{dL}{dT}=(u'-u)~\frac{dP}{dT}+T~(u'-u)~\frac{d^2P}{dT^2}+T~\frac{dP}{dT}~\Big(\frac{du'}{dT}-\frac{du}{dT}\Big)\]

Les deux premiers termes sont nuls au point critique où \(u'=u\) , les deux dérivées \(dP/dT\) et \(d^2P/dT^2\) n’étant pas définies.

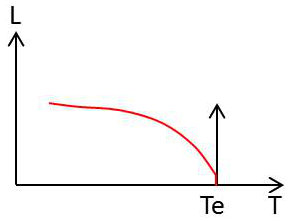Par ailleurs, \(du'/dP\rightarrow -\infty\) et \(du/dP\rightarrow +\infty \) au point critique (sommet de la courbe de saturation) et il en est de même pour \(du'/dT\) et \(du/dT\) puisque \(dP/dT\neq 0\). Donc, au point critique, \(dL/dT\rightarrow -\infty\). La courbe de variation de la chaleur latente \(L\) a l’allure représentée sur la figure ci-contre.

2. Étude du mélange liquide - vapeur

Nous supposerons égale à l’unité la masse totale de la substance. Le mélange est défini par sa température \(T\), sa pression \(P\) qui ne dépend que de \(T\), de son titre \(x\) en vapeur (qui est tout simplement ici la masse de la vapeur puisque la masse totale est égale à l’unité).

Dans le diagramme de Clapeyron, le mélange liquide - vapeur est représenté par un point \(P\) situé sur le palier d’ordonnée \(P\) et qui partage ce palier \(AA'\) dans le rapport \(x/(1-x)\)  ; on a donc \(AM/AA'=x\) (voir figure § 1.3)

2.1. Chaleurs spécifiques le long de la courbe de saturation

Soit \(dQ\) la quantité de chaleur qu’il faut fournir au liquide de saturation pour élever sa température de \(dT\) en le maintenant à l’état de liquide de saturation (le point figuratif dans le diagramme de Clapeyron restant donc sur la branche liquide de la courbe de saturation).

Nous poserons : \[dQ=m~dT\]

et donnerons à \(m\) le nom de chaleur spécifique du liquide le long de la courbe de saturation à la température \(T\).

De même, si \(dQ'\) est la chaleur nécessaire pour élever de \(dT\) la température de la vapeur saturante, nous poserons : \[dQ'=m'~dT\]

et donnerons à \(m'\) le nom de chaleur spécifique de la vapeur le long de la courbe de saturation à la température \(T\).

Évaluons les chaleurs spécifiques \(m\) et \(m'\).

Nous désignerons par des lettres ordinaires les quantités relatives au liquide (en dehors de la courbe de saturation) et par des lettres primées les quantités relatives à la vapeur sèche, par \(u\) et \(u'\) les volumes spécifiques du liquide de saturation et de la vapeur saturante.

Nous pouvons écrire :

\[\begin{aligned} dQ&=c_v~dT+l~du=c_p~dT+h~dP\\ dQ'&=c'_v~dT+l'~du'=c'_p~dT+h'~dP\end{aligned}\]

soit, en appliquant des formules connues :

\[\begin{aligned} m&=\frac{dQ}{dI}=c_v+T~\Big(\frac{\partial P}{\partial T}\Big)_v~\frac{du}{dT} =c_p-T~\Big(\frac{\partial v}{\partial T}\Big)_p~\frac{dP}{dT}\\ m'&=\frac{dQ'}{dI}=c'_v+T~\Big(\frac{\partial P'}{\partial T}\Big)_v~\frac{du'}{dT} =c'_p-T~\Big(\frac{\partial v'}{\partial T}\Big)_p~\frac{dP}{dT}\end{aligned}\]

\(c_v\) et \(c'_v\) sont respectivement égaux à \(\partial U/\partial T\) et \(\partial U'/\partial T\) et ne sont ni nuls ni infinis au point critique, l’augmentation d’énergie à volume constant ayant lieu par simple accroissement de l’agitation moléculaire qui ne présente au point critique aucune singularité.

Or, \(dU/dT\rightarrow +\infty\) et \(dU'/dT\rightarrow -\infty\) quand \(T\rightarrow T_c\). Nous voyons donc que \(m\rightarrow +\infty\) et \(m'\rightarrow -\infty\) quand \(T\rightarrow T_c\).

Plaçons-nous maintenant loin du point critique. Le liquide étant très peu dilatable, \((\partial v/\partial T)_p\) est petit et \(m\) est très voisin de \(c_p\). Par contre, \((\partial v'/\partial T)_p\) est important et \(m'\) aura en général une valeur négative.

Ceci peut sembler curieux ; mais il faut remarquer que \(m'\) comprend deux termes : le premier est \(c'\) qui correspond à l’agitation thermique et est nécessairement positif ; le second est \(l'~du'\) qui correspond à la chaleur absorbée par la vapeur dans la compression isotherme nécessaire pour la ramener à l’état de vapeur saturante, bien qu’on ait un peu élevé la température.

La compression isotherme dégage de la chaleur et \(l'~du'\) est négatif et généralement plus grand en valeur absolue que \(c'_v~dT\). On est en tout cas assuré que \(m'\) sera négatif à toute température pour laquelle l’isotherme de la vapeur sèche confond presque avec la courbe de saturation, c’est à dire au voisinage de \(T_c\) et pour les températures très basses.

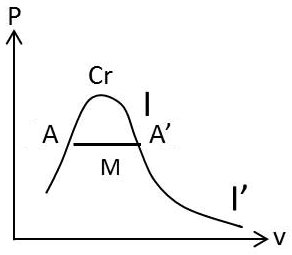Aux températures intermédiaires, il pourra arriver que, dans toute une région de températures, \(m'\) soit positif. Il existe alors deux températures d’inversion de \(m'\) auxquelles correspondent deux points d’inversion \(I\) et \(I'\). Alors \(m'\) est positive dans tout l’intervalle de températures compris entre les températures des points d’inversion, négative à l’extérieur de cet intervalle.

Seules les substances à molécules relativement complexes (benzène, éther) présentent des points d’inversion.

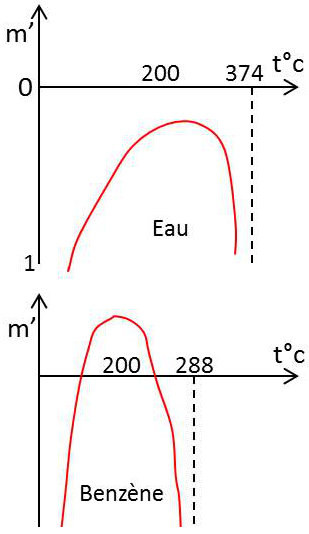Pour l’eau par exemple, \(m'\) est toujours négative et il n’y a pas de point d’inversion. Les variations de la chaleur spécifique \(m'\) avec la température pour la vapeur d’eau et pour la vapeur de benzène sont indiquées ci-contre.

À basse température, nous avons déjà remarqué que \(m\) est voisine de la chaleur spécifique à pression constante du liquide. Quant à \(m'\), nous pouvons écrire, en assimilant la vapeur à un gaz parfait : \[m'=c'_p-T~\Big(\frac{\partial v'}{\partial T}\Big)_p~\frac{dP}{dT}=c'_p-\Big(\frac{R~T}{M~P}\Big)~\frac{dP}{dT}\]

Comparant à la formule de Clapeyron qui s’écrit dans ces conditions : \[L=\Big(\frac{R~T^2}{M~P}\Big)~\frac{dP}{dT}\]

il vient : \[m'=c'_p-\frac{L}{T}\]

loin du point critique quand \(T\rightarrow 0\), \(L\rightarrow L_0\neq 0\) et par suite \(m'\rightarrow -\infty\).

Nous verrons un peu plus loin une expression très simple liant à toute température la différence \((m’-m)\) à la chaleur latente de vaporisation \(L\).

2.2. Énergie interne et entropie d’un mélange liquide-vapeur

Étudions tout d’abord le mélange de titre \(x=0\), c’est-à-dire le liquide de saturation. Il est clair que pour toute modification infinitésimale de température le long de la branche liquide de la courbe de saturation :

\[\begin{aligned} dU&=m~dT-p~du\\ dS&=\frac{m}{T}~dT\end{aligned}\]

Convenons de choisir pour origine des énergies internes et des entropies les valeurs de \(U\) et de \(S\) lorsque la substance est à l’état liquide dans les conditions \((T_0,~P_0,~u_0)\) du point triple solide - liquide - vapeur. Il vient alors :

\[\begin{aligned} U&=\int_{T_0}^T m~dT-\int_{u_0}^u p~du\\ S&=\int_{T_0}^T \frac{m}{T}~dT\end{aligned}\]

Dans un intervalle de températures qui ne soit pas trop étendu au-dessus de \(T_0\) et reste loin du point critique, nous pourrons négliger les variations de \(u\) et considérer \(m\) comme constante. Il vient alors :

\[\begin{aligned} U&=m~(T-T_0)\\ S&=m~\ln\frac{T}{T_0}\end{aligned}\]

Pour l’eau par exemple, \(T_0\) = 273 K et nous pourrons écrire, tant que \(t\) (en °C) reste très inférieur à 300 °C (\(t_c\)=374 °C) :

\[\begin{aligned} U&=m~t\\ S&=m~\ln\Big(1+\frac{t}{273}\Big)\end{aligned}\]

avec : \(m=1,02~J/K=0,24~cal/K\).

Passons maintenant à un mélange liquide - vapeur de titre \(x\). Ce mélange peut être obtenu à partir du liquide de saturation pris à la même température et à la même pression par absorption d’une quantité de chaleur \([x~L]\) et d’un travail \([-x~P~(u'-u)]\).

On a donc, pour un mélange de titre \(x\) et de masse unité :

\[\begin{aligned} U_x&=\int_{T_0}^T m~dT-\int_{u_0}^u P~du+x~[L-P~(u'-u)]\\ S_x&=\int_{T_0}^T\frac{m}{T}~dT+x~\frac{L}{T}\end{aligned}\]

En particulier, pour \(x=1\) (vapeur saturante), il vient :

\[\begin{aligned} U'&=\int_{T_0}^T m~dT-\int_{u_0}^u P~du+L-P~(u'-u)\\ S'&=\int_{T_0}^T\frac{m}{T}~dT+\frac{L}{T}\end{aligned}\]

Tant que l’on reste loin du point critique, on pourra se contenter des approximations :

\[\begin{aligned} U_x&=m~(T-T_0)+x~[L-P~(u'-u)]\\ S_x&=m~\ln\frac{T}{T_0}+x~\frac{L}{T}\end{aligned}\]

Formule très utilisée dans les calculs relatifs à la vapeur d’eau loin du point critique (machines à vapeur conventionnelles).

\((T-T_0)\) est la température centigrade et des tables fournissent aux diverses températures la quantité \([L-P~(u'-u)]\) qui ne dépend évidemment que de \(T\).

Expression de \((m’-m)\)

Échauffons de \(dT\) l’unité de masse de vapeur en la maintenant saturante. Sa variation d’entropie est : \[dS'=m~\frac{dT}{T}+d\Big(\frac{L}{T}\Big)=m'~\frac{dT}{T}\]

puisque la chaleur absorbée de façon réversible est \(m'~dT\) .

On en tire : \[\frac{m'-m}{T}=\frac{d(L/T)}{dT}=\frac{1}{T}~\frac{dL}{dT}-\frac{L}{T^2}\]

Soit : \[m'-m=\frac{dL}{dT}-\frac{L}{T}\qquad\text{à toute température.}\]

formule très importante qui permet de calculer \(m'\) à toute température éloignée de la température critique connaissant la variation de \(L\) avec \(T\) (formule empirique par exemple) en assimilant \(m\) à la chaleur spécifique à pression constante du liquide.

Pour l’eau, par exemple, loin du point critique, on peut utiliser la formule de Regnault : \[L=796-0,695~T\qquad\text{(en calories)}\]

d’où l’on tire, en posant \(m=1,02\) et en exprimant toutes les chaleurs en calories : \[m'=1-\frac{796}{T}\qquad\text{(loin du point critique)}\]

2.3. Détente adiabatique et réversible d’un mélange liquide - vapeur

L’entropie reste constante. L’équation d’une détente adiabatique et réversible est donc : \[\int_{T_0}^T m~\frac{dT}{T}+x~\frac{L}{T}=\text{constante}\]

Le titre \(x\) varie au cours de la détente. L’équation ne reste évidemment valable que tant qu’elle fournit des valeurs \(0<x<1\). Dès que \(x>1\) on remplacera l’équation par celle de l’adiabatique de la vapeur sèche. Nous verrons que \(x\) ne devient jamais nul dans une détente adiabatique.

Supposons que la température de début de détente soit très inférieure à \(T_c\). Nous pourrons alors poser : \[S=m~\ln\frac{T}{T_0}+x~\frac{L}{T}\]

soit pour l’équation de la détente isentropique : \[m~\ln\frac{T}{T_0}+x~\frac{L}{T}=cte\]

– Premier cas

La détente est définie par les températures initiale et finale. Soient \(T_i,~T_f,~x_i\) ces températures et le titre initial. Le titre en fin de détente est fourni par : \[m~\ln\frac{T_i}{T_0}+x_i~\frac{L(T_i)}{T_i}=m~\ln\frac{T_f}{T_0}+x_f~\frac{L(T_f)}{T_f}\]

Soit encore : \[x_f=\frac{T_f}{L_f}~\Big\{m~\ln\frac{T_i}{T_0}+x_i~\frac{L_i}{T_i}\Big\}\]

La détente abaisse nécessairement la température (si elle s’élevait, elle élèverait \(P\) et le mélange liquide-vapeur serait en équilibre instable). Le titre est donc toujours positif et l’on ne saurait obtenir du liquide exempt de vapeur par détente adiabatique du mélange.

Le cas où la détente serait définie par les pressions de départ et d’arrivée se ramène évidemment au premier, les températures initiale et finale s’obtenant immédiatement à partir de la courbe des pressions de vapeur.

– Deuxième cas

La détente est définie par les volumes initial et final. C’est là le cas usuel que l’on rencontre par exemple dans les calculs relatifs à la machine à vapeur. Supposons donc que nous connaissions \(T_i,~v_i,~v_f\). On en déduit immédiatement : \[x_i=\frac{v_i-u_i}{u'_i-u_i}\]

\(u_i,~u'_i\) étant fournis par les tables de constantes en fonction de \(T_i\). Les tables fournissent également \(L_i\).

On procède alors par tâtonnements. On essaie une température vraisemblable en fin de détente \(T_1\) à laquelle correspondraient d’après les tables des volumes spécifiques liquide et vapeur \(u_1,u'_1\).

On calcule le titre \(x_1\) du mélange lorsqu’il atteint la température \(T_1\) ; on en déduit le volume : \[v_1=u_1+x_1~(u'_1-u_1)\]

que l’on compare à \(v_f\).

Si par exemple \(v_1<v_f\), on recommence le tout pour une température \(T_2\) un peu plus basse, et ainsi de suite jusqu’à ce que l’on ait encadré \(v_f\) entre deux valeurs successives. On obtient alors par interpolation des valeurs approchées de \(T_f\) et \(x_f\) (on peut aussi tracer une portion de courbe donnant \(v_f\) en fonction de \(T_f\)).

2.4. Travail fourni par le mélange liquide-vapeur dans la détente isentropique

Le travail fourni par le mélange liquide-vapeur dans la détente isentropique est évidemment égal à la diminution d’énergie interne du mélange : \[W=-\Delta U=U_i-U_f\]

En supposant que la température de départ est très inférieure à la température critique, nous pourrons écrire : \[W=m~(T_i-T_f)+x_i~[L_i-P_i~(u'_i-u_i)]-x_f~[L_f-P_f~(u'_f-u_f)]\]

La quantité \([L-P~(u'-u)]\) est donnée par les tables dans le cas de l’eau ; connaissant \(T_f\) et par suite \(x_f\), on calcule aisément \(W\).

Formule de Rankine

Dans le cas de la vapeur d’eau saturante se détendant de façon isentropique à partir d’une température inférieure à 200 °C, on obtient une très bonne approximation en appliquant au mélange liquide - vapeur, une formule empirique, la formule de Rankine (de forme analogue à celle de la formule de Laplace pour les gaz parfaits) : \[P~v^n=cte\quad;\quad n=1,114\]

La connaissance du rapport \(v_f/v_i\) (rapport de détente) fournit alors immédiatement \(P_f\) et par suite \(T_f\), d’où le titre \(x_f\) en fin de détente. En outre, le travail \(W\) fourni par la vapeur s’écrit simplement : \[W=\frac{P_i~v_i-P_f~v_f}{n-1}\]

2.5. Représentations graphiques

Nous avons vu comment un mélange liquide - vapeur pouvait être représenté par un point dans le diagramme de Clapeyron. Il est souvent pus judicieux d’utiliser d’autres coordonnées pour représenter l’état du fluide.

2.5.1. Diagramme entropique

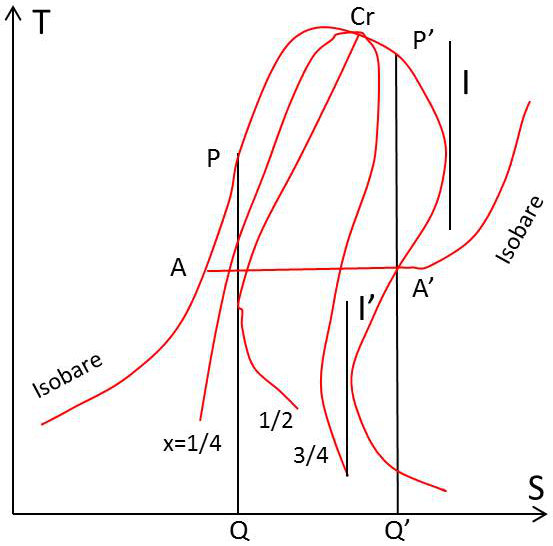On porte en abscisse l’entropie et en ordonnée la température. Les paliers de vaporisation sont des segments horizontaux \((T=cte)\).

La courbe de saturation a une pente constamment positive sur la branche liquide. En effet, \(dT/dS\) y est égal à \(T:m\), toujours positif.

Si la substance ne présente pas de points d’inversion, la branche vapeur a une pente toujours négative \((m'<0)\).

Si, par contre, la substance présente des points d’inversion, la pente de la courbe d’inversion est infinie (tangente verticale) en \(I\) et \(I'\) et positive entre \(I\) et \(I'\).

On vérifie immédiatement qu’un mélange de titre \(x\) est représenté par un point qui partage le palier de vaporisation dans le rapport \(x/(1-x)\) comme c’était le cas pour le diagramme de Clapeyron.

On peut tracer à l’intérieur de la courbe de saturation les courbes de titre constant. Elles ont toutes au point critique une tangente horizontale, sauf la courbe qui coupe la courbe de saturation sous un angle nul.

Remarquons en outre que les isobares de la vapeur \((p = cte)\) ont une pente d’autant plus accentuée que la température est plus forte.

On a en effet : \[\Big(\frac{\partial S}{\partial T}\Big)_p=\frac{C'_p}{T} \qquad\text{soit :}\quad \Big(\frac{\partial T}{\partial S}\Big)_p=\frac{T}{C'_p}\]

Aux pressions assez faibles pour que la vapeur sèche puisse être assimilée à un gaz parfait,\(C_p\) ne dépend que de \(T\) et les isobares se déduisent l’une de l’autre par translation horizontale. En outre, \(C'_p\) croît beaucoup moins vite que \(T\) aux températures usuelles et les isobares tournent leur concavité vers le haut. Du côté liquide et loin du point critique, les isobares se confondent pratiquement avec la courbe de saturation \((m\approx C_p)\).

Dans le diagramme entropique, l’aire \(T.dS\) comprise en-dessous d’une courbe représentant une transformation réversible \(I\rightarrow F\) représente la chaleur reçue par le système au cours de la transformation, mais il est indispensable pour cela que la transformation soit réversible. Pour un cycle réversible, la chaleur reçue est mesurée par l’aire du cycle, affectée du signe \((+)\) si le cycle est parcouru dans le sens rétrograde (sens de rotation des aiguilles d’une montre).

Un cycle de Carnot est représenté par un rectangle dans le diagramme entropique.

2.5.2. Diagramme de Mollier

On porte en abscisse l’entropie et en ordonnée l’enthalpie. La relation : \[dH=v~dP+T~dS\]

valable aussi bien pour le mélange liquide - vapeur que pour le fluide homogène, indique que la pente \(dH/dS\) d’une isobare est égale à la température thermodynamique.

Les paliers de vaporisation sont donc là encore rectilignes, mais leur pente croît à mesure que l’on se rapproche du point critique.

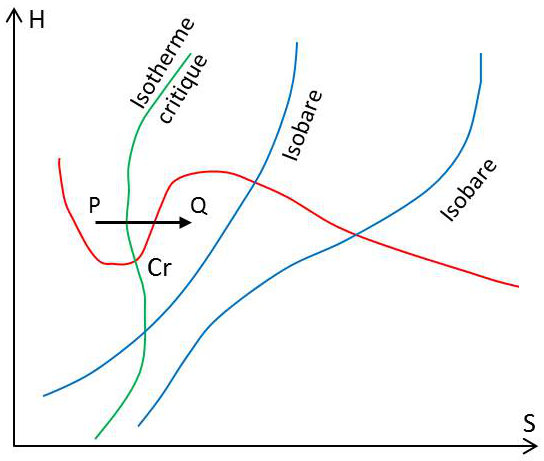Ce diagramme est très commode pour représenter les transformations qui se produisent dans une machine à vapeur.

Une détente adiabatique réversible est représentée par une verticale descendante. Par contre, une détente adiabatique Joule-Kelvin (détente freinée ou laminée) est représentée par une horizontale se dirigeant vers la droite (\(H\) constante, \(S\) croissante).

Or, la détente de la vapeur dans le cylindre peut être assimilée à une détente isentropique, alors que la détente que subit la vapeur par perte de charge lorsqu’elle circule dans des canalisations étroites est approximativement une détente de Joule-Kelvin.

2.6. Étude graphique des détentes adiabatiques

Étudions la détente isentropique sur le diagramme entropique \((T,S\)) où elle est représentée par une verticale descendante. On voit immédiatement sur le diagramme que la détente isentropique du liquide de saturation entraîne toujours une vaporisation partielle. La verticale coupe des courbes \(x=cte\) de titre de plus en plus élevé, jusqu’à ce qu’elle soit tangente à l’une de ces courbes ; une détente ultérieure provoque une condensation partielle.

Étudions maintenant la détente isentropique de la vapeur saturante, en supposant tout d’abord que \(m'\) est négative (pas de points d’inversion). La détente entraîne toujours au début une condensation partielle ; il peut arriver qu’ensuite ait lieu une faible vaporisation, puis la condensation reprend.

La détente isentropique d’une vapeur saturante présentant deux points d’inversion \(I\) et \(I'\) entraîne des phénomènes plus compliqués que le diagramme met immédiatement en évidence. Partant par exemple du point \(P'\), la détente entraîne successivement une condensation partielle, puis une vaporisation totale, une surchauffe de la vapeur sèche (le mot surchauffe étant peut-être mal choisi puisque c’est en se refroidissant que la vapeur subit cette surchauffe), enfin une condensation de plus en plus poussée.

Si la détente adiabatique est irréversible, la courbe qui la représente (approximativement puisqu’en fait une détente irréversible n’est pas représentable par une courbe bien définie) a une pente négative. On en déduit immédiatement que la détente irréversible entraîne, à variation de température égale, une condensation plus faible, ou une vaporisation plus importante, ou une plus grande surchauffe, que la détente isentropique.

C’est par exemple le cas de la détente Joule Kelvin représentable sur le diagramme de Mollier par une horizontale se dirigeant vers la droite. Nous voyons immédiatement sur la figure que l’on ne pourra obtenir la liquéfaction d’un gaz par détente Joule-Kelvin que si les conditions initiales sont voisines des conditions critiques \((P,~Q)\).

3. Machines à vapeur

3.1. Description du fonctionnement

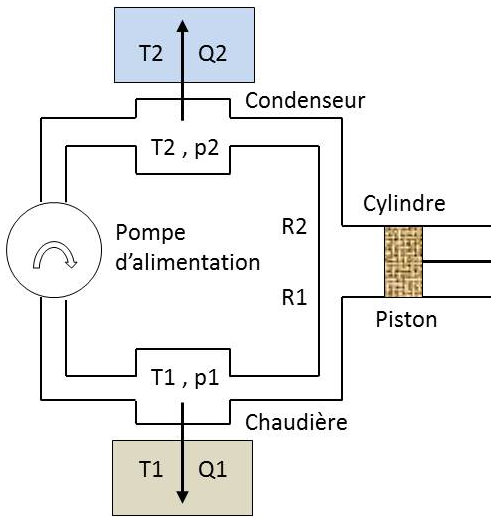À titre d’application des résultats que nous venons d’obtenir, étudions sommairement les conditions de fonctionnement d’une machine à vapeur classique. Les organes principaux sont représentés sur la figure ci-contre.

La source chaude est constituée par le foyer, la source froide par la circulation d’eau de refroidissement du condenseur.

Les phases successives du cycle de fonctionnement de la machine sont les suivantes :

1. Admission : \(R1\) est ouvert et \(R2\) est fermé. L’eau de la chaudière se vaporise à \(p\) et \(T\) constantes, repoussant le piston vers la droite (phase motrice)

2. Détente : \(R1\) et \(R2\) sont fermés. Le piston continue à se déplacer vers la droite (phase motrice). La vapeur subit une détente adiabatique qui l’amène des conditions de température et de pression de la chaudière à celle du condenseur.

3. Échappement, condensation : \(R1\) est fermé et \(R2\) est ouvert. Le piston revient complètement vers la gauche. Le mélange liquide-vapeur obtenu en fin de détente vient se condenser entièrement dans le condenseur, à pression et température constantes (phase résistante).

4. Alimentation de la chaudière : La pompe d’alimentation comprime adiabatiquement à la pression \(P\)1 de la chaudière l’eau du condenseur et l’envoie dans la chaudière où elle s’échauffe à pression constante jusqu’à la température \(T1\) (phase résistante).

3.2. Analyse du fonctionnement

Suivons alors les transformations subies par une masse d’eau égale à l’unité lors des diverses phases du fonctionnement et reportons-les d’abord sur la diagramme de Clapeyron.

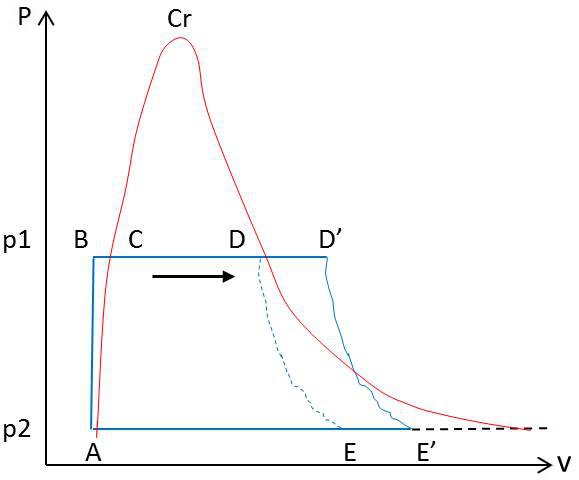Nous partirons du point \(A\) qui représente l’eau en fin de condensation juste avant qu’elle pénètre dans la pompe d’alimentation de la chaudière.

1. L’eau subit dans la pompe une compression adiabatique qui modifie très peu sa température et amène le point figuratif en \(B\), à la pression \(p_1\).

2. Puis l’échauffement isobare dans la chaudière amène le point figuratif en \(C\) sur la courbe de saturation.

3. Lors de l’admission, l’eau passe sous forme de vapeur dans le cylindre ; le point figuratif vient en \(D\).

4. La détente adiabatique amène le point figuratif en \(E\) (mélange liquide-vapeur à la pression \(p_2\) et à la température \(T_2\)  ; enfin la condensation le ramène en \(A\).

Le cycle ainsi décrit porte le nom de cycle de Rankine. Il ne représente que de loin le cycle réellement décrit par l’eau dans une machine à vapeur. La détente notamment n’est jamais poussée jusqu’à la pression du condenseur.

On l’arrête à une pression nettement inférieure et on laisse alors la vapeur s’échapper de façon irréversible dans le condenseur. Nous nous en tiendrons cependant à ce cycle particulièrement simple.

Une fois le cycle tracé dans le diagramme de Clapeyron, il suffit de mesurer son aire pour obtenir le travail fourni lors de ce cycle de transformation. La chaleur prise à la source chaude dans les portions \(BC\) et \(CD\) est aisément calculée connaissant la chaleur spécifique \(c_p\) de l’eau liquide et sa chaleur latente de vaporisation à la température \(T_1\). On en déduit le rendement de la machine.

3.3. Calculs associés

Il est évident que le problème peut être entièrement traité par le calcul. On obtiendra par exemple le travail produit au cours de la détente adiabatique en appliquant soit la formule générale \(W=-\Delta U\), soit la formule empirique de Rankine.

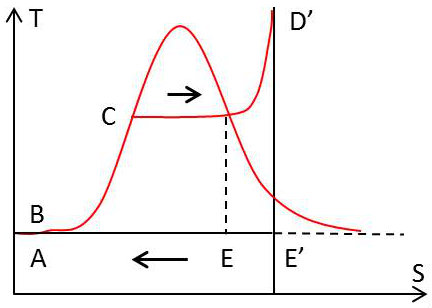Représentons maintenant le cycle de Rankine dans le diagramme entropique et dans le diagramme de Mollier.

Dans le diagramme entropique, on voit immédiatement que les points \(A\) et \(B\) sont pratiquement confondus : \[\Delta S=0\quad;\quad\Delta T\approx 0\]

En outre, la détente est représentée par la verticale \(DE\).

Le diagramme de Mollier est plus pratique pour le calcul du rendement de la machine.

La compression adiabatique (verticale \(AD\)) est suivie d’un échauffement isobare (courbe dont la pente part pratiquement de la valeur \(T_2\) pour atteindre en \(B\) la valeur \(T_1\)). Le palier \(CD\) se raccorde à cet isobare (pente constante égale à \(T_1\) ). La verticale \(DE\) et la portion de palier \(EA\) ferment le cycle.

Remarquons alors que les transformations \(BCD\) et \(EA\) étant isobares, nous pourrons écrire :

– Chaleur cédée pour la source chaude : \[Q_{BCD}=H_D-H_B\]

– Chaleur cédée pour la source froide : \[Q_{EA}=H_A-H_E\qquad\text{(négative)}\]

En supposant le fonctionnement réversible, un rendement : \[R=\frac{H_D-H_B+H_A-H_E}{H_D-H_B}=1-\frac{H_E-H_A}{H_D-H_B}\]

soit, en désignant par \(\alpha\) et \(\alpha'\) les pentes de \(AE\) et \(BD\) : \[R=1-\frac{\tan(\alpha)}{\tan(\alpha')}\]

La pente de \(BD\) étant inférieure à celle du palier de vaporisation \(CD\), c’est-à-dire \(T_1\), on voit que le rendement est inférieur à : \[R'=1-\frac{T_2}{T_1}\]

c’est-à-dire au rendement d’une machine de Carnot fonctionnant entre les deux sources \(T_1\) et \(T_2\), ceci bien que nous ayons supposé le fonctionnement réversible.

Cela vient du fait que nous devons supposer que la partie \(BC\) soit réversible, que la chaleur reçue par l’eau est successivement fournie par une infinité de sources de températures s’échelonnant entre \(T_1\) et \(T_2\). D’où un rendement plus faible que si toute la chaleur avait été fournie par la source unique .

3.4. Cycle de Hirn

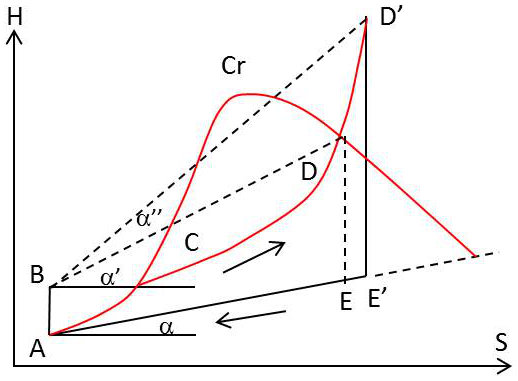
La vapeur à la sortie de la chaudière est surchauffée à pression constante avant son admission dans le cylindre. Le cycle de Hirn \(ABCD'E'A\) (voir figure précédente) de transformations parcourues par l’eau est représenté dans les trois types de diagrammes.

On a supposé sur la figure que la surchauffe n’est pas très poussée et qu’apparaît encore en fin de détente, une légère condensation. Dans la pratique, on poussera la surchauffe assez loin pour que la vapeur reste sèche en fin de détente. Ceci permet d’éviter la condensation de la vapeur sur les parois du cylindre, cause d’échanges de chaleur importants et de diminution de rendement pratique.

L’examen du diagramme de Mollier montre que le rendement : \[R'=\frac{H_{D'}-H_B-(H_{E'}-H_A)}{H_{D'}-H_E}=1-\frac{\tan(\alpha)}{\tan(\alpha')}\]

est plus grand que le rendement : \[R=1-\frac{\tan(\alpha)}{\tan(\alpha')}\]

du cycle de Rankine correspond à la même température (et par suite à la même pression) au sein de la chaudière. L’isobare \(DD'\) de la vapeur tourne en effet sa concavité vers le haut et la pente du segment \(BD'\) est supérieure à la pente de \(BD\).

On trouve dans les tables relatives à la vapeur d’eau des diagrammes de Mollier, comportant les réseaux d’isobares et d’isothermes de la vapeur, de l’eau et du mélange liquide - vapeur, ainsi que les courbes à titre \(x=cte\) . Le tracé du cycle de fonctionnement est alors immédiat et le rendement s’en déduit par lecture directe des deux pentes. De même, le taux de condensation en fin de détente se lit directement sur le diagramme.

4. Machines frigorifiques

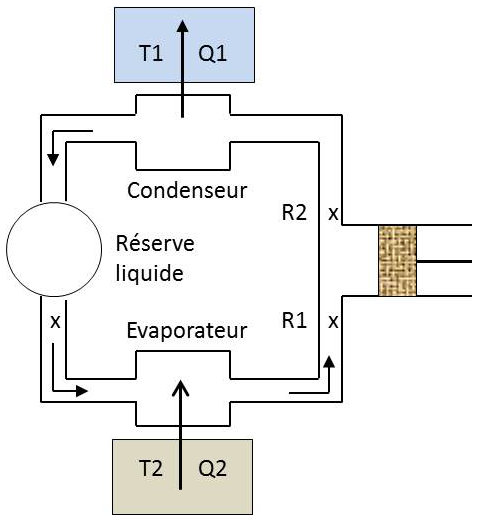Le schéma de principe d’un réfrigérateur est très voisin de celui d’une machine à vapeur. La chaudière est remplacée par un organe similaire (évaporateur) qui prend maintenant de la chaleur à la source froide et constitue l’élément réfrigérant.

Le condenseur cède de la chaleur à la source chaude (circulation d’eau ou ailettes de refroidissement par air). La seule différence provient du fait que la pression est maintenant plus forte dans le condenseur que dans l’évaporateur.

Si l’on voulait conserver une complète analogie avec la machine à vapeur, il faudrait remplacer la compression adiabatique dans la pompe d’alimentation par une détente adiabatique fournissant du travail au milieu extérieur.

La pompe d’admission serait alors remplacée par une turbine actionnée par la détente adiabatique du fluide et le cycle de fonctionnement serait un cycle de Hirn décrit en sens inverse. Ceci introduirait cependant un organe compliqué et on préfère remplacer cette détente adiabatique par une détente laminée type Joule-Kelvin où la chute de pression provient du passage du liquide dans un orifice étranglé.

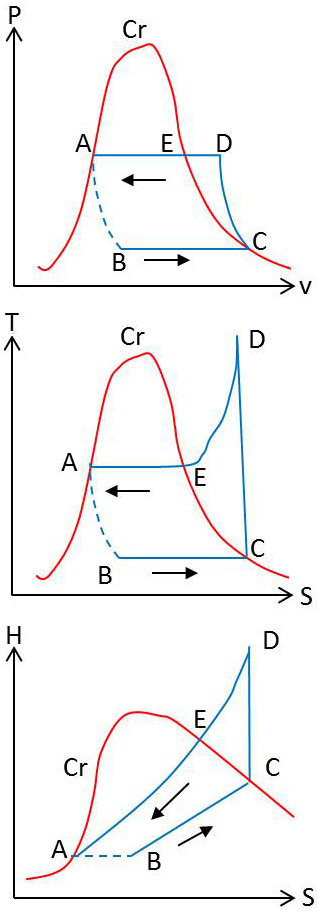Nous supposerons pour simplifier que c’est là la seule partie irréversible du cycle et nous la représentons en pointillé sur les trois diagrammes ci-contre.

Remarquons que, dans le diagramme de Mollier, la détente laminée \(AB\) est représentée par une horizontale (l’enthalpie se conserve). Le diagramme de Mollier permet là encore une représentation très simple du rendement. Celui-ci est défini par le quotient : \[\frac{\text{Chaleur extraite de la source froide }}{\text{Travail dépensé}}\]

C’est-à-dire par la formule :

\[\begin{aligned} &R=\frac{[Q_{BC}]}{-[Q_{DEA}+Q_{BC}]}\\ \text{Soit encore~:}\\ &R=\frac{[H_C-H_B]}{-[H_A-H_D+H_C-H_B]}=\frac{[H_C-H_B]}{[H_D-H_C]}\end{aligned}\]

puisque \(H_A=H_B\).

Soit en définitive un rendement d’autant meilleur que \(CD\) est plus court sur le diagramme de Mollier, c’est-à-dire d’autant meilleur que la différence de température à établir entre la source froide et la source chaude est plus faible (même conclusion que pour un cycle de Carnot).

On trouve par exemple pour un réfrigérateur utilisant comme fluide l’ammoniac :

• Température de l’évaporateur : –15 °C

• Température du condenseur :   +30 °C

• Rendement théorique :R = 4,76

alors que le rendement d’un réfrigérateur de Carnot fonctionnant entre les mêmes températures serait 258/45 = 5,73. En fait, le rendement est nettement plus faible que 4,76, les causes d’irréversibilité étant loin de se réduire à la seule partie \(AB\) du cycle.