1. Fugacité d’un gaz réel
Considérons une mole d’un gaz réel. Nous fixons sa température à une valeur donnée \(T\) et abaissons sa pression jusqu’à une valeur très faible \(\varepsilon\). Le gaz a alors les propriétés d’un gaz parfait, notamment sa fonction de Gibbs est donnée par : \[G^m=R~T~\{\Phi+\ln(\varepsilon)\}\]
\(\Phi\) étant comme nous l’avons vu fonction seulement de la température, nous maintenons cette dernière constante de sorte que \(\Phi\) reste invariable.
Cette expression de \(G^m\) n’est valable que tant que la pression est extrêmement faible. Si la pression passe à une valeur plus importante \(p\), nous pourrons déduire de l’équation d’état, en remarquant que, \(T\) restant constante : \[G^m(p)=G^m(\varepsilon)+\int_{\varepsilon}^p v~dp\]
Nous définirons alors la fugacité \(f\) du gaz, à la température \(T\) et à une pression quelconque, par la relation : \[G^m=R~T~\{\Phi+\ln(f)\}\]
La relation précédente permet de calculer \(f\) à toute pression si l’on connaît l’équation d’état. Aux basses pressions : \[\ln(f)-\ln(p)\rightarrow 0\qquad\text{et, par suite :}\quad\frac{f}{p}\rightarrow 1\quad\text{quand}~p\rightarrow 0\]
L’introduction de la fugacité étend donc la notion de pression et permet d’écrire à toute pression la fonction de Gibbs sous la forme : \[G^m=R~T~\{\Phi+\ln(f)\}\]
identique à celle que l’on obtient dans le cas du gaz parfait. La simplification n’est évidemment qu’une simplification d’écriture et n’a aucun intérêt si l’on veut passer aux applications.
2. Fugacité partielle des constituants d’un système chimique
Soit un système chimique de plusieurs phases en équilibre (nous supposons toujours qu’il ne se produit pas de réaction chimique). L’une de ces phases est une phase gazeuse. Le potentiel chimique du constituant \(i\) est le même dans toutes les phases. Choisissons la phase gazeuse.
Si sa pression est aussi faible pour qu’on puisse l’assimiler à un mélange de gaz parfaits, le potentiel chimique \(\mu_i\) y est égal à : \[\mu_i=R~T~\{\Phi_i+\ln(p_i)\}\]
\(p_i\) étant la pression partielle du constituant \(i\) dans cette phase gazeuse.
S’il n’est pas possible d’assimiler à un gaz parfait la phase gazeuse, nous écrirons le potentiel chimique sous la forme : \[\mu_i=R~T~\{\Phi_i+\ln(f_i)\}\]
introduisant ainsi des quantités \(f_i\) que nous nommons fugacités partielles des divers constituants du système. À l’équilibre, la fugacité d’un constituant donné est la même dans toutes les phases, d’où le nom de fugacité ou tendance à s’échapper. Le constituant tendant également à s’échapper de chacune des phases, sa concentration dans chacune d’elles reste constante au cours du temps.
L’introduction des \(f_i\) n’apporte rien de nouveau en ce qui concerne les calculs, mais elle a ceci de commode qu’on pourra remplacer simplement les \(f_i\) par des pressions partielles dans la phase gazeuse chaque fois que cette dernière pourra être assimilée à un gaz parfait.
Les formules que nous allons établir seront donc rigoureuses tant qu’elles contiendront les fugacités partielles. Nous devrons les considérer comme approximatives dès que nous y aurons remplacé ces fugacités par les pressions partielles dans la phase gazeuse.
L’important sera de se souvenir que la fugacité d’un constituant donné est la même (à l’équilibre) dans toutes les phases solides, liquides ou gazeuses.
3. Applications aux solutions
Nous nous bornerons aux solutions liquides, formées d’un solvant et d’un seul corps dissous ou soluté. Nous désignerons sous le nom de solvant le corps dont la concentration moléculaire est la plus forte ; en fait, une telle distinction n’est pas nécessaire et la solution est simplement un système formé à partir de deux constituants.
Nous supposerons pour le moment que le système comporte deux phases, une liquide et une gazeuse. Nous supposerons en outre que l’équilibre peut avoir lieu sans que la pression de la phase liquide soit forcément égale à la somme des pressions partielles des deux constituants dans la phase gazeuse. Expérimentalement, on peut y arriver de deux manières :
-
Soit en ajoutant à la phase gazeuse une certaine quantité d’un gaz inerte (gaz ne réagissant pas sur les constituants gazeux et insoluble dans la phase liquide). On peut ainsi varier à volonté la pression totale de la phase liquide indépendamment des pressions partielles des constituants dans la phase gazeuse.
-
Soit en séparant la phase liquide de la phase gazeuse par une cloison poreuse, imperméable à la phase liquide (tension capillaire) et laissant passer librement la phase gazeuse qui vient à travers les pores se mettre à l’équilibre avec une phase liquide dont la pression totale \(p\) peut être variée arbitrairement.
Portons alors notre attention sur la phase liquide et écrivons l’équation de Gibbs-Duhem liant les variations \(d\mu_1,~d\mu_2,~dT,~dp\) dans une transformation réversible quelconque : \[n_1~d\mu_1+n_2~d\mu_2+S~dT-v~dp=0\]
Introduisons les fugacités dans les deux constituants. On a :
\[\begin{aligned} d\mu_1&=R~T~\frac{df_1}{f_1}\\ d\mu_2&=R~T~\frac{df_2}{f_2}\end{aligned}\]
Désignant par \(n\) le nombre de moles total de la phase liquide, par \(x_1,~x_2\) les concentrations moléculaires des constituants dans cette phase, il vient pour toute variation \(dp\) de la pression totale à température constante : \[x_1~\frac{df_1}{f_1}+x_2~\frac{df_2}{f_2}=\frac{v~dp}{n~R~T}=\frac{p~v}{n~R~T}~\frac{dp}{p}\]
Or, \(p~v\ll n~R~T\) (phase liquide) et, par suite, les variations relatives de fugacité des deux constituants lors d’une variation de la pression totale de la phase liquide sont négligeables, tant que cette variation de pression n’est pas très grande. Il en est de même des variations relatives des pressions partielles, dans la phase gazeuse, des constituants 1 et 2.
Supposons alors que la phase liquide soit soumise à sa seule pression de vapeur, et supposons que cette dernière est relativement faible. Les fugacités des constituants dépendent en toute rigueur, non seulement de leurs concentrations moléculaires, mais de la pression de vapeur (on suppose \(T=cte\)).
Nous ne pourrons pas négliger l’influence de la pression sur les fugacités et considérer qu’elles ne dépendent que des concentrations. Nous écrirons alors l’équation de Gibbs-Duhem sous la forme qu’elle prendrait à \(p\) et \(T\) constantes, cela n’entraînerait qu’une erreur négligeable :
\[\begin{aligned} n_1~d\mu_1+n_2~d\mu_2&=0\\ \text{ou encore :}\quad x_1~\frac{df_1}{f_1}+x_2~\frac{df_2}{f_2}&=0\end{aligned}\]
Assimilons alors les \(f_i\) aux pressions partielles dans la phase vapeur. Nous obtenons, en remarquant que toute variation de concentration entraîne des variations \(dx_1,~dx_2\) telles que :
\[\begin{aligned} dx_1&=-dx_2\\ \frac{dp_1}{dx_1}/\frac{dp_2}{dx_2}&=\frac{p_1}{x_1}/\frac{p_2}{x_2}\end{aligned}\]
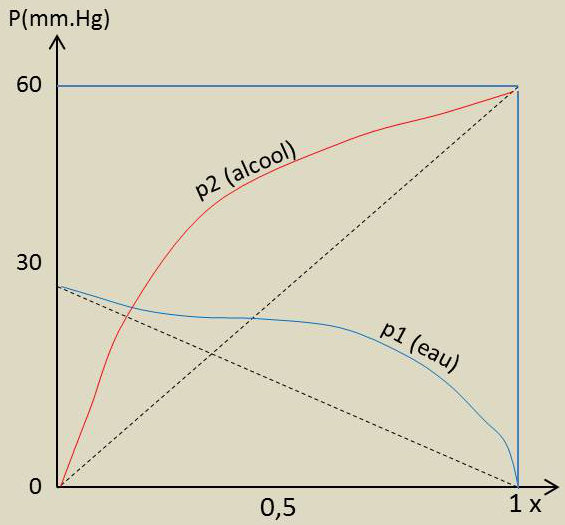 Portons sur un diagramme, en fonction de la concentration dans la phase liquide du constituant 2, soit \(x_2\), les pressions partielles dans la phase vapeur des constituants 1 et 2.
Portons sur un diagramme, en fonction de la concentration dans la phase liquide du constituant 2, soit \(x_2\), les pressions partielles dans la phase vapeur des constituants 1 et 2.
La figure ci-contre correspond au cas du mélange eau - alcool. La connaissance d’une courbe permet de construire entièrement l’autre. Elle représente les pressions de vapeur (partielles) du mélange eau - alcool éthylique à 25 °C.
3.1. Mélanges idéaux
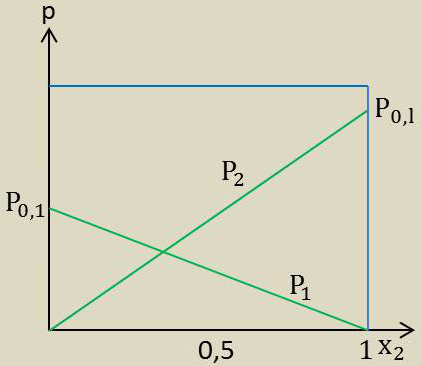 Il peut arriver que l’une des deux courbes soit une droite (voir figure ci-contre) ; l’autre est alors une droite également. Les mélanges ayant cette propriété sont des mélanges idéaux.
Il peut arriver que l’une des deux courbes soit une droite (voir figure ci-contre) ; l’autre est alors une droite également. Les mélanges ayant cette propriété sont des mélanges idéaux.
Il est nécessaire pour que le mélange soit idéal que les deux constituants aient des propriétés très voisines. Citons le cas du mélange de chlorobenzène et de bromobenzéne, etc.
On a alors, en désignant par \(p_1^0,~p_2^0\) les pressions de vapeur des constituants purs à la température considérée : \[p_1=p_1^0~x_1\quad;\quad p_2=p_2^0~x_2\]
3.2. Solutions étendues
Même si le mélange n’est pas idéal, les solutions étendues présentent des propriétés qui les apparentent aux mélanges idéaux. Nous désignons par \(x_2\) la concentration moléculaire (faible) du soluté supposé évidemment non dissocié.
On a toujours en toute rigueur, en introduisant à nouveau les fugacités : \[\frac{df_1}{dx_1}/\frac{df_2}{dx_2}=\frac{f_1}{x_1}/\frac{f_2}{x_2}\]
et l’expérience montre (on peut le démontrer par la mécanique statistique) que \(df_2/dx_2\) tend vers une limite finie et non nulle quand \(x_2\) tend vers 0.
On a alors, pour \(x_2\approx 0\) : \(\cfrac{df_2}{dx_2}\approx\cfrac{f_2}{x_2}\)
et par suite, pour \(x_2\approx 1\) : \(\cfrac{df_1}{dx_1}\approx\cfrac{f_1}{x_1}\)
Assimilons les \(f_i\) aux pressions partielles dans la phase gazeuse.
Quand la concentration \(x_2\) du soluté est faible, \(dp_2/dx_2\approx p_2/x_2\), ce qui exprime simplement que la courbe des pressions partielles du soluté est au départ voisine de sa tangente à l’origine, soit : \(p_2\approx k_2~x_2\quad(k_2=cte)\).
La relation \(dp_1/dx_1\approx p_1/x_1\) pour \(x_1\approx 1\) nous apprend alors que la courbe \(p_1\), à sa rencontre avec l’axe des \(p\), admet pour tangente la droite tracée en pointillé, ce qui est beaucoup moins évident.
3.3. Loi de Henry
Supposons alors que le solvant ne soit pas volatil, et que le soluté soit un gaz qui figure pratiquement seul dans la phase gazeuse. Le fait que \(p_2\approx k_2x_2~;~x_2\approx 0\) exprime la loi de Henry suivant laquelle :
La concentration moléculaire de la solution d’un gaz est proportionnelle à la pression du gaz au-dessus de la solution tant que cette pression n’est pas trop forte.
Nous avons vu qu’on pouvait en déduire la loi de Van’t Hoff sur la pression osmotique de la solution de ce gaz considéré comme parfait.
3.4. Loi de Raoult
Supposons maintenant le solvant volatil et le soluté non volatile. Soit \(p_1^0\) la pression de vapeur du solvant pur et \(p\) la pression de vapeur de la solution diluée où la concentration moléculaire du solvant est \(x_1\) et sa pression \(p_1\) et celle du soluté est \(x_2\) et sa pression \(p_2\).
\(x_2\) étant petit, on peut écrire : \[\frac{dp_1}{dx_1}=\frac{p_1}{x_1}\qquad\text{soit :}\quad\frac{dp_1}{p_1}=\frac{-dx_2}{1-x_2}\]
En intégrant : \[\ln~\frac{p_1}{p_1^0}=\ln(1-x_2)\Rightarrow p_1=p_1^0~(1-x_2)\]
On en conclut que l’abaissement relatif de tension de vapeur de la solution qui résulte de la présence d’une concentration moléculaire \(x_2\) de soluté est : \[\frac{\Delta p}{p}=\frac{p_1^0-p_1}{p_1^0}=x_2\]
Il est par suite égal à la concentration moléculaire du soluté. C’est la loi de Raoult.
3.5. Loi de Van’t Hoff sur la pression osmotique
Nous avions déjà déduit cette loi de la loi de Henry dans le cas de la solution d’un gaz parfait dans un solvant non volatil. Montrons qu’elle est valable pour toute solution étendue d’un soluté quelconque ; ceci nous permettra de mieux comprendre la raison d’être de la pression osmotique.
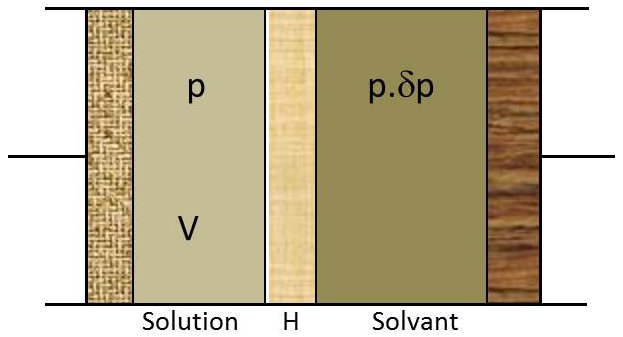 Dans un corps de pompe fermé par deux pistons et partagé en son milieu par une cloison hémiperméable (perméable au seul solvant), plaçons \(n\) moles du solvant pur liquide (compartiment de droite) et une solution contenant \(n_1\) moles de solvant et \(n_2\) moles de soluté (compartiment de gauche, \(n_2\ll n_1\)).
Dans un corps de pompe fermé par deux pistons et partagé en son milieu par une cloison hémiperméable (perméable au seul solvant), plaçons \(n\) moles du solvant pur liquide (compartiment de droite) et une solution contenant \(n_1\) moles de solvant et \(n_2\) moles de soluté (compartiment de gauche, \(n_2\ll n_1\)).
Maintenons le tout à la température \(T\) et cherchons d’abord, grâce aux pistons, à établir la même pression totale dans les deux compartiments. Nous observons alors que l’équilibre n’est pas possible dans ces conditions.
En effet, la cloison centrale est perméable au solvant (constituant 1). L’équilibre exige donc que son potentiel chimique soit le même dans le solvant pur et la solution. Ceci n’est évidemment pas possible, tout au moins si le solvant et la solution sont à la même pression totale. Dans ce cas, le potentiel chimique du solvant dans la solution est inférieur à celui du solvant dans le solvant pur.
Le solvant pur du compartiment de droite va donc, en raison de sa fugacité supérieure, pénétrer constamment dans le compartiment de gauche. Si la pression est constamment maintenue égale des deux côtés, tout le solvant va peser dans la solution. C’est ce qui se passe lorsqu’une cellule végétale, contenant une solution de sels minéraux, est plongée dans l’eau pure ; l’eau pénètre constamment dans la cellule et l’on voit cette dernière se gonfler.
Nous allons cependant pouvoir réaliser l’équilibre en nous autorisant du fait que le potentiel chimique des deux constituants de la solution dépend un peu de la pression totale. Il doit donc exister une possibilité de réaliser l’équilibre en établissant grâce aux pistons une différence de pression entre les deux compartiments.
Pour le calculer, désignons par \(\mu_1^0,~f_1^0\) le potentiel chimique et la fugacité du solvant pur. Dans la solution de concentration moléculaire en soluté, la fugacité du solvant est : \[f_1=f_1^0~(1-x_2)\qquad\text{(la solution étant très diluée)}\]
Nous en tirons (\(x_2\) petit) : \[R~T~\ln(f_1)-R~T~\ln(f_1^0)=R~T~\ln(1-x_2)\approxeq -R~T~x_2\]
L’introduction de \(n_2\) moles de soluté, à pression et température constantes, fait donc varier le potentiel chimique du solvant de : \[\mu_1-\mu_1^0=\delta\mu_1=-R~T~x_2=-R~T~\frac{n_2}{n_1+n_2}\approxeq R~T~\frac{n_2}{n_1}\]
Pour que le solvant pur soit en équilibre avec la solution, il nous faut modifier sa pression de façon à introduire la même variation dans son potentiel chimique. Or, dans le solvant pur \(\mu_2=0\) et pour une variation de pression à \(T\) cte : \[n_1~d\mu_1-v~dp=0\quad\Rightarrow\quad d\mu_1=\frac{v}{n_1}~dp\]
Le solvant pur étant très peu compressible, \(v\) est à peu près indépendant de \(p\). En outre, remarquons que \(v\) volume de \(n_1\) moles de solvant pur est aussi très sensiblement le volume de la solution puisque sa concentration en soluté est très faible.
Pour obtenir la variation \(\delta\mu_1\) du potentiel chimique du solvant pur, il nous faut donc faire varier sa pression de : \[\delta p=\frac{n_1}{v}~\delta\mu_1=-\frac{n_2~R~T}{v}\]
Ce qui revient à dire que, pour que l’équilibre ait lieu, il faut que la pression de la solution excède celle du solvant pur d’une quantité \(\varpi=-\delta p\), ce qui est tout simplement la pression osmotique et dont la valeur est : \[\varpi=\frac{n_2~R~T}{v}\]
-
\(v\) : volume de la solution diluée,
-
\(n_2\) : nombre de moles de soluté dissous dans ce volume
C’est la loi de Van’t Hoff.
3.6. Cryométrie
Nous allons maintenant calculer la différence des températures de congélation, à la pression atmosphérique, entre le solvant pur et la solution que nous supposerons toujours très diluée en soluté.
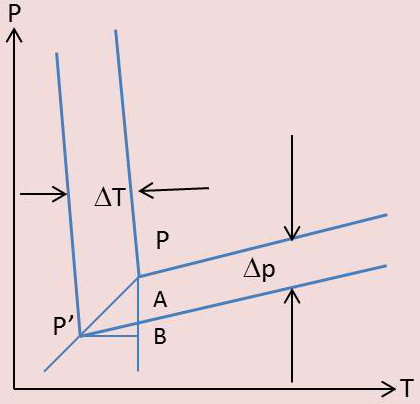 Nous traçons dans ce but dans le diagramme \(p,~T\) les courbes d’équilibre solide - liquide, liquide - vapeur et solide - vapeur relatives au solvant pur, ou plus exactement la partie de ces courbes avoisinant immédiatement le point triple \(P\).
Nous traçons dans ce but dans le diagramme \(p,~T\) les courbes d’équilibre solide - liquide, liquide - vapeur et solide - vapeur relatives au solvant pur, ou plus exactement la partie de ces courbes avoisinant immédiatement le point triple \(P\).
Cherchons maintenant à tracer les mêmes courbes pour la solution.
La courbe de vaporisation (liquide - vapeur) de la solution est obtenue par simple translation verticale (vers le bas) de la courbe de vaporisation du solvant pur. Ceci résulte de la loi de Raoult : \[\Delta p=-p_1^0~x\]
\(p\) varie peu dans l’intervalle de température couvert par le diagramme qui, rappelons-le, est très étalé et n’indique en réalité que les variations de \(p\) et \(T\) autour du point triple.
Nous supposons le soluté non volatil. La phase gazeuse ne contient donc que la vapeur du solvant pur. Quand nous refroidissons suffisamment la solution (diluée), la phase solide qui apparaît est formée de cristaux de solvant pur, c’est-à-dire sur la courbe de sublimation du solvant pur, courbe qui se trouve ainsi commune au solvant et à la solution diluée.
Soit \(P'\) ce point triple. Par \(P'\) passe la courbe de congélation commençante de la solution, décalée de vers la gauche par rapport à celle du solvant pur (voir figure). Menons de \(P\) la verticale \(PAB\), de \(P\) l’horizontale \(P'B\). On a évidemment :
\[\begin{aligned} &\Big(\frac{dp}{dT}\Big)_{vap}=\frac{BA}{P'B}\\ &\Big(\frac{dp}{dT}\Big)_{subl}=\frac{BP}{P'B}\end{aligned}\]
Remarquons que les courbes de fusion sont presque verticales, \((dp/dt)_{fus}\) étant presque très grand, et, par suite, \(P'B\approx\Delta T\). De plus, \(AP=\Delta P\). Nous avons alors : \[\frac{\Delta p}{\Delta T}=\frac{BP-AB}{P'B}=\Big(\frac{dp}{dT}\Big)_{sub}-\Big(\frac{dp}{dT}\Big)_{vap}\]
La formule de Clapeyron donne :
\[\begin{aligned} \Big(\frac{dp}{dT}\Big)_{vap}=\frac{1}{T_0}~\frac{L_v}{u''-u'}\approxeq\frac{1}{T_0}~\frac{L_v}{u''}\\ \Big(\frac{dp}{dT}\Big)_{sub}=\frac{1}{T_0}~\frac{L_s}{u''-u'}\approxeq\frac{1}{T_0}~\frac{L_s}{u''}\end{aligned}\]
-
\(T_0\) : température du point triple ;
-
\(u',u\) : volumes spécifiques du liquide et du solide, négligeables devant \(u''\) volume spécifique de la vapeur.
Nous en tirons :
\[\begin{aligned} \frac{\Delta p}{\Delta T}&=\frac{1}{T}~\frac{L_s-L_v}{u''}=\frac{1}{T_0}~\frac{L_f}{u''}\\ \text{soit :}\quad T&=T_0~\frac{u''~p}{L_f}\end{aligned}\]
Mais : \[\Delta p=p_1^0~x \qquad \text{et}\qquad p_1^0~u''=\frac{R~T}{M_0}\]
la vapeur étant sensiblement un gaz parfait, \(M_0\) étant la masse molaire du solvant.
On obtient en définitive pour l’abaissement \(\Delta T\) du point de congélation : \[\Delta T=\frac{R~T_0^2}{M_0~L_f}~x\]
On préfère généralement représenter la concentration de la solution par sa molarité (nombre de moles dissoutes dans 1 kg de la solution). Si \(M_0\) étant la masse du solvant, 1 kg de solution contient pratiquement, la concentration étant faible : \(1000/M_0\) moles de solvant. La concentration moléculaire du soluté est donc : \[x=\frac{M_0}{1000}~m\]
De plus, nous avons exprimé évidemment \(L_f\) en joules. Si \(L_f\) était exprimée en calories, on écrirait alors : \[\Delta T=\frac{R~T_0^2}{J~L_f} \qquad J=4,18~:~\text{équivalent mécanique de la calorie}\]
Dans le cas de l’eau : \[L_f=80~cal~;~T_0=273~K~;~M_0=18\quad\Rightarrow\quad \Delta T=1,86~m\]
C’est bien ce que vérifie l’expérience.
4. Étude complète de la solidification d’un mélange binaire
Pour étudier la solidification d’un mélange binaire, nous nous bornerons à l’exemple du mélange or - thallium dont la solidification va nous conduire au phénomène de la formation d’un eutectique.
Le système que nous considérons est donc un mélange d’or et de thallium dont nous supposons la masse totale égale à l’unité de masse, soit 1 kg. Ce mélange est tout d’abord défini par sa concentration globale en l’un des constituants. Nous représenterons cette concentration par le nombre \(c\) qui représente la proportion de thallium dans la masse totale. Cette masse totale étant ici 1 kg, le nombre \(c\) représente la masse de thallium (en kg) que contient le système, \((1-c)\) représentant la masse d’or.
Nous partons d’un état initial où la température est assez élevée pour qu’aucune phase solide ne figure dans le mélange ; ce dernier est supposé contenu dans un corps de pompe où un piston permet de régler la pression à une valeur fixée une fois pour toutes (1 atm par exemple). Nous ne considèrerons jamais de températures assez élevées pour que la pression de vapeur du mélange puisse atteindre 1 atm.
Le piston est donc au contact direct des phases condensées et aucune phase vapeur n’apparaît. La variance du système est donc \(c+2-\Phi\), mais nous imposons la pression. Le nombre de paramètres tels que concentrations ou température dont nous pouvons varier arbitrairement la valeur à l’équilibre est donc \(V'=c+1-\Phi\). \(V'\) est donc la variance du système à pression totale imposée.
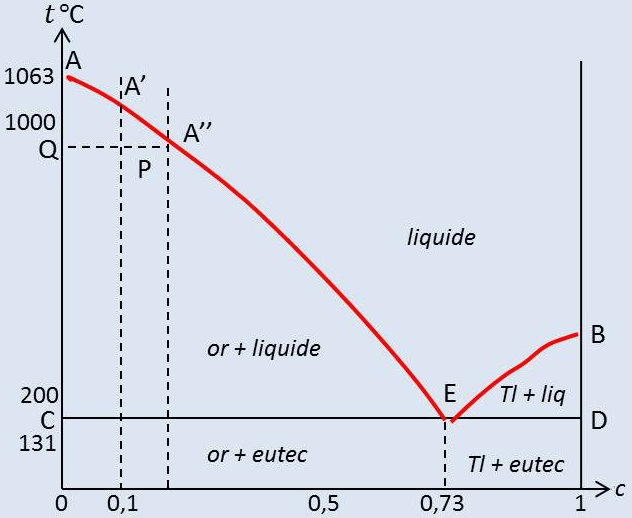 Sur le diagramme ci-contre, nous représentons l’état du système par sa composition globale \(c\) que nous portons en abscisses et sa température \(t\) (en °C) que nous portons en ordonnée.
Sur le diagramme ci-contre, nous représentons l’état du système par sa composition globale \(c\) que nous portons en abscisses et sa température \(t\) (en °C) que nous portons en ordonnée.
Supposons d’abord \(c=0\) (or pur) et \(t\) élevée. Il y a alors un constituant (l’or) et une phase (liquide), soit \(V'=1\).
Nous pouvons faire varier \(t\) arbitrairement. Abaissons \(t\) jusqu’à 1063 °C où apparaît le début de congélation. De l’or solide se dépose \((\Phi=2~;~V'=0)\).
Tant que le liquide subsiste en présence du solide, \(t\) va rester fixe à 1063 °C. Quand tout le liquide a disparu, nous pouvons abaisser \(t\) à volonté. Le point \(A\) correspond à l’équilibre or liquide - or solide. Le même résultat aurait été obtenu pour \(c=1\) (thallium pur) et le point \(B\) est le point de fusion du thallium pur.
Partons maintenant d’un mélange contenant 10 % de thallium. Son point de congélation est abaissé par la présente du soluté (thallium) et le dépôt d’une phase solide n’apparaît qu’à environ 1000 °C. Le dépôt est constitué par de l’or pur.
Le système comprend 2 phases, 2 constituants et \(V'=1\) . Nous pouvons donc abaisser \(t\) ; de plus en plus d’or se dépose et la solution s’enrichit en thallium. Arrêtons-nous par exemple au moment où assez d’or s’est déposé pour que la solution contienne 20 % de thallium. Nous sommes alors à la température où la congélation aurait commencé si la concentration de départ du mélange avait été de 20 %. En effet, la température est égale à la température d’équilibre (à 1 atm) de l’or solide et d’un mélange liquide à 20 % de thallium.
L’état de notre système est représenté par le point \(P\), sur l’horizontale \(QA"\). Le point \(P\) indique la température et la composition globale du mélange ; il indique aussi le rapport des masses de solide (or) et de liquide. En effet, la masse totale de thallium est \(c_p\) ; si \(m_1\) est la masse de liquide (de concentration \(c_{A'}\) en thallium), on peut écrire : \[c_p=m_l~c_{A'}\quad\Rightarrow\quad m_l=\frac{c_p}{c_{A'}}\quad\Rightarrow\quad\frac{m_l}{m_s}=\frac{QP}{PA''}\]
La position de \(P\) sur l’horizontale \(QA''\) indique donc le rapport des masses de solide \(m_s\) et de liquide \(m_l\) en présence.
Abaissons toujours \(t\) ; le liquide s’enrichit de plus en plus en thallium et la succession des points figuratifs de la phase liquide décrit la courbe \(AB\). Partant d’un mélange riche en thallium, nous aurions obtenu les mêmes phénomènes, mais le point figuratif de la phase liquide à l’équilibre avec le solide aurait décrit la courbe \(BE\), la phase solide étant constituée par du thallium pur.
Les courbes \(AE\) et \(BE\) se rencontrent en \(E\) dont l’abscisse correspond à une concentration de 73 % en thallium. Si la concentration de départ dans la phase liquide est précisément 73 %, on observe par refroidissement le dépôt, à la température \(t_E\), d’un mélange d’or et de thallium solides de concentration exactement égale à celle de la solution, qui se comporte donc à ce point de vue comme un corps pur ; ce mélange est désigné sous le nom de mélange eutectique.
Tant que la solution existe en présence de l’eutectique solide, le nombre de phases est 3 (liquide, or solide et thallium solide) ; le système est invariant et la température se trouve fixée à \(t_E\), la température de fusion de l’eutectique. Quand tout le liquide a disparu, le mélange eutectique redevient monovariant et la température peut s’abaisser suivant la verticale de \(E\).
Refroidissons maintenant un mélange tel que celui du point \(P\) ; la phase liquide se concentre jusqu’à ce que son point figuratif vienne en \(E\) ; alors commence à précipiter le mélange eutectique qui se dépose sur les cristaux d’or préexistants. Tant qu’il subsiste du liquide, le point figuratif reste en \(P'\) sur l’horizontale de \(E\) (le système contenant 3 phases et \(V'\) étant nul).
Les mêmes phénomènes se seraient produits si nous étions partis d’un mélange riche en thallium, le liquide s’enrichissant en or par suite du dépôt de thallium jusqu’à ce que son point figuratif vienne en \(E\). Nous pouvons donc en définitive séparer le diagramme en quatre régions :
-
au-dessous de \(AEB\), phase liquide unique, de composition et température arbitraires (dans certaines limites) : \(V'=2\) ;
-
région \(AEC\) : liquide + or solide, la composition des deux phases étant imposée lorsque \(T\) est fixée (celle de la phase solide est toujours la même) : \(V'=1\) ;
-
région \(BED\) : mêmes remarques que pour \(AEC\), mais la phase solide est formée de thallium pur : \(V'=1\) ;
-
au-dessous de \(CD\), 2 phases solides, de compositions imposées (or pur et thallium pur). La température est arbitraire, dans certaines limites : \(V'=1\).
On peut aussi, partageant la région 4 en deux parties, à gauche et à droite de la verticale de \(E\), considérer que dans la première le solide est formé d’un mélange d’or et d’eutectique, dans la seconde d’un mélange de thallium et d’eutectique.
Remarque
Dans la pratique, on n’isole pas les phases condensées par un piston éliminant la phase vapeur ; le mélange est placé dans une atmosphère inerte (argon par exemple) maintenue à une pression constante (atmosphérique par exemple). Une phase supplémentaire apparaît alors (gazeuse), mais aussi un constituant supplémentaire, et la variance ne change pas.
Les pressions partielles de l’or et du thallium dans la phase gazeuse se règlent constamment à une valeur égale à la fugacité du constituant correspondant dans les phases condensées ; aux températures que nous avons considérées, ces pressions partielles sont très faibles et la quantité d’or et de thallium située dans la phase vapeur négligeable ; nos conclusions restent alors strictement valables.
Le cas que nous avons étudié est un cas particulièrement simple (pas de solution solide des deux constituants, ni combinaison donnant naissance à un composé défini, miscibilité des liquides en toutes proportions). L’étude du cas général sortirait du cadre de ce cours.

