1. Fonctions caractéristiques du canal ionosphérique

1.1. Fonction de diffusion

Pour un sondeur émettant un signal \(e(t)\) et qui reçoit l’écho \(y(t)\), le canal ionosphérique se comporte comme un filtre linéaire mais non stationnaire et fortement bruité.

Un système non stationnaire ou paramétrique peut être décrit par sa réponse bitemporelle \(h(t,\tau)\) qui représente la réponse d’un filtre au temps \(t\) à une excitation de Dirac émise au temps \((t-\tau)\).

Il faut noter que \(t\) est le temps courant alors que \(\tau\) est le temps de propagation. La réponse du filtre est : \[y(t)=\int_R h(t,~\tau)~x(t-\tau)~d\tau\]

Le système peut être caractérisé par la transformée de Fourier de la réponse \(h(t,\tau)\) en fonction des variables \(t\) ou \(\tau\) ou des deux.

Pour fixer les idées, prenons l’exemple de la fonction \(D(\nu,\tau)\) : \[D(\nu,\tau)=\int_R h(t,~\tau)~\exp(-j~2\pi~\nu~t)~dt\]

Et revenant à l’expression de la réponse du filtre : \[y(t)=\iint_{R^2}D(\nu,~\tau)~x(t-\tau)~\exp(j~2\pi~\nu~t)~d\nu~d\tau\]

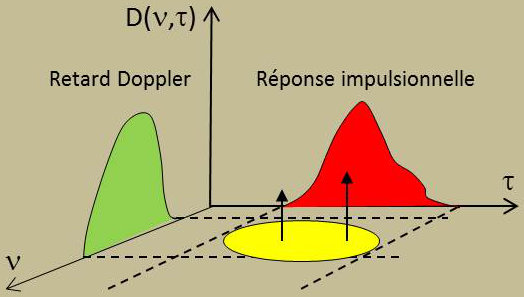La fonction \(D(\nu,~\tau)\) peut être interprétée comme une fonction de pondération dans une représentation retard Doppler. La propagation est faite de plusieurs trajets (modes) : cette fonction exprime l’atténuation de l’écho retardé de \(\tau\) dans le temps et translatée de \(\nu\) en fréquence.

Cette fonction fournit plus d’informations que la seule réponse impulsionnelle ou le seul spectre Doppler. Elle donne la distribution des modes (spatial et temporel). L’effet de dispersion du canal ionosphérique est entièrement caractérisée.

Le signal \(y(t)\) peut être considéré comme la somme pondérée d’échos réfléchis par une cible mobile dans le milieu (ions dans un plasma, véhicule en communications avec les mobiles).

Introduisant l’aspect probabiliste, on peut montrer que l’on peut écrire : \[E\{\widetilde{D}(\nu,~\tau)~\widetilde{D}(\nu',~\tau')\}=D(\nu,~\tau)~D(\nu-\nu',~\tau-\tau')\]

La fonction \(D(\nu,~\tau)\) est appelée fonction de diffusion.

1.2. Fonction d’ambiguïté

La réponse impulsionnelle d’un filtre linéaire et invariant dans le temps est exprimée à partir de l’intercorrélation entre la sortie et l’entrée. Dans le cas d’un système non stationnaire, ce sera la fonction d’interambiguïté.

Les signaux sont supposés à bande étroite et exprimés sous la forme analytique classique.

\(x_e\) étant le signal modulant et \(f_0\) la porteuse, posons : \[x_s(t)=x_e(t)~\exp(j~2\pi~f_0~t)\]

La fonction d’ambiguïté est définie par : \[\chi_{x~y}(f,~t)=\int_R x(t)~\overline{y}(t-\tau)~\exp(-j~2\pi~f~t)~dt\]

Si \(y_e\) désigne le signal reçu : \[\chi_{y_e~x_s}(f_d,~t_p)=\iint_{R^2}\chi_{x_s~x_s}(f_d-f,~t_p-\tau)~D(f,~\tau)~\exp\{-j~2\pi~(f_0-f)~t\}~df~d\tau\]

\(chi_{ss}\) est la fonction d’autoambiguïté.

1.3. Mesure de la fonction de diffusion

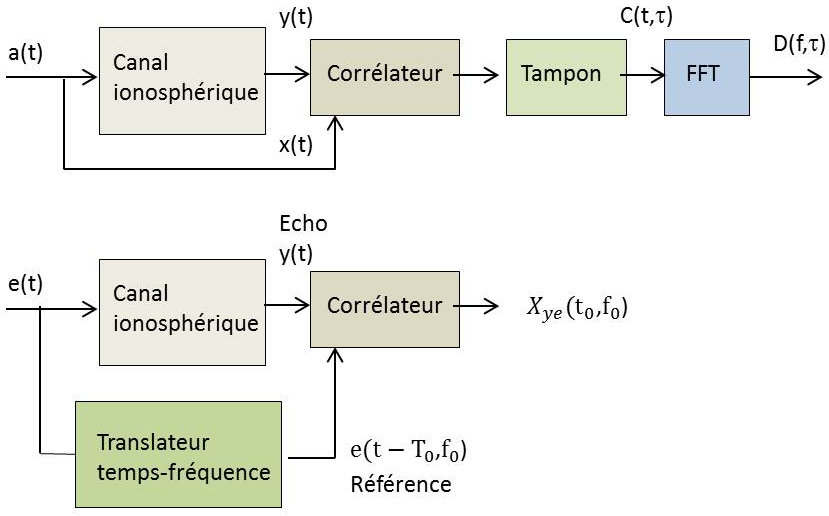
Il existe deux méthodes de mesure de la fonction de diffusion : la méthode par FFT (transformation rapide de Fourier) et la mesure par la fonction d’ambiguïté. La seconde est plus générale.

\[\begin{aligned} \qquad\\ \qquad\\ \qquad\\ \qquad\\ \qquad\\ \qquad\\ \qquad\\ \qquad\\ \qquad\\ \qquad\\ \qquad\end{aligned}\]

2. Mesure des paramètres ionosphériques

La mesure des paramètres ionosphériques s’effectue presque exclusivement par des procédés radioélectriques, à partir de stations placées au sol. Trois types de sondages sont plus particulièrement employés :

• les sondages zénithaux ;

• les sondages bistatiques :

• les sondages par rétrodiffusion.

2.1. Sondages zénithaux

La méthode par sondages zénithaux consiste à appliquer la technique du radar à l’ionosphère faisant office de cible et permet la mesure directe du temps de propagation de groupe.

L’enregistrement du temps de propagation en fonction de la fréquence d’émission f (ou de son logarithme), est appelé ionogramme zénithal. Cet ionogramme présente un grand intérêt, car il permet la lecture directe des fréquences critiques des couches.

Malheureusement, il ne donne pas l’altitude réelle de réflexion des ondes, donc il ne permet pas de déduire directement le profil vertical d’ionisation. Celui-ci peut être néanmoins calculé par des procédés complexes nécessitant l’emploi d’ordinateurs puissants.

Le sondeur zénithal est actuellement le système de prospection le plus répandu, car il constitue un moyen simple et précis et son automatisation est aisée. Il possède cependant l’inconvénient de ne permettre l’étude que du domaine ionosphérique situé à la verticale de la station.

2.2. Sondages bistatiques

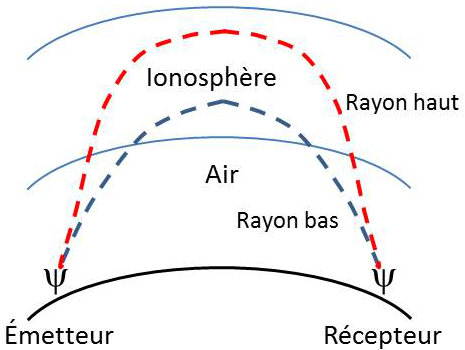La méthode par sondages bistatiques consiste à mesurer le temps de propagation de groupe d’une impulsion HF entre deux stations pouvant être éloignées de plusieurs milliers de kilomètres

Ainsi, les spécialistes noteront par exemple que : \[M(3000)_{F_2}=\frac{MUF(3000)_{F_2}}{f_{0_{F_2}}}\]

Explicitons ces notations :

• \(M(3000)_{F_2}\) : facteur de distance pour un bond de 3000 km réfléchi par la couche \(F_2\)

• \(MUF\) : Maximum Usuable Frequency (fréquence maximum utilisable)

• \(MUF(3000)_{F_2}\) : MUF pour un bond de 3000 km réfléchi par la couche \(F_2\)

L’enregistrement du temps de propagation en fonction de la fréquence est appelé ionogramme oblique. Sur un ionogramme réel, apparaissent les caractères généraux suivants :

– Plusieurs traces correspondant à plusieurs modes de propagation.

– À une fréquence donnée, il existe communément plus d’un rayon capable d’assurer la liaison, l’un appelé rayon bas et l’autre rayon haut pour lequel on peut observer un dédoublement correspondant aux rayons ordinaire et extraordinaire.

– Au-delà d’une certaine fréquence, aucun rayon n’est plus capable d’assurer la liaison. Il s’agit d’une fréquence limite.

Il n’existe pas de méthode analytique permettant d’obtenir le profil réel d’ionisation à partir de l’ionogramme oblique. Cependant, il est possible par l’utilisation de réseaux de courbes de transmission et d’approximations.

Le sondeur bistatique permet d’étendre le champ des investigations à des régions éloignées de l’émetteur. Toutefois, sa mise en œuvre est plus difficile que celle du sondeur zénithal, car le relevé des ionogrammes exige une synchronisation rigoureuse de l’émetteur et du récepteur, ce qui est compliqué compte-tenu de l’éloignement des stations.

2.3. Sondages par rétrodiffusion

La méthode de sondage par rétrodiffusion a été expérimentée pour la première fois par L. Silberstein.

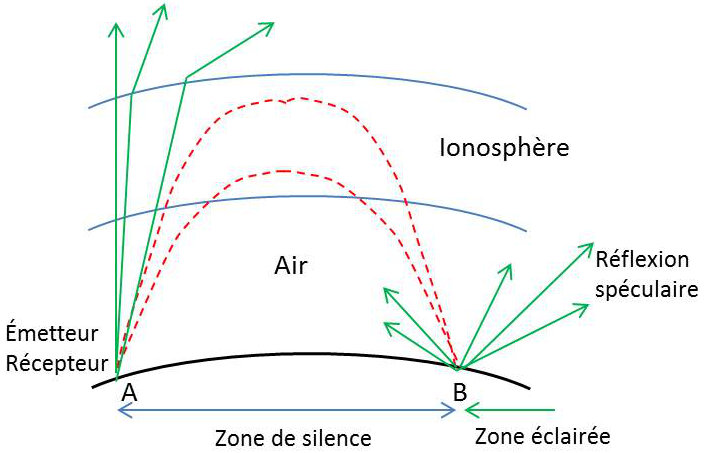
Elle utilise les propriétés diffusantes du sol, basée sur le principe du radar, le sol jouant le rôle de cible. Elle présente l’avantage de réunir en un même point A l’émetteur et le récepteur.

Dans les systèmes classiques, l’énergie est émise sous forme d’impulsions de courte durée.

La forme particulière du profil des couches produit une focalisation spatiale des rayons qui prend sa valeur maximum en un point B dont la position dépend à la fois de la fréquence d’émission et de l’ionosphère.

La plus grande partie de l’énergie est transmise dans la direction de la réflexion spéculaire, et peut donner lieu à des propagations multibonds. Une petite fraction de celle-ci est susceptible de retourner en A.

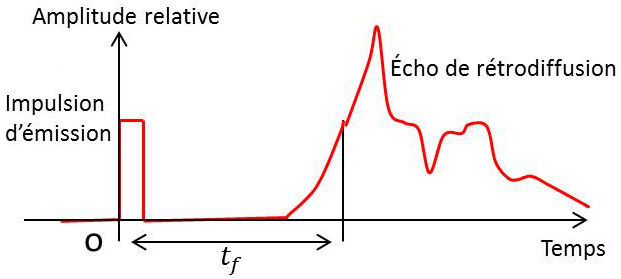La figure ci-contre représente le signal reçu, appelé écho de rétrodiffusion. Il est caractérisé par une rapide croissance de l’amplitude qui permet de définir un temps \(t_f\) appelé temps de focalisation, mesuré sur le front avant de l’écho.

La forme de l’écho, c’est-à-dire la variation de son amplitude en fonction du temps de propagation, est conditionnée par le profil d’ionisation, tandis que son amplitude est essentiellement déterminée par le sol.

L’enregistrement du temps de propagation en fonction de la fréquence d’émission s’appelle ionogramme de rétrodiffusion.

Il n’existe pas de méthode analytique permettant d’obtenir le profil d’ionisation à partir de l’ionogramme de rétrodiffusion. Cependant, il est possible, par l’utilisation de courbes de transmission de déduire de l’ionogramme de rétrodiffusion un ionogramme zénithal moyen donc un profil d’ionisation moyen.

Un sondeur à rétrodiffusion, équipé d’une antenne rotative, permet l’investigation de l’ionosphère dans toutes les directions, sur des distances atteignant couramment 3000 km. Néanmoins,jusqu’à présent, son utilisation a été très limitée à cause de deux points suivants :

– La diffusion introduit un affaiblissement considérable, de l’ordre de 100 dB, ce qui conduit dans les systèmes classiques à utiliser des puissances supérieures à 100 kW afin d’obtenir un rapport signal/bruit convenable.

– Contrairement à l’ionogramme oblique, l’ionogramme de rétrodiffusion ne donne pas la distance de bond, qui permettrait de lire directement la MUF, mais le temps de propagation qui n’est pas relié de façon simple à la distance atteinte.

Ces difficultés, liées à la nature même des sondages, expliquent que le procédé de rétrodiffusionne ne soit pratiquement pas utilisé pour la mesure systématique des paramètres ionosphériques.

3. Propagation ionosphérique et télécommunications

Les transmissions HF (entre 3 et 30 MHz) à travers le canal ionosphérique sont intéressantes, mais les systèmes doivent être adaptés au milieu à fluctuations non régulières. Les modems doivent être auto-adaptatifs. Les principales catégories de systèmes sont :

• les systèmes dans lesquels l’information est émise à cadence lente sur chaque sous-porteuse ;

• les systèmes auto-adaptatifs à correction partielle ou totale des distorsions du canal émises ;

• les systèmes utilisant des codes correcteurs d’erreurs.

Dans les premiers, plusieurs sous-porteuses dans la bande sont utilisées pour transmettre, avec une faible vitesse de modulation, les informations. Les largeurs de bande occupées par chaque signal élémentaire sont faibles d’où une bonne résistance aux brouillages. Ils sont sensibles au fading, mais efficaces pour combattre les effets liés à l’étalement de réponse impulsionnelle du canal.

Les systèmes auto-adaptatifs utilisent un filtre correcteur adapté aux caractéristiques du canal. Ce système corrige donc les effets des trajets multiples, mais la distorsion d’amplitude qui n’est pas corrigée laisse subsister une distorsion inter-symboles.

Dans les systèmes de transmission utilisant des codes bloc détectés par un critère à maximum de vraisemblance, le meilleur codage est celui où les inter-corrélations entre vecteurs sont minimales pour tous les décalages possibles.