1. Historique et introduction

Les premières fibres optiques ont été utilisées en médecine, sur le principe de la réflexion totale. Grâce au laser, source de lumière à la fois puissante, cohérente et directionnelle, la fibre optique est devenue le canal de transmission privilégié en télécommunications.

Ses principaux avantages :

• la faible atténuation permettant d’accroître la distance entre répéteurs ;

• l’insensibilité aux interférences électromagnétiques externes BF ;

• la large bande passante (débits importants) ;

• la réduction significative du nombre de stations d’amplification.

Deux inconvénients toutefois temporaires :

• le faible rendement dans les conversions optique \(\leftrightarrow\) électronique ;

• une certaine fragilité (mais actuelle).

2. Propagation, approche géométrique

2.1. Fibre à saut d’indice

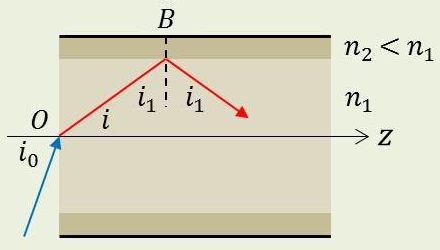Un cylindre de matériau transparent, homogène (indice \(n_1\) et diamètre \(2~a\)), le coeur, est entouré d’un milieu transparent, homogène (indice \(n_2<n_1\) et diamètre extérieur \(2~b\)), la gaine.

Un rayon lumineux issu d’un milieu d’indice \(n_0\) (exemple l’air) et faisant avec l’axe \(Oz\) de la fibre un angle \(i_0\) la pénètre en \(O\). Il est réfracté suivant un angle : \[i=\frac{\pi}{2}-i_1\qquad[1]\]

Le rayon lumineux suivra son guide tant que : \[\sin i_1 <~\frac{n_2}{n_1}\qquad[2]\]

Dans le cas de l’air (\(n_0=1\)) et d’après la loi de Snell : \[\sin i_0~\leq~\sqrt{n_1^2-n_2^2}\qquad[3]\]

Pour un faible écart relatif d’indice \(\Delta\) cœur / gaine : \[\Delta=\frac{n_1-n_2}{n_1}\quad;\quad n_1^2-n_2^2~\approx~2~n_1^2~\Delta\qquad[4]\]

Ne seront guidés que les rayons intérieurs à un cône de demi-angle au sommet tel que : \[ON=\sin i_{ON}=\sqrt{n_1^2-n_2^2}=n_1~\sqrt{\Delta}\qquad[5]\]

Une forte ouverture numérique \(ON\) autorise le couplage d’une quantité importante de lumière dans la fibre, un avantage pour les applications optiques en tant que telles. En télécommunications par contre, elle entraînerait une forte dispersion de temps de propagation entre les rayons. Un ordre de grandeur courant : \(0,3<ON<0,6\).

2.2. Fibre à gradient d’indice

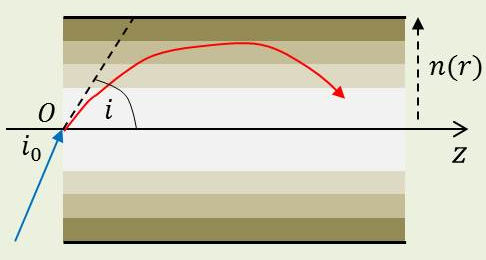La valeur d’indice décroît continument depuis l’axe jusqu’à l’interface : \[n(r)=n_1~\sqrt{1-2~\Delta~(r/a)^g}\qquad\text{avec~:}\quad g\approx 2\qquad[6]\]

Pour \(g=2\), la loi est dite parabolique.

Les rayons guidés sont ceux tangents à l’interface cœur – gaine pour \(i_0=i_{ON}\).

\[\left\{ \begin{aligned} ON(0)&=n_1~\sqrt{2~\Delta} && O\in[\text{axe}]\\ ON(r)&=ON(0)~\sqrt{1-(r/a)^g}\qquad && O\notin[\text{axe}] \end{aligned} \qquad[7] \right.\]

L’ouverture effective de la section droite d’entrée est : \[[ON]_{eff}=\frac{ON(0)}{\sqrt{2}}\qquad[8]\]

La puissance lumineuse nécessaire à la fibre à gradient d’indice pour être guidée est la moitié de celle nécessaire à la fibre à saut d’indice.

3. Propagation, approche électromagnétique

3.1. Équations de propagation

La propagation (approche par modes) est régie par les équations de Helmholtz : \[\left\{ \begin{aligned} \Delta E-\mu_0~\varepsilon_i~\frac{\partial^2E}{\partial t^2}&=0\\ \Delta H-\mu_0~\varepsilon_i~\frac{\partial^2H}{\partial t^2}&=0 \end{aligned} \qquad i=1,~2\qquad[9] \right.\]

En régime harmonique (pulsation \(\omega\)), en coordonnées cylindriques (\(r,~\varphi,~z\)) et du fait de la symétrie axiale, les solutions sont exprimées au moyen des fonctions de Bessel \(J_p(\nu)\).

3.2. Régimes monomode et multimode

1) La condition de régime monomode est donnée par : \[\lambda>\lambda_c=\frac{2\pi~a~n_1}{2,405}~\sqrt{2~\Delta}\quad;\quad\lambda_c\text{ : coupure}\qquad[10]\]

Le diamètre de cœur des fibres monomodes est de l’ordre de 10 mm, grandeur proche de de la longueur d’onde de la lumière qui se propage.

Le nombre de modes guidés, entier fini, peut être approché par la formule : \[N=\frac{\nu^2}{2}\qquad[11]\]

\(N\) peut être de l’ordre de quelques milliers.

2) Le diamètre des fibres multimodes est plus important, de l’ordre de 50 à 85 µm.

Pour une fibre à gradient d’indice, la condition de propagation à mode guidé unique est donnée par : \[\nu<\nu_c=2,405~\sqrt{1+\frac{2}{g}}\qquad[12]\]

Dans le cas du profil parabolique : \(\nu_c=3,401\).

4. Dispersion

4.1. Dispersion intermodale

Tous les rayons n’ont ni le même trajet ni la même vitesse de propagation ; c’est la principale cause de dispersion. Une impulsion lumineuse injectée dans la fibre va s’élargir. Deux impulsions successives, bien distinctes à l’entrée de la fibre pourront interférer, d’où une perte d’information.

1) Pour les fibres à saut d’indice, le temps de propagation a pour expression : \[t(i)=\frac{L~n_1}{c~\cos i}\qquad[13]\]

• \(L\) : longueur de la fibre

• \(c\) : vitesse de la lumière

La dispersion intermodale est l’écart entre les valeurs extrêmes de \(t(i)\) par unité de longueur : \[\Delta t_{im}=\frac{t(i_M)-t(0)}{L}=\frac{n_1}{c}~\Delta=\frac{ON^2}{2~c~n_1}\qquad[14]\]

• \(i_M\) : inclinaison maximale

2) Pour les fibres à gradient d’indice, on obtient pour les rayons méridiens \[t(i)=\frac{L~n_1}{c~\cos i}~\Big\{1-\frac{2-P}{g+2}~\sin^2 i\Big\}\qquad[15]\]

• \(P\) : paramètre de dispersion de profil (dépend du matériau et de la longueur d’onde)

Les fibres monomodes ne subissent pas de dispersion intermodale, d’où leur intérêt dans les transmissions à longue distance.

4.2. Dispersion intramodale ou chromatique

La dispersion intramodale ou chromatique se produit pour chaque mode, même pour une fibre monomode, si, aux extrémités de la bande couverte par la source modulée, les vitesses de groupe ne sont pas égales.

La valeur d’élargissement d’impulsion par unité de longueur vaut : \[\Delta t_c=(D_M+D_G)~\Delta\lambda\qquad[15]\]

• \(\Delta\lambda\) : largeur spectrale de la source

• \(D_M\) : dispersion due au matériau

• \(D_G\) : dispersion due au guide

La deuxième est négligeable pour les fibres multimodes, sauf lorsqu’il s’agit de modes proches de la coupure.

4.3. Dispersion totale

Statistiquement, les deux dispersions se présentent comme deux distributions indépendantes (distribution entre plusieurs modes et entre plusieurs longueurs d’onde).

La dispersion totale s’écrit : \[\Delta t=\sqrt{\Delta t_{IM}^2+\Delta t_c^2}\qquad[16]\]

Cependant, dans les fibres monomodes, une compensation de la dispersion guidée (négative) par la dispersion matériau peut se produire.

5. Atténuation

5.1. Diffusion et absorption

L’énergie transportée par l’onde optique subit une atténuation attribuable à deux phénomènes physiques dans le matériau : la diffusion et l’absorption.

Quand la lumière rencontre une irrégularité de dimension inférieure à sa longueur d’onde, elle est diffusée (diffusion de Rayleigh). Certaines des directions de diffusion sont telles que les conditions de réflexion totale à l’interface cœur – gaine ne sont plus remplies : une partie de la lumière entre dans la gaine pour y être perdue.

L’atténuation due à Rayleigh est proportionnelle à \(\lambda^{-4}\), ce qui nous conduit à travailler à des longueurs d’onde élevées (infra-rouge).

L’absorption de la lumière se produit chaque fois qu’un photon entrant en action avec un atome, une molécule ou un solide a suffisamment d’énergie pour induire une transition électronique.

Il existe trois types d’absorption : deux intrinsèques et une extrinsèque :

1. absorptions intrinsèques :

   – Un photon induit une transition électronique entre des bandes d’énergie situées dans la bande UV et que les fibres en silice ne transmettent pas. La largeur de bande interdite du verre, qui est un isolant, est grande.

   – L’onde électromagnétique excite les vibrations moléculaires de la silice, qui présentent un spectre complexe dans l’infra-rouge (nombreux pics entre 2 et 25 µm). L’atténuation augmente rapidement quand la longueur d’onde dépasse 1,7 µm.

2. absorption extrinsèque :

   – Les impuretés, ions de métaux de transition et ions \(OH\) provenant des traces d’eau. Le plus important pic d’absorption est dû aux liaisons \(OH\) pour la longueur d’onde 1,3 µm. Une teneur en eau résiduelle de l’ordre de \(10^{-7}\) est nécessaire pour ne pas être gêné par ce pic.

5.2. Autres phénomènes

Lorsqu’on raccorde bout à bout deux fibres optiques, il apparaît des pertes ponctuelles dues à la réflexion de Fresnel aux deux interfaces verre – air, à la différence entre les paramètres des deux fibres et au positionnement relatif non correct.

Il y a aussi les pertes par courbure et micro-courbures. À l’entrée d’une section courbée, il y a augmentation de l’angle \(i\) du rayon à l’interface cœur – gaine. Les modes d’ordre élevé sont alors réfractés. L’atténuation des modes d’ordre plus faible augmente par couplage avec les modes réfractés.

Il en est de même pour une déformation locale de l’interface sous l’effet d’une contrainte, l’axe restant rectiligne. On parle alors de micro-courbure.

5.3. Fenêtres de transmission

Compte tenu des courbes d’atténuation et de dispersion chromatique, ainsi que des composants optoélectroniques actuellement disponibles, on définit trois fenêtres de transmission :

1. 0,8 µm \(<\lambda<\) 0,9 µm : ne correspond pas à un minimum d’atténuation (\(\alpha=\) 2 à 3 dB/km) ou de dispersion, mais à l’optimum d’utilisation des matériaux les mieux maîtrisés (Si et GaAs) ;

2. \(\lambda=\) 1,3 µm : correspond à un minimum relatif d’atténuation (\(\alpha=\) 0,4 à 0,5 dB/km) et au minimum de la dispersion chromatique ;

3. \(\lambda=\) 1,55 µm : correspond au minimum absolu d’atténuation (\(\alpha=\) 0,15 à 0,2 dB/km). Il est très difficile d’annuler ici la dispersion chromatique (\(\lambda>\) 1,37 µm) et les composants ont un coût élevé.

6. Sources bibliographiques

• Theory of Dielectric Optical Waveguide Quantum Electronics
  D. Marcuse (Academic Press, 1974)

• Light Transmission Optics
  D. Marcuse (Van Nostrand, 1982)

• Les fibres optiques. Introduction aux télécommunications
  J.P. Nerou (Le Griffon d’argile inc, 1983)

• L’optique guidée monomode et ses applications
  J.P. Nerou (Masson, 1985)

• Les systèmes à fibres optiques
  P. Halley (Eyrolles, 1985)

• Principles of Modern Optical Systems
  I. Andonovic, D. Uttamchandani (Artech House, 1989)

• An Introduction to Fiber Optics Sustem Design
  B.E. Briley (North Holland, 1990)

• Télécommunications optiques
  P. Lecoy (Hermes, 1992)

• Les télécommunications
  F. Du Castel (X.A. Descours Berger-Levrault International, 1993)