1. Transducteur et capteur. Définitions et spécificités

Capteur et transducteur sont deux choses bien distinctes, sachant toutefois qu’un transducteur comporte toujours un capteur :

• Le transducteur est le système électronique qui convertit un phénomène physique en courant ou tension électriques.

• Le capteur est le dispositif qui transforme l’état d’une grandeur physique observée en une grandeur utilisable : tension électrique ou intensité, déviation d’une aiguille. . .

Le capteur (en anglais sensor) est le moyen technique qui permet de sonder l’environnement. Un environnement qui peut être caractérisé par des paramètres physiques d’origines diverses : lumière, température, force, pression, flux liquide ou gaz, résistance électrique, etc. Ces paramètres sont à l’origine d’une modification de l’état de sortie du capteur, par variation mais souvent par simple présence. On parlera d’ailleurs de capteurs de présence (surveillance).

Le capteur est l’élément d’un système électronique de détection (ou d’acquisition de données) qui fait l’interface entre le processus physique, en tant que tel, et l’information utile qui en résulte.

Le cas le plus intéressant (pour être le plus pratique) est celui du capteur linéaire : la caractéristique du signal de sortie est proportionnelle au paramètre d’action.

Capteur passif et capteur actif

Un capteur passif produit sa propre énergie (ou bien la récupère à partir du phénomène observé). C’est le cas du thermocouple pour une mesure de température.

À l’inverse, la présence d’une source externe de puissance (alternative ou continue) est nécessaire au fonctionnement du capteur actif. Sans cette source, aucun signal ne peut apparaître en sortie.

2. Matériaux pour capteurs

2.1. Transformation des déformations

2.1.1. Piézorésistance

Une déformation (d’ordre géométrique ou d’ordre électronique) peut être à l’origine d’un changement de conductivité électrique. Examinons chacune des deux possibilités :

1) Modification des propriétés géométriques

Un cas simple est celui du conducteur filaire soumis à une traction (étirement). On observera une variation relative de résistance : \[\frac{\Delta R}{R}=K_j~\frac{\Delta L}{L}\]

Le coefficient de proportionnalité \(K_j\) est appelé facteur de jauge.

2) Modification des propriétés électroniques.

Ce sont les contraintes subies par un cristal (cas des matériaux semi-conducteurs). La contrainte est bidimensionnelle : on définit deux coefficients, dits de piézorésistance :

• un coefficient longitudinal (parallèle à la déformation) : \(F_l\)

• un coefficient transversal (orthogonal à la déformation) : \(F_t\)

\[F_L=\frac{1}{P}~\Big(\frac{d\rho}{\rho}\Big)_{long}\quad;\quad F_T=\frac{1}{P}~\Big(\frac{d\rho}{\rho}\Big)_{trans}\]

\(P\) est la pression unilatérale appliquée. Cette pression est comptée positivement pour une compression.

2.1.2. Piézoélectricité

Sous l’action d’une contrainte mécanique, certains matériaux peuvent se polariser électriquement. C’est ce que l’on appelle l’effet piézoélectrique direct.

Son utilisation est très courante. C’est le cas de l’allume-gaz (production d’une étincelle) et celui de la lampe de poche (production temporaire d’un courant d’éclairage par l’ampoule).

De manière réciproque, ces matériaux peuvent se déformer sous l’action d’un champ électrique. Il s’agit de l’effet piézoélectrique inverse.

Matériaux piézoélectriques

L’effet piézoélectrique se rencontre dans deux types de matériaux :

• les corps piézoélectriques intrinsèques ;

• les corps ferroélectriques.

Pour les premiers, la propriété disparaît au-dessus d’une certaine température de l’ordre de plusieurs centaines de degrés Celsius (température de Curie). Le phénomène est réversible, c’est-à-dire qu’il réapparaît au retour à une température plus basse.

Pour les seconds, il se produit un phénomène d’hystérésis : ces corps ayant été préalablement polarisés par un champ électrique extérieur (de l’ordre du kV/mm), il se crée une polarisation rémanente qui entretient la propriété de piézoélectricité.

Note écologique rapportée au texte d’origine

Une concurrence du panneau solaire. Le développement original de pavés la société Pavegen sur une idée de son fondateur Laurence Kemball-Cook.

Chaque personne qui marche sur l’un de ces pavés génère entre 4 et 7 watts en fonction de son poids. Les dalles constituées de pneus de camions et de béton recyclés convertissent en électricité l’énergie apportée par les mouvements de pieds. Une énergie transformée en électricité qui peut être stockée.

Ce concept a été utilisé à Londres (2008) dans le premier « éco-nightclub » alimenté par les trépidations de ses clients. Il a été repris par une start-up israélienne (2010) pour être testé sur un tronçon d’autoroute à Haïfa et actuellement aux USA pour une autoroute californienne.

2.2. Transformations de champs électriques

Le principe du phénomène piézoélectrique repose sur l’existence des forces de Lorentz (sur une charge mobile placée dans une induction magnétique) : \[\overrightarrow{F}=e~(\overrightarrow{v}\wedge\overrightarrow{B})\]

• \(e\) : charge de l’électron

• \(v\) : vitesse de l’électron

• \(B\) : induction magnétique

Le tenseur de conductivité (corps conducteur ou semi conducteurs) s’en trouve modifié. Un exemple classique est celui de l’effet de Hall.

2.2.1. Principe de l’effet de Hall (1879)

Un courant traverse un barreau conducteur ou semi-conducteur. Un champ d’induction \(B\) est appliqué perpendiculairement au sens de passage du courant. Une tension (de Hall) apparaît alors sur les faces latérales du barreau. Cette tension est proportionnelle au champ magnétique et au courant, donc à la vitesse de déplacement des porteurs de charge.

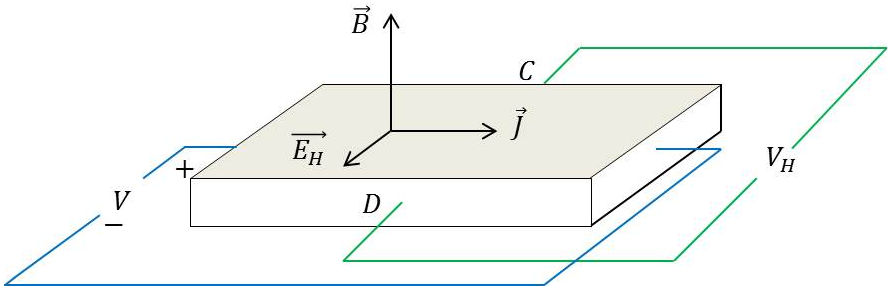Expression du champ de Hall : \[\overrightarrow{E_H}=\mu~(\overrightarrow{B}\wedge\overrightarrow{E_H})\]

• \(\mu\) : mobilité des porteurs

• \(B\) : induction magnétique

• \(E_H\) : champ électrique appliqué

2.2.2. Caractérisation de l’effet de Hall

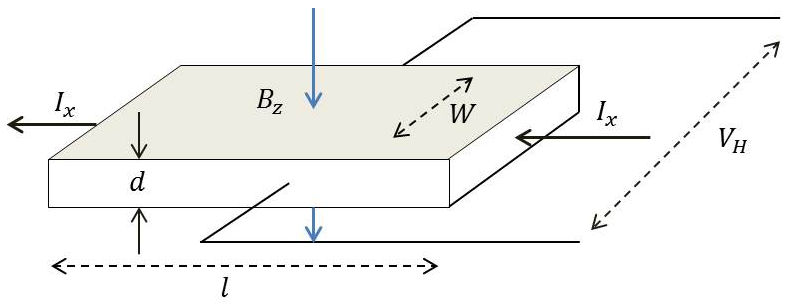Du fait de la force de Lorentz les lignes de courant sont déviées d’un angle \(\alpha_H\), d’où la présence de charges (positives et négatives) de chaque côté du matériau.

Apparition d’un champ électrique et d’une tension (dits de Hall) : \[\begin{aligned} E_H&=v_x~B_z\\ V_H&=E_H~W=v_x~B_z~W \end{aligned}\]

Introduisant le courant de mouvement des électrons, on démontre que : \[V_H=R_H~\frac{I_x~B_z}{d}\]

\(R_H\) est le coefficient de Hall.

L’angle de flexion \(\alpha_H\) peut être calculé à partir des composantes \(E_x\) et \(E_y\) des champs électriques (champ d’origine et champ par effet Hall)

2.3. Transformation de l’énergie lumineuse

À un rayonnement électromagnétique de fréquence \(\nu\) est associé un quantum d’énergie \(\hbar~\nu\). Si cette énergie est suffisamment élevée, des paires électrons – trous sont créés. Ces porteurs générés induisent une modification des propriétés électriques macroscopiques :

1. Effet photorésistance : la résistivité électrique du matériau diminue sous l’effet d’un rayonnement électrique de quantum énergétique suffisamment élevé.

2. Effet photovoltaïque : une tension apparaît aux bornes du semiconducteur et peut atteindre des valeurs de l’ordre de quelques dixièmes de volts, même pour les semiconducteurs usuels.

3. Effet photodiode : le courant généré augmente proportionnellement au flux lumineux incident.

3. Les trois modes de capture (R, L, C)

3.1. Effet résistance

Il s’agit d’un effet piézoélectrique. Suivant étirement ou compression (\(\pm\)), la résistance a pour expression : \[R=R_0\pm\Delta R=\frac{L_0\pm\Delta L}{S_0\pm\Delta S}\]

\(S\) : section du fil (à priori cylindrique)

On démontre que la variation relative de résistance est de la forme : \[\frac{\Delta R}{R}=\frac{\Delta\rho}{\rho}+(1+2~\eta)~\frac{\Delta L}{L}\]

\(\eta\) : coefficient de Poisson

Les montages classiques sont réalisés à partir de ponts diviseurs ou de ponts de Wheatstone équilibrés quand le système est au repos.

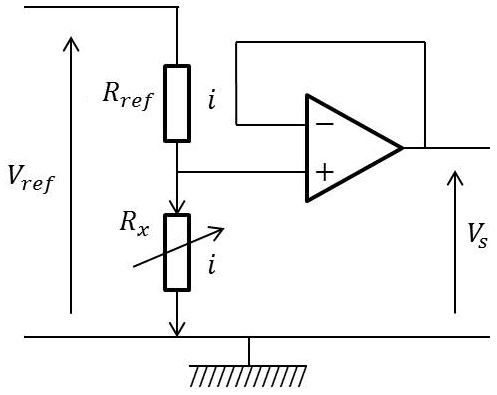Le cas le plus simple est celui du diviseur de tension, avec une résistance fixe \(R_{ref}\) et la résistance de jauge \(R_x\) : \[R_x=R_0~(1+x)\]

• \(R_0\) : valeur initiale de la résistance

• \(x\) : variation due à l’action à mesurer (sa valeur est de l’ordre de quelques pour-cents)

Expression de la tension de sortie : \[V_s=\frac{R_x}{R_x+R_{ref}}~V_{ref}\]

3.2. Effet inductance

Le principe repose sur la relation classique : \[L=N~\frac{d\Phi}{di}\]

• \(L\) : autoinductance de la bobine

• \(N\) : nombre de spires de la bobine

• \(\Phi\) : flux traversant la bobine

• \(i\) : courant de cette bobine

En introduisant la force magnétomotrice (\(f_m\)) et la réluctance (\(R_L\)) : \[f_m=N~i\quad;\quad R_L=\frac{f_m}{\Phi}\]

on obtient (calcul élémentaire) : \[L=\frac{N^2}{R_L}\]

L’effet capteur est obtenu en modifiant la reluctance : en longueur, en perméabilité ou bien suite à un déplacement.

Exemple : capteur à pont de Wheatstone

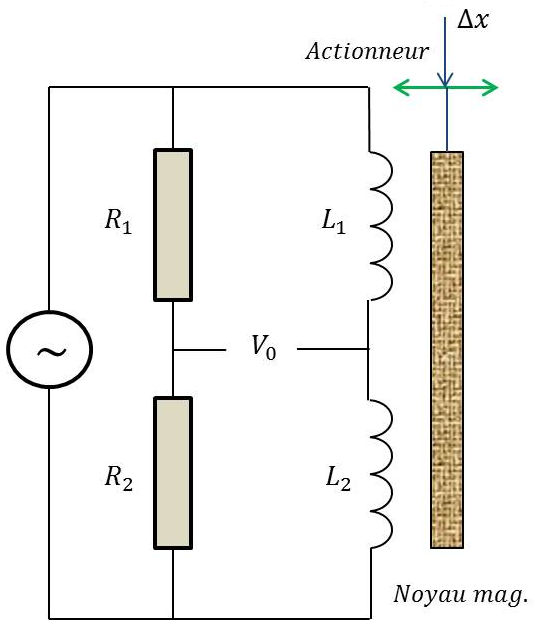Les réactances des bobines sont fonction de l’excitation alternative appliquée.

Au repos (disposition symétrique du noyau magnétique), les inductances sont égales ainsi que leurs réactances et le pont est équilibré : \[\frac{R_1}{R_2}=\frac{X_{L1}}{X_{L2}}\quad\Rightarrow\quad V_0=0\]

Dès que le noyau est en mouvement, la tension de sortie est modifiée. D’où une modification des inductances, donc des réactances.

3.3. Effet capacitance

Les montages sont des transpositions de montages de base avec résistances (résistances simulées par commutation de capacités).

Les variations de capacité peuvent résulter d’une modification du diélectrique ou de la géométrie de la capacité. On peut supposer que celle-ci est due à un mouvement d’une des électrodes.

Partons de l’expression de la capacité, par exemple d’un condensateur plan : \[C=\varepsilon~\frac{S}{e}\quad;\quad\varepsilon=\varepsilon_0~\varepsilon_r\]

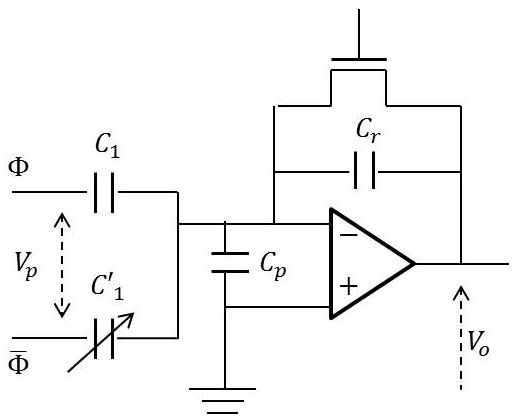En désignant par \(w(x,~y)\) le déplacement pour chaque point \((x,~y\)) de cette électrode, cette variation peut être exprimée par (condensateur plan) : \[\Delta C=C_0-\iint\frac{\varepsilon}{e-w(x,~y)}~dx~dy\]

Les capteurs de pression ou les accéléromètres sont généralement conçus sur ce principe.

Le montage est analogue à celui du potentiomètre précédent mais avec des capacités, à priori des capacités commutés (\(C_1\) et \(C'_1\)).

\(\Phi\) (et \(\overline{\Phi}\)) désigne la phase de charge de la capacité.

Un effet de pompage est créé entre la capacité de référence \(C_r\) et celle du capteur \(C_p\) dont la valeur nominale est à la référence.

La différence de charge, proportionnelle à la différence de capacité, est intégrée pour produire une tension dont la sortie est proportionnelle à cet écart, mais divisée par une capacité de réaction (feedback).

4. Modélisation et paramètres caractéristiques

4.1. Équations de fonctionnement

Un capteur est un système recevant un signal \(x(t)\) et restituant un signal \(y(t)\).

Il existe deux types de capteurs :

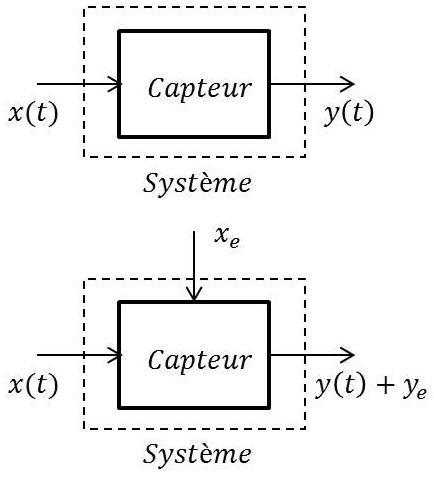1) Les capteurs pour lesquels l’énergie de sortie est prélevée uniquement sur celle du signal d’entrée.

L’équation de fonctionnement est de la forme : \[y(t)=F\{x(t)\}\]

2) Les capteurs pour lesquels la source d’énergie est externe. Le signal introduit (additif) pourra être stationnaire (courant ou tension de commande) ou bien un bruit.

En introduisant l’action de la source externe : \[y(t)=F\{x(t)+x_e(t)\}\]

Dans un capteur idéal, le signal de sortie est proportionnel au signal d’entrée : \[y(t)=K~x(t)\]

relation encore valable avec un capteur à source externe, mais à la translation \(x_e\) près.

Supposant les paramètres dépendant linéairement du temps, la relation généralisée est une expression différentielle à coefficients constants de la forme : \[a_n~\frac{d_ny}{dt^n}+\dots+a_1~\frac{d_y}{dt}+a_0~y=x(t)\]

5. Paramètres caractéristiques

Dans la pratique, les paramètres les plus importants sont :

– Le gain : \[A=\frac{y}{x}\]

– La sensibilité : \[\sigma=\frac{dy}{dx}\]

– La réponse : \[\Delta y(t)=y(t)-y_e\]

Pour prendre l’exemple (assez fréquent) des systèmes du premier ordre :

\[a_1~\frac{dy}{dt}+a_0~y=x(t)\]

On peut associer au système une fonction de transfert (de Laplace) : \[H(p)=\mathcal{L}\Big\{\frac{y(t)}{x(t)}\Big\}\]

– La constante de temps appliquée au système, et correspondant à 90 % du temps nécessaire à la stabilisation signal de sortie : \[\tau=\cfrac{a_1}{a_0}\]

Exemple tension échelon \(U\) appliquée au système et réponse :

\[\begin{aligned} y(t)&=\frac{U}{a_0}~\Big\{1-\exp\Big(-\frac{t}{\tau}\Big)\Big\}+y_e \\ \Delta y(t)&=\frac{U}{a_0}~\Big\{1-\exp\Big(-\frac{t}{\tau}\Big)\Big\}\end{aligned}\]