1. Historique et contexte

Dès le lancement du Plan Calcul, sous le gouvernement M. Debré (1966), le développement rapide de l’informatique et de ses applications dans les années 60, l’ordinateur s’est imposé dans les applications de la théorie des circuits des réseaux électroniques, en particulier le filtrage.

Dès cette époque, l’étude d’un modèle mathématique au moyen de l’ordinateur, appelée simulation, l’analyse numérique et l’algorithmique sont devenues incontournables. Physiquement, le modèle, le plus simple dans les limites du possible, doit être obligatoirement le moins éloigné des réalités à venir, car il convient de tout connaître des comportements physiques, et des grandeurs, utiles et secondaires, pour mieux les exprimer.

Tout l’art du bon physicien doublé du bon analyste programmeur : le calcul du filtre sur ordinateur est la première phase du processus de conception : C.A.D. (Computer Aided Design), devenu C.A.O. (conception assistée par ordinateur) en français.

1.1. Analyse et synthèse

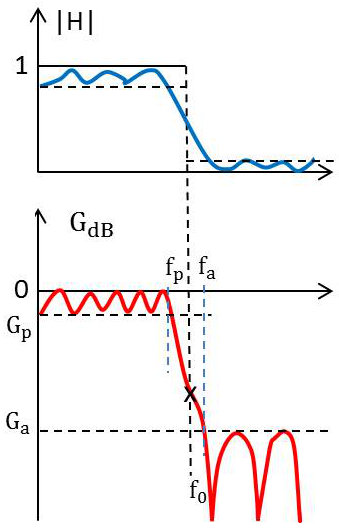
Analyser un réseau, c’est simuler son fonctionnement, la structure (modèle) et les valeurs des composants étant connues. On détermine en plusieurs points, suivant un pas donné, les valeurs de sa réponse harmonique (module de la fonction de transfert) ou plus particulièrement le gain \(G_{dB}\) (ou l’atténuation \(A_{dB}\)) dans l’échelle logarithmique classique.

Dans certains cas, il peut être intéressant de connaître son comportement en phase (argument de la fonction de transfert) et éventuellement celui du temps de retard de groupe (dérivée de la phase par rapport à la pulsation \(\omega=2\pi~f\)).

Synthétiser un réseau, c’est opération inverse. C’est rechercher la forme et l’expression d’une fonction de transfert appropriée, c’est trouver une structure électronique appropriée et c’est enfin déterminer la valeur des composants en associant la structure et la fonction de transfert.

Ceci en vue d’obtenir des caractéristiques définies à l’avance et exprimée par un gabarit d’atténuation en fonction de la fréquence, limites entre lesquelles le graphe de l’atténuation correspondant à la fonction de transfert devra s’inscrire.

1.2. Filtre idéal et formes approchées

1.2.1. Boutade

Un de mes directeurs techniques à Thomson-CSF m’avait fait un jour une remarque amusante. Il comparait la forme d’une réponse réelle à celle d’une corde suspendue à un étendoir à linge au moyen d’une ou plusieurs pinces à linge. Du nombre et de la répartition de ces pinces dans la bande passante dépendait la qualité de l’approximation du 1 dans la bande passante, l’existence d’ondulations plus ou moins régulières et de l’aspect plus ou moins abrupte de la corde une fois passée la bande passante.

De quoi mettre en colère le mathématicien fanatique de l’approximation (par ondulations plus moins amples) au sens de Chebycheff en analyse numérique. C’est ce que m’inspirent, avec le recul et malgré moi, les schémas qui suivent.

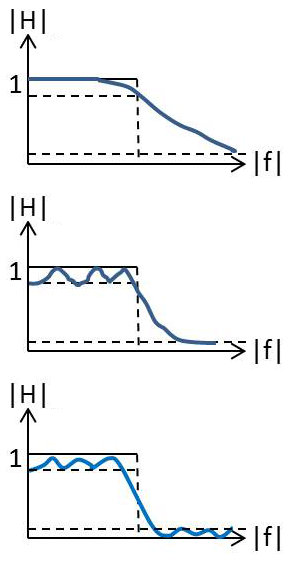Le point de départ est du domaine des mathématiques pures, puis de l’algorithmique. Le problème de l’approximation consiste, grâce à une fonction pressentie, à approcher au mieux la réponse harmonique du filtre idéal en créneau (c’est-à-dire théorique).

Les bandes passante et non passante sont en fait séparées par une bande de transition (ici non matérialisée), plus ou moins large en fonction de la raideur attendue pour le filtrage, donc pour la sélection optimale des fréquences. Comme nous le verrons sous peu cette contrainte d’obliquité est conforme au respect des conditions exigées pour que le filtre soit physiquement réalisable.

Dans les deux premiers cas, on observe que les zéros de transmission sont envoyés à l’infini de manière quasi-asymptotique. L’approximation adoptée pouvant présenter ou non des ondulations dans la bande passante. Dans le troisième cas, on observe la présence de zéros de transmission hors bande passante (bande atténuée), mais, par la même occasion, une raideur plus importante dans la bande de transition. Approximation la plus voisine du filtre idéal.

Mon directeur technique l’aurait justifiée, avec un petit sourire, par la présence de pinces à linge dans la bande atténuée.

2. Approximation et fonction de transfert. Conditions

2.1. Conditions de réalisabilité

La caractéristique première d’un filtre, quelle que soit la technologie adoptée, est sa fonction de transfert, c’est-à-dire le rapport de la tension de sortie \(V_s\) à la tension d’entrée \(V_s\). Son expression se présente généralement comme la fraction de deux polynômes : \[H(p)=\frac{Q(p)}{E(p)}\qquad p=j\omega\quad\text{variable de Laplace unilatérale}\]

Le polynôme \(Q(p)\) peut être réduit à une constante (cas des filtres dits polynômiaux).

Les coefficients des polynômes \(Q(p)\) et \(E(p)\) doivent être réels. De plus, pour des raisons de stabilité, les zéros du polynôme dénominateur \(E(p)\) doivent avoir une partie réelle négative. Telles sont les conditions de Hurwitz.

Il résulte de ces deux propositions, une disposition elliptique dans le plan complexe des "zéros" de : \[H~\overline{H}=H(p)~H(-p)=H(j\omega)~H(-j\omega)=0\]

avec une double symétrie dite quadrantale (figure ci-contre).

Après l’artifice mathématique de calcul (\(H~\overline{H}\)), les zéros physiques à retenir sont ceux du demi-plan gauche de stabilité du plan complexe.

Dans le cas de l’approximation polynomiale de type Butterworth, la répartition sera particulière (circulaire puisqu’il s’agira des racines complexes de l’unité).

2.2. Notion de gabarit

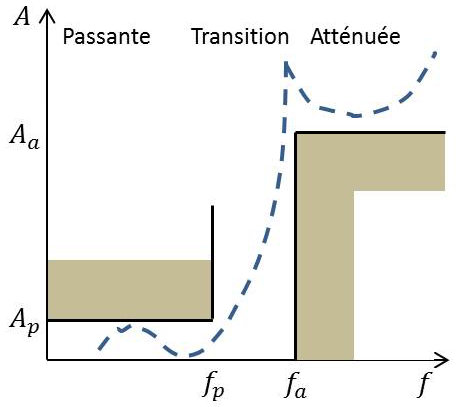Dans sa sélection de bandes de fréquences, le spécialiste du filtrage se définit le plus souvent un gabarit d’affaiblissement ou d’atténuation \(A_{dB}(f)\). C’est la représentation inversée du gabarit de gain \(G_{dB}(f)\), plus pratique du fait d’un affichage de valeurs positives.

Nous faisons ici l’hypothèse du filtre dit à large bande. Les filtres dits à bande étroite (filtre sélectif ou le filtre réjecteur), plus simples à traiter, feront l’objet d’un paragraphe particulier.

Notons que l’affaiblissement ou l’atténuation, mesurés en \(dB\) sont exprimés par la relation : \[A=20~\log_{10}|H(j\omega)|=10~\log_{10}[H(j\omega)~H(-j\omega)]\qquad;\qquad\omega=2\pi~f\]

Remarque 1 : Multiplicité de solutions

Il existe naturellement un grand nombre de solutions \(H(p)\) suivant le type d’approximation mathématique choisie et suivant l’exigence d’insertion de la courbe dans le gabarit (courbe centrée au mieux ou tangente aux contraintes), c’est-à-dire le degré du ou des polynômes de \(H(p)\) ou encore l’ordre du filtre.

Remarque 2 : Filtres non passe-bas

Notre étude portera uniquement sur les approximations relatives aux filtres passe-bas (large bande), les seuls aux algorithmes mathématiques connus.

Pour les autres types de filtres à bande large (passe-haut, passe-bande et coupe-bande), des transformations de fréquence permettent de se placer dans les conditions intermédiaires. Le gabarit est transformé en gabarit de filtre passe-bas appelé alors prototype. On revient ensuite au filtre original en appliquant la transformation de fréquence inverse.

2.3. Formes analytiques de la fonction de transfert

Le module de la fonction de transfert étant inférieur à l’unité, il est logique de la présenter sous la forme générale suivante : \[|H(p)|^2=\frac{1}{1+\varepsilon^2~|\Phi(p)|^2}\]

\(\varepsilon\), appelé facteur de forme, est lié à la coupure \(\{f_p,~A_p\}\) par la relation : \[\varepsilon^2=10^{Ap/10}-1\qquad;\qquad \varepsilon^2=1~~\text{pour}~~A_p=3~dB\]

La fonction \(\Phi\), mise en évidence au dénominateur de la fonction \(H\), porte le nom de fonction caractéristique.

On distingue deux types de filtres :

– Les filtres polynômiaux dans lesquels \(\Phi(p)\) est un polynôme : \[\Phi(p)=\sum_{k=1}^{n+1} a_k~p^{k-1}\]

C’est le cas des filtres de Butterworth, Chebycheff, Bessel et Papoulis.

– Les filtres elliptiques dans lesquels \(\Phi(p)\) est une fraction rationnelle : \[\Phi(p)=p^r\frac{\Pi_{i=1}^n~(p^2+a_i^2)}{\Pi_{i=k}^m~(p^2+b_k^2)}\]

L’exemple type est celui des filtres de Cauer.

3. Algorithmes d’approximation

3.1. Approximations polynômiales (passe-bas)

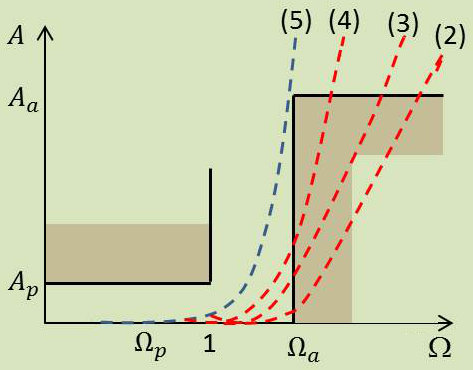
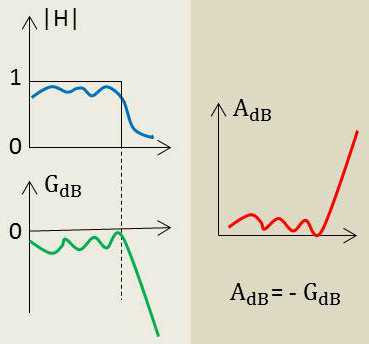Le but théorique de toute approximation est de trouver une fonction mathématique qui permettra de coller au mieux au créneau qui est la forme idéale.

En bande passante, c’est la valeur 1 qui est approchée au mieux, avec ou sans ondulation. Hors bande passante, ce sera la valeur asymptotique 0 : \[|H|\rightarrow 0\qquad\text{donc un gain}\quad G_{dB}=20~\log_{10}|H|\rightarrow-\infty\]

Les zéros de transmission sont envoyés à l’infini.

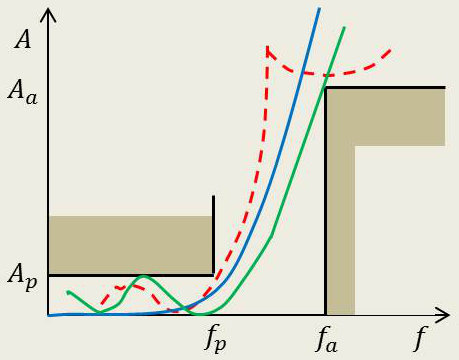Examinons, figure ci-contre le gabarit en atténuation et les trois graphes qui y sont inscrits :

Deux approximations sont de type polynômial :

• la bleue, à bande passante plate, est une approximation par polynôme de Bessel, Butterworth ou Papoulis ;

• la verte, à bande passante ondulée, est une approximation par polynôme de Chebycheff.

En bande atténuée et dans tous les cas, une direction asymptotique vers l’infini.

Une approximation de type elliptique (rouge pointillé). On remarque :

• une ondulation dans la bande passante,

• une forte raideur dans la bande de transition,

• des pointes d’atténuations infinies en bande atténuée,

• des remontées (à niveau égal) entre les points critiques.

Pour la commodité des calculs, nous introduisons la fréquence normalisée : \[\Omega=\frac{\omega}{\omega_0}=\frac{f}{f_0}\]

Dans le cas du filtre passe-bas polynômial, la fréquence de normalisation \(f_0\) s’identifie avec \(f_p\), fréquence de coupure du filtre. Dans le cas du filtre de Cauer, très particulier, cette fréquence sera \(f_0=\sqrt{f_p~f_a}\), moyenne géométrique entre les fréquences de coupure \(f_p\) et d’atténuation \(f_a\).

L’ordre \(n\) du filtre (nombre d’éléments) est aussi celui du polynôme. Plus \(n\) est grand, plus la raideur du filtre est importante dans la bande de transition.

Dans un système de calcul entièrement automatisé, cet ordre est généralement déterminé par approximations successives (calcul de \(A\) au point \(f\) correspondant à \(A_a\) de façon à ce que le graphe s’insère au mieux mais raisonnablement dans les contours du gabarit. Il existe cependant des réseaux d’abaques permettant de connaître graphiquement et immédiatement la valeur de cet ordre du filtre.

3.1.1. Polynôme de Butterworth

Les racines complexes de l’unité sont les génératrices du polynôme de Butterworth.

La fonction de transfert \(H(p)\) est telle que : \[|H(j\Omega)|^2=\frac{1}{1+\varepsilon^2~(-1)^n~\Omega^{2n}}\]

\(\Omega\) : fréquence normalisée ; \(n\) : ordre du filtre.

Pour déterminer l’ordre du filtre, on procède par itérations sur \(n\) (à partir de \(n=2\)), sur la relation : \[A(\Omega)=10~\log_{10}\{1+\varepsilon^2~(-1)^n~\Omega^{2n}\}\]

Ceci jusqu’à ce que : \[A(\Omega_a)\geq A_a\]

Dans le cas présent, la valeur \(n=5\) convient.

L’expression du polynôme \(E(p)\), dénominateur de \(H(p)\), est établie à partir de la position des racines 2 n-ième de l’unité réparties en symétrie quadrantale (\(E~\overline{E}=0\)), en ne retenant que les racines à partie réelle négative (critère de stabilité), associées deux à deux par couples conjugués.

Naturellement, pour un ordre impair, il existe une unique racine (\(\Omega=-1\)) sur l’axe des réels.

3.1.2. Polynôme de Chebycheff

On procède comme précédemment : \[|H(j\Omega)|^2=\frac{1}{1+\varepsilon^2~C_n^2(\Omega)}\]

\(C_n\) est le polynôme de Chebycheff d’ordre n déterminé par la récurrence suivante :

\[\begin{aligned} &C_0(x)=1\\ &C_1(x)=x\\ &C_k(x)=2~x~C_{k-1}(x)-C_{k-2}(x)\end{aligned}\]

Remarque

On démontre que les zéros Chebycheff, répartis sur une ellipse, se déduisent des zéros de Butterworth (coupure à 3 dB) répartis sur le cercle unité par une affinité géométrique.

En désignant par \(\sigma_k\) et \(\Omega_k\) les parties réelle et imaginaires des pôles, on aura respectivement :

\[\begin{aligned} &\sigma_k^2+\Omega_k^2=1 &&\text{Butterworth}\\ &\frac{{\sigma'_k}^2}{{\rm sh}(\varphi)}+\frac{{\Omega'_k}^2}{{\rm ch}(\varphi)}=1 &&\text{Chebycheff}\end{aligned}\]

Les paramètres \({\rm sh}(\varphi)\) et \({\rm ch}(\varphi)\) de l’ellipse étant déterminés par :

\[\begin{aligned} &A=\left\{\sqrt{1+\frac{1}{\varepsilon^2}+\frac{1}{\varepsilon}}\right\}^{1/N} &&B=\frac{1}{A}\\ &{\rm ch}(\varphi)=\frac{A+B}{2} &&{\rm sh}(\varphi)=\frac{A-B}{2}\end{aligned}\]

On écrit ensuite que :

\[\begin{aligned} &\sigma_k\rightarrow \sigma'_k=\Omega_k~{\rm sh}(\varphi)\\ &\Omega_k\rightarrow \Omega'_k=\sigma_k~{\rm ch}(\varphi)\end{aligned}\]

3.1.3. Polynôme de Legendre-Papoulis

On part de l’expression : \[|H(j\Omega)|^2=\frac{1}{1+\varepsilon^2~L_n(\Omega^2)}\]

\(L_n\) désigne le polynôme de Papoulis d’ordre n.

La forme de Papoulis est dite optimale : comparée à la forme de Butterworth, la courbe se maintient plate sur une grande partie de la bande passante (d’où le nom anglais de maximally flat filter) et devient assez vite abrupte en bande de transition. L’absence d’ondulations dans la bande passante garantit une qualité de phase en matière de linéarité.

Le calcul des polynômes correspondants peut paraître relativement compliqué (mais la programmation n’offre pas de grandes difficultés). Nous en donnons ici les grandes lignes.

On part des polynômes de Legendre dont la récurrence est connue :

\[\begin{aligned} P_0(x)&=1\\ P_1(x)&=x\\ n~P_n(x)&=(2~n-1)~x~P_{n-1}(x)+x^2~P_{n-2}(x)\end{aligned}\]

On engendre ensuite les polynômes de Papoulis par intégration :

Premier cas : n impair (\(n=2~k+1\))

\[L_n(\Omega^2)=\int_{-1}^{2~\Omega^2 -1}~\Big\{\sum_{i=0}^k a_i~P_i(x)\Big\}^2~dx\] \[\frac{a_i}{2~i+1}=\frac{1}{\sqrt{2~(k+1)}}\qquad (i=0,~1,~2,~\dots,~k)\]

Deuxième cas : n pair (\(n=2k+2\))

\[L_n(\Omega^2)=\int_{-1}^{2~\Omega^2 -1} (x+1)~\Big\{\sum_{i=0}^k a_i~P_i(x)\Big\}^2~dx\]

Pour ceux qui seraient intéressés par la programmation de ce type de polynômes, voici quelques résultats leur permettant de tester les algorithmes :

\[\begin{aligned} &n=2\quad~L_n(x^2)=x^4\\ &n=3\quad~L_n(x^2)=3~x^6-3~x^4+x^2\\ &n=4\quad~L_n(x^2)=6~x^8-8~x^6+3~x^4\\ &n=5\quad~L_n(x^2)=20~x^{10}-40~x^8+28~x^6-8~x^4+x^2\\ &n=6\quad~L_n(x^2)=50~x^{12}-120~x^{10}+105~x^8-40~x^6+6~x^4\\ &n=7\quad~L_n(x^2)=175~x^{14}-525~x^{12}+165~x^{10}-355~x^8+105~x^6-15~x^4+x^2\end{aligned}\]

3.1.4. Polynôme de Bessel

La fonction de transfert se présente sous une forme un peu différente des précédentes : \[H(p)=\frac{\alpha}{B_n(\lambda~p)}\]

L’expression directe du polynôme de Bessel est relativement lourde à exploiter : \[B_n(x)=\sum_{k=0}^n \frac{(2n-k)!~x^k}{2^{n-k}~k!~(n-k)!}\]

On lui préfère le polynôme généré par la récurrence suivante :

\[\begin{aligned} &B_0(x)=1\\ &B_1(x)=1+x\\ &B_k(x)=(2k-1)~B_{k-1}(x)+x^2~B_{k-2}(x)\end{aligned}\]

Le coefficient \(\alpha\) est généralement choisi pour être égal au coefficient constant de \(B_n\) de façon à garantir un affaiblissement nul (amplitude 1) à l’origine.

Le paramètre \(\lambda\) permet de contrôler le passage des courbes associées à \(B_n(p)\) au même point (\(f_p,~A_p\)).

Pour \(n\geq 3\), une bonne approximation de ce paramètre est donnée par la formule : \[A_p=\frac{10~\lambda^2}{(2n-1)~L_n(10)}\]

Remarque

Tous les polynômes de Bessel ont des zéros à parties réelle négative. Ils sont donc naturellement stables.

D’un point de vue mathématique, les filtres de Bessel présentent la meilleure linéarité en phase. En contrepartie, la raideur dans la bande de transition du gabarit est la plus faible dans la classe des filtres polynômiaux.

3.2. Approximation elliptique ou de Cauer (passe-bas)

Revenons à l’expression générale, la fonction de transfert : \[|H(p)|^2=\frac{1}{1+\varepsilon^2~|\Phi(p)|^2}\]

En approximation elliptique, la fonction caractéristique est de la forme : \[\Phi(p)=p^r\frac{\Pi_{i=1}^n(p^2+a_i^2)}{\Pi_{i=k}^m(p^2+b_k^2)}\]

Cette fonction \(\Phi\) présente la particularité d’auto-réciprocité : \[\Phi\Big(\frac{1}{x}\Big)=\frac{1}{\Phi(x)}\]

Comme un effet de levier, tous les points singuliers sont en opposition par rapport à la fréquence de normalisation (pratiquement voisine du milieu de la bande de transition) : \[f_0=\sqrt{f_p~f_a}\]

Ainsi, le dernier zéro de la bande passante sera en opposition avec la première pointe infinie de la bande atténuée. De même pour le premier zéro et la dernière pointe infinie.

Enfin, à un minimum donné de la bande passante correspondra une remontée (maximum local) dans la bande atténuée.

La détermination de cette fonction \(\Phi\) nécessite d’importants calculs. Nous donnerons ici une idée des types d’algorithmes utilisés pour déterminer la position des points critiques dont on sait qu’ils sont en auto-réciprocité par rapport à la fréquence de normalisation \(f_0=\sqrt{f_p~f_a}\).

Rappelons que la fréquence normalisée vaut : \(\Omega=\cfrac{f_p}{f_a}\)

La raideur dans la bande de transition est définie par le facteur de sélectivité : \(k=\cfrac{f_p}{f_a} \)

3.2.1. Principe général de l’algorithme

La position des points singuliers est définie au moyen des fonctions elliptiques \(sn\) de Jacobi de module \(k\) :

\[\begin{aligned} &\Omega_{0~i}=\frac{1}{\Omega_{\infty~i}}=\sqrt{k}~{\rm sn}\Big(2i~\frac{K}{N},~k\Big)\qquad i=1,~2,~...,~n\\ &\Omega_{m~i}=\frac{1}{\Omega_{M~i}}=\sqrt{k}~{\rm sn}\Big(\frac{2i-1}{N},~k\Big)\qquad i=1,~2,~...,~n\\ &N~:~\text{ordre du filtre}\\ &n=\frac{N-1}{2}\quad\text{si N impair}\quad;\quad n=\frac{N}{2}\quad\text{si N pair}\\ &K~:~\text{intégrale elliptique de première espèce de module k}\\ &K=K(k)=\int_0^{\pi/2}\frac{dx}{\sqrt{1-k^2~\sin^2(x)}}\end{aligned}\]

3.2.2. Transformations Bar et Wiggle

Si N est impair, on applique les formules précédentes.

Si N est pair, on introduit l’une des deux transformations de fréquence qui suivent :

1. Transformation Bar notée \(\overline{\Omega}\)

   Elle consiste à amener le premier zéro à l’origine. En conséquence, et par voie d’auto-réciprocité, le pôle fini le plus éloigné sera envoyé l’infini.

2. Transformation Wiggle notée \(\widetilde{\Omega}\)

   Elle impose une conservation du zéro à l’origine et une conservation du nombre de pôles. Le pôle le plus éloigné est cependant rejeté à l’infini.

3.2.3. Remarque sur la détermination de l’ordre du filtre

Le sujet de la détermination de l’ordre du filtre a été soigneusement évité. On peut effectivement l’obtenir directement par un algorithme relativement compliqué, comparé au cas des filtres polynômiaux. Cependant, il existe des réseaux d’abaques permettant d’effectuer graphiquement la recherche itérative.

Pour tous ces points particuliers et extrêmement intéressants relativement l’aspect analyse mathématique, on pourra se reporter à l’excellent ouvrage de M. Skwizynski cité en référence et qui fut ma bible.

4. Le cas des filtres large bande non passe-bas

Pour un filtre passe-bas d’origine, la normalisation de fréquence correspond à une transformation linéaire : \[p=j\omega\quad\Rightarrow\quad p_n= j\Omega=\frac{j\omega}{\omega_0}\qquad\text{où}\quad \Omega=\frac{f}{f_0}\]

Les algorithmes d’approximation nous conduisent à des coefficients de la fonction de transfert normalisée \(H(j\Omega)\). Une fois ces coefficients déterminés, il suffit de d’effectuer le remplacement \(\Omega=p/\omega_0\) pour connaître les coefficients de la fonction \(H(p)\) avec une fréquence réelle.

Des transformations non linéaires \(p_n=\mathcal{T}(p)\) permettent de convertir tout gabarit de filtre en gabarit de filtre passe-bas dit prototype passe-bas normalisé. À partir de ce gabarit intermédiaire et après calcul de la fonction de transfert correspondante, il suffit de poser \(p_n=\mathcal{T}(p)\) pour connaître les coefficients de la fonction \(H(p)\) d’origine.

Nous allons étudier succinctement deux de ces transformations, les plus répandues : la transformation passe-haut et la transformation passe-bande (la transformation coupe-bande en est une variante).

4.1. Transformation passe-haut

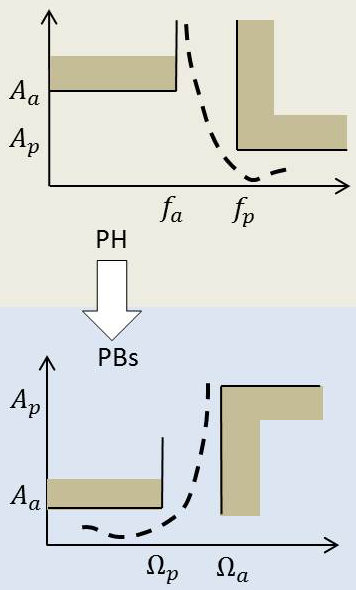En se reportant à la figure ci-contre, on notera les transformations suivantes :

\[\begin{aligned} &p=j~0\rightarrow\Omega=j~\infty\\ &p=j~\infty\rightarrow\Omega=j~0\\ &p=j~\omega_0\rightarrow\Omega=j~1\end{aligned}\]

C’est à dire : \[\Omega=\frac{\omega_0}{p}\]

La transformation n’affecte pas les affaiblissements \(A_a\) et \(A_p\).

 

4.2. Transformation passe-bande

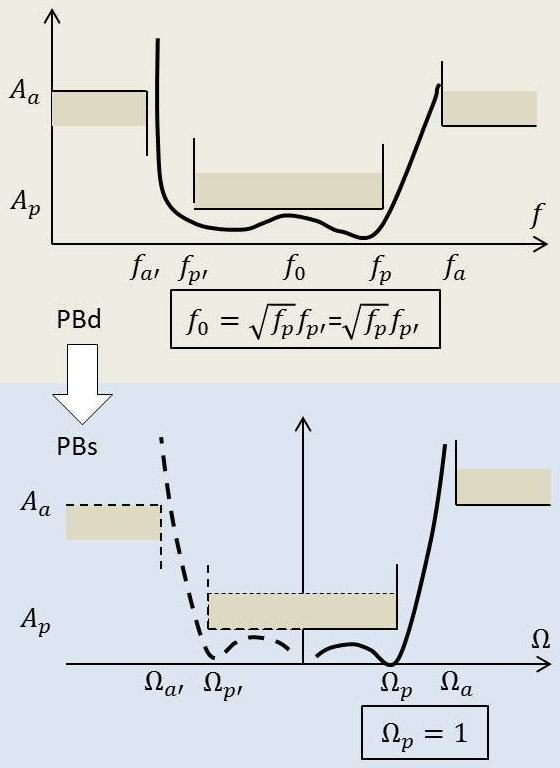Cette transformation est caractérisée par les correspondances suivantes entre les points singuliers :

\[\begin{aligned} p=j~\infty\quad&\rightarrow\quad p_n=j\Omega=j~\infty\\ p=j~0\quad&\rightarrow\quad p_n=j\Omega=j~(-\infty)\end{aligned}\]

On reconnaît les caractéristiques d’une fonction homographique : \[p_n=j~\Omega=\lambda~p+\frac{\mu}{p}\]

En étudiant les différentes correspondances et cas extrêmes, on montre que (filtres polynômiaux) :

\[\begin{aligned} \mu&=\lambda~\omega_0^2\\ \omega_0^2&=\omega_p~\omega_{p'}=\omega_a~\omega_{a'}\\ \lambda&=\frac{1}{\Delta\omega}\\ \Delta\omega&=\omega_p-\omega_{p'}\end{aligned}\]