1. Semi-conducteur de type N

Pour les applications pratiques, on utilise essentiellement les semi-conducteurs dopés, obtenus en ajoutant au matériau des impuretés bien choisies avec une concentration donnée.

Supposons que nous disposions du germanium \(Ge\) extrêmement pur (moins de 1 atome étranger pour \(10^{10}\) atomes de \(G_e\) et ajoutons lui une impureté : des atomes d’antimoine \(Sb\).

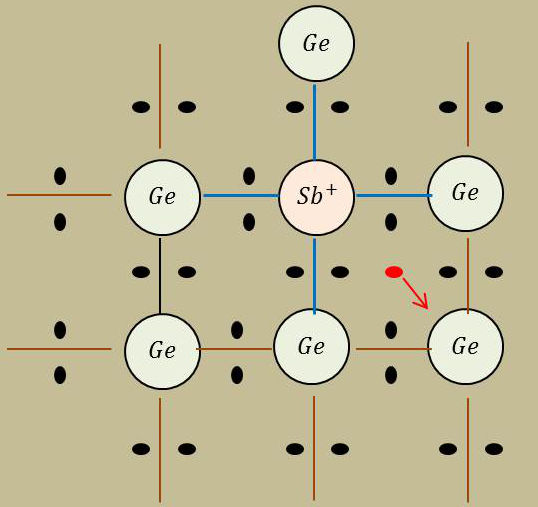Un atome \(Sb\) a un diamètre voisin de celui d’un atome \(Ge\). Il peut facilement se substituer à lui dans le réseau d’un cristal de germanium. L’antimoine \(S_b\) possède 5 électrons sur sa couche extérieure (Mendeleiev V), donc un électron de trop.

Un atome \(Sb\) remplace un atome \(Ge\), prêtant 4 électrons à ses voisins. Les 4 liaisons covalentes sont maintenues grâce à 4 autres électrons fournis par les 4 atomes \(Ge\) voisins.

L’atome \(Sb\) libère un électron qui circulera dans le réseau et devient un ion \(Sb^+\). L’atome \(Sb\) est un atome donneur.

L’ion \(Sb^+\) est fixé dans le réseau et ne contribue pas plus à la conductibilité que l’atome \(Ge\) qu’il a remplacé, mais l’électron qu’il a donné contribue à la conductibilité.

Aux faibles concentrations usuelles en impuretés (\(1\) atome \(Sb\) pour \(10^9\) à \(10^6\) atomes \(Ge\)), tous les atomes \(Sb\) sont ionisés en \(Sb^+\). Le nombre d’électrons ainsi donnés par l’antimoine dépasse de beaucoup le nombre d’électrons du germanium intrinsèque et s’ajoute pratiquement à lui.

La relation : \[n~p=n_i^2\qquad(n\gg n_i)\qquad[1]\]

est encore valable. Les électrons sont maintenant porteurs majoritaires et les trous porteurs minoritaires.

La conductibilité n’est plus : \[\sigma_i=e~n_i~(\mu_n+\mu_p)\qquad[2]\]

mais : \[\sigma=e~(n~\mu_n+p~\mu_p)~\approx~e~n~\mu_n\qquad[3]\]

Elle est considérablement augmentée, car \(n\gg n_i\). Cette augmentation étant due aux électrons (\(n\gg p\)), on a un semi-conducteur de type N.

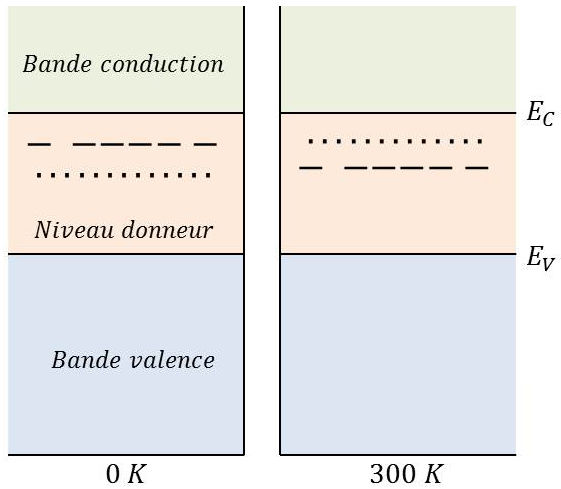Plaçons-nous dans le modèle des bandes. L’ion \(Sb^+\) du donneur se place au niveau donneur, un peu au-dessous du bas de la bande de conduction.

La position du niveau de Fermi s’obtiendrait en partant du fait que le cristal semi-conducteur est électriquement neutre : \[n=p+N_d~\approx~N_d\qquad[4]\]

(\(N_d\) concentration des ions \(S_b^+\), pratiquement la même que celle des atomes \(S_b\).

D’après la statistique de Fermi : \[\frac{n}{N_d}=1~\approx~\frac{N_c}{N_d}~\exp\Big(-\cfrac{E_c-E_F}{k~T}\Big)\qquad[5]\]

\(N_c\) : nombre des places vacantes dans la bande de conduction par unité de volume.

Ainsi, à la température ordinaire, le niveau de Fermi d’un semi-conducteur dopé N est au-dessus de celui de la même substance à l’état pur (intrinsèque). Si l’on abaisse la température, le niveau de Fermi s’élèvera jusqu’à être situé un peu au dessus du niveau donneur, mais en dessous du bas de la bande de conduction.

2. Semi-conducteur de type P

Introduisons dans du germanium pur une impureté l’indium \(I_n\) (Mendeleiev III).

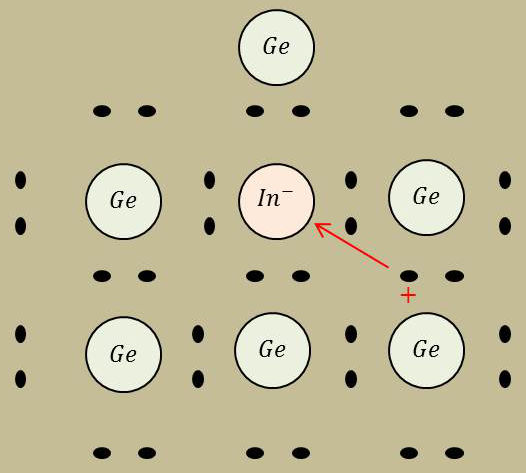L’atome d’indium n’a que 3 électrons sur sa couche extérieure. Il manque donc un électron pour constituer autour de l’atome \(I_n\) une couche de 8 électrons comme c’était le cas pour l’atome \(G_e\) auquel il s’est substitué.

L’atome \(I_n\) peut emprunter cet électron manquant à une des covalences voisines. Il devient alors un ion négatif \(I_n^-\) et il apparaît un trou positif à l’endroit où l’électron a été emprunté.

L’atome \(I_n\) qui a accepté un électron provenant d’un atome de \(G_e\) est un atome accepteur.

Les ions \(I_n^-\) sont fixés dans le réseau et ne contribuent aucunement à la conductibilité.

Soit \(N_a\) le nombre des atomes accepteurs par centimètre cube. En négligeant les trous intrinsèques éventuels en l’absence d’impureté acceptrice, \(p~\approx~N_a\). Le nombre \(n\) d’électrons est donné encore par : \[n=\frac{n_i^2}{p}=\frac{n_i^2}{N_a}\qquad[6]\]

négligeable devant \(p\). On a un semi-conducteur de type P (conduction par trous).

Chez un semi-conducteur de type P, les trous sont porteurs majoritaires et les électrons porteurs minoritaires.

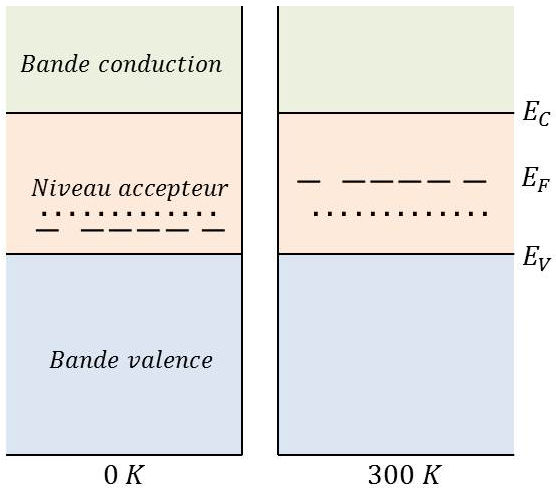Dans la théorie des bandes, les ions accepteurs sont sur un niveau accepteur peu situé au dessus de la bande de valence.

Le niveau de Fermi se trouverait d’une manière analogue à la précédente par : \[\frac{p}{N_a}=1~\approx~\frac{N_v}{N_d}~\exp\Big(-\cfrac{E_p-E_v}{k~T}\Big)\qquad[7]\]

À la température ordinaire, il est situé au dessous de celui d’un semi-conducteur intrinsèque. En agissant sur la température, il descend jusqu’à être placé un peu en dessous du niveau accepteur mais au-dessus du haut de la bande de valence.

Avec un taux d’impureté élevé, le niveau de Fermi se trouve dans la bande de conduction (atomes d’impureté donneur) ou de valence (atomes accepteurs). Le semi-conducteur est dit dégénéré, avec une conductibilité comparable à celle d’un métal.

3. Conductibilité électrique. Variation avec la température

Supposons que nous mesurions la conductibilité d’un cristal de type N en élevant progressivement sa température à partir du zéro absolu. On distingue trois domaines de variation.

3.1. Domaine 1

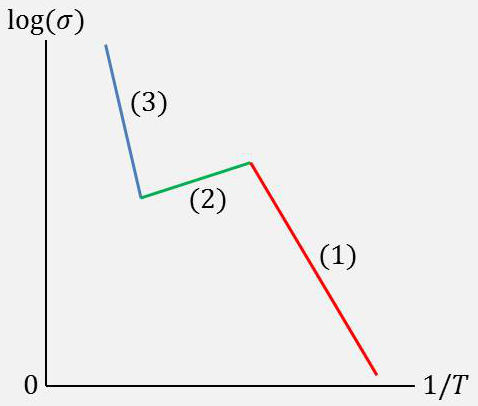À partir de 0 K, les électrons des atomes donneurs vont gagner progressivement assez d’énergie cinétique quand la température s’élève pour passer du niveau donneur jusqu’à la bande de conduction. C’est la conductibilité à basse température due au impuretés : \[\sigma=n~\mu_n\]

Elle croît avec \(T\), car le nombre d’électrons \(n\) dans la bande de conduction croît, grâce aux atomes donneurs.

3.2. Domaine 2

Lorsque tous les atomes donneurs ont fourni leur électron à la bande de conduction, leurs possibilités sont épuisées. Le nombre d’électrons de cette bande reste pratiquement constant, l’énergie thermique (\(E_{th}=k~T/2\)) étant insuffisante pour permettre un saut d’électrons à partir de la bande de valence.

La conductibilité ne reste cependant pas constante, car, dans la relation : \[\sigma=n~\mu_n\]

\(n=N_d\) reste bien constant, mais \(\mu_n\) diminue (souvent comme \(T^{-3/2}\)). C’est la conductibilité extrinsèque. La région (2) est appelée région de saturation.

3.3. Domaine 3

Si la température est suffisamment élevée, les électrons possèdent une énergie cinétique thermique suffisante pour passer de la bande de valence à la bande de conduction.

On retrouve la conductibilité intrinsèque (comme en absence de donneurs) : \[\sigma=n~\mu_n+p~\mu_p=n_i~(\mu_n+\mu_p)\]

Le même raisonnement est transposable à un semi-conducteur de type P.

4. Défauts de réseau

Les impuretés apportent donc une irrégularité au réseau cristallin : la substitution d’un ions \(S_b^+\) ou \(I_n^-\) à la place d’un atome \(G_e\).

Il existe encore plusieurs sortes de défauts qui modifient les mobilités et abrègent les durées de vie des porteurs minoritaires.

4.1. Principaux défauts

Défaut de Frenkel

Si un atome A du réseau est déplacé de sa position normale en un nœud, il se produit deux défauts simultanés :

• une lacune au nœud (où manque A) ;

• un atome interstitiel à un endroit, autre qu’un nœud (où se trouve A).

Défaut de Schottky

Si l’atome A disparaît du réseau, par exemple en diffusant vers l’extérieur du cristal, il se produit une lacune au nœud d’où A est parti.

Dislocation

Cas d’un plan réticulaire en surnombre : dislocation en arête.

Des plans réticulaires avec une autre direction que les autres : dislocation en vis.

4.2. Commentaires

Les défauts de Schottky ou de Frenkel augmentent la conductibilité ionique aux températures élevées, les lacunes facilitant le passage des électrons. Les dislocations, brisant des covalences, créent des pièges (trous ou électrons supplémentaires) qui peuvent capturer les porteurs minoritaires et en réduisent la vie moyenne.

5. Mobilités

Dans un semi-conducteur, dopé ou non, la conductibilité \(\sigma\) dépend des mobilités \(\mu_n\) et \(\mu_p\) des porteurs de charge : \[\sigma=e~(n~\mu_n+p~\mu_p)\]

L’exploitation de deux phénomènes physiques différents a permis de mesurer séparément la mobilité des porteurs de charge majoritaires et celles des porteurs minoritaires.

5.1. Premier phénomène

Supposons un échantillon semi-conducteur de type P sous forme de barreau.

De la mesure de la résistance, on déduit \(\sigma\), puis \(p\) de celle de l’effet Hall : \(p~\mu_p~\approx~\cfrac{\sigma}{e}\).

5.2. Deuxième phénomène

La mesure de la mobilité des porteurs de charge minoritaires (ici \(\mu_n\), mobilité des électrons) peut s’effectuer selon plusieurs méthodes dont celle qui suit.

Dans un barreau du semi-conducteur P, on injecte soit par un éclair lumineux, soit par une électrode auxiliaire, des électrons pendant un temps très court. On a établi au préalable un champ électrique constant \(E\) et on mesure le temps \(t\) mis par le paquet d’électrons injecté pour se déplacer d’une distance \(d\) dans le barreau.

Mesure par impulsions à l’oscillographe cathodique : \[\mu_n=\frac{(d/t)}{E}=\frac{v}{E}\]

6. Durée de vie des porteurs minoritaires

Considérons un semi-conducteur de type N : concentration \(n\) d’électrons et \(p\) de trous. Donnons à cette concentration \(p\) un accroissement \(\Delta p_0\).

Cette valeur initiale va diminuer rapidement par recombinaison de trous en excès avec des électrons jusqu’à ce que l’équilibre soit rétabli.

À un instant donné \(t\), on n’a plus qu’un excès \(\Delta p\) qui décroît exponentiellement : \[\Delta p=\Delta p_0~\exp\Big(-\frac{t}{\tau_p}\Big)\qquad[8]\]

\(\tau_p\) : durée de vie des porteurs minoritaires (ici des trous). En général, \(\tau_p\) est très petit, de l’ordre de la microseconde voire \(10^{-8}\) s. On définirait de même une durée de vie \(\tau_n\) dans un semi-conducteur de type P.

La mesure de la durée de vie des porteurs minoritaires s’effectue par plusieurs méthodes :

• Une méthode consiste à mesurer, en fonction de la distance dans le barreau, l’affaiblissement de l’impulsion recueillie dans une mesure de mobilité par injection de porteurs minoritaires.

• Une autre méthode consiste à moduler la résistance d’un barreau par un flux lumineux dont l’intensité varie en forme de créneaux rectangulaires. La résistance est diminuée par injections de porteurs minoritaires sous l’action de la lumière. Elle reprend sa valeur d’obscurité avec une constante de temps qui donne \(\tau\).

Remarques

Le barreau doit être assez long (plusieurs millimètres) pour que les recombinaisons électrons-trous en surface n’apportent pas d’erreur trop grande. Tous les défauts de réseau, en particulier les impuretés, réduisent la durée de vie des porteurs minoritaires.

7. Appendice : effet Hall, théorie simplifiée

L’effet Hall est un phénomène qui permet de connaître le signe des porteurs de charge, donc d’identifier un semi-conducteur : type N ou type P. Combiné à des mesures de conductibilité, il permet de mesurer la concentration de porteurs et leur mobilité.

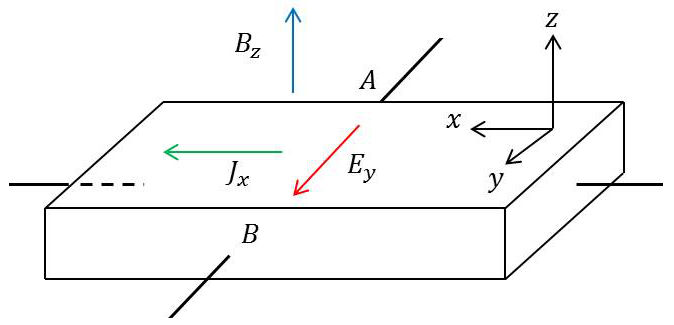Dans un parallélépipède très allongé et très mince, conducteur, un champ électrique \(\overrightarrow{E}\) produit un courant de densité \(\overrightarrow{J}\).

La conductibilité \(\sigma\) telle que \(J=\sigma\overrightarrow{E}\) est : \[\sigma=N~e~\mu\qquad[a]\]

\(e\) : charge \(\qquad\qquad\mu\)  :  mobilité

\(N\) : nombre / cm³ de porteurs de charge (supposés provisoirement d’un seul type)

Les lignes de courant sont parallèles à la longueur du parallélépipède et les équipotentielles leur sont normales.

Introduisons un champ d’induction magnétique \(\overrightarrow{B}\) perpendiculaire au plan de la bande. Les porteurs de charge sont soumis à une force qui incurve les lignes de courant. \[e~(\overrightarrow{E}+\overrightarrow{v}\wedge\overrightarrow{B})\qquad[b]\]

Des charges s’accumulent sur les parois normales à \(Oy\) jusqu’à ce que le champ électrique qu’elles créent compense l’action déviatrice du champ \(\overrightarrow{B}\).

Cet équilibre est atteint quand (champ de Hall) : \[E_y=v_x~B_z\qquad\text{avec~:}\quad J_x=N~e~v_x\qquad[c]\]

En éliminant \(v_x\) : \[E_y=J_x~\frac{B_x}{N_e}\qquad[d]\]

Si \(J\) ou \(B\) varient, \(R=\cfrac{E_y}{J_x~B_z}\qquad[e]\quad\) doit rester constant, constante que l’on appelle constante de Hall.

Cette théorie prévoit que : \[R=\frac{1}{N_e}\qquad[f]\]

Le signe de \(R\) indique le signe de la charge \(e\) : négatif (électrons) et positif (trous).

Sa mesure donne la concentration \(N\) des porteurs de charge.

En comparant les relations (a) et (b), on obtient pour la la mobilité \(\mu\) : \[\mu=R~\sigma\qquad[g]\]

donc grâce à une mesure du coefficient de Hall et une mesure de conductibilité : \[R=\frac{V~d}{I~B}\qquad[h]\]

Remarque

L’angle \(\theta\) (de l’ordre de quelques degrés) entre les surfaces équipotentielles et \(Ox\) sous l’action de \(B\) est appelé angle de Hall.

On montre que : \[\tan\theta=\frac{e~\tau}{m^*~B}\qquad[i]\]

\(\tau\) : temps moyen séparant deux collisions d’un porteur de charge avec le réseau

\(m^*\) : masse effective d’un porteur