1. Exercice 1

1.1. Enoncé

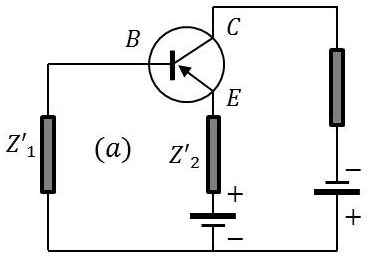On considère un transistor dans un montage en émetteur commun (cf.figure ci-contre (a)).

On cherche à établir les conditions d’oscillation de ce transistor. À cet effet :

• passer au circuit équivalent correspondant (résistances de base, d’émetteur et de collecteur auxquelles s’ajoutent les impédances externes) ;

• établir les équations des courants dans les différentes mailles du circuit ;

• étudier les solutions du système d’équations obtenues.

1.2. Réponse

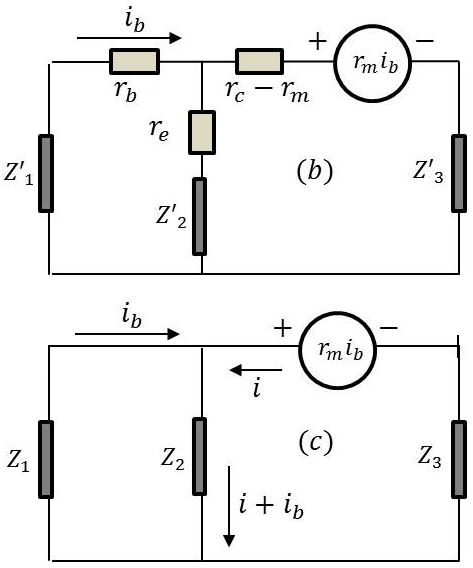On adjoint aux trois impédances extérieures le schéma équivalent en montage émetteur commun (fig. b).

On regroupe ensuite les impédances pour obtenir :

$$\begin{aligned} Z_1&=r_b+Z'_1\\ Z_2&=r_e+Z'_2\\ Z_3&=(r_c-r_m)+Z'_3\end{aligned}$$

On écrit ensuite le système des équations des mailles : $$\left\{ \begin{aligned} &i_b~(Z_1+Z_2)+i~Z_2=0\\ &i_b~(Z_2-r_m)+i~(Z_2+Z_3) \end{aligned} \right.$$

Pour qu’il y ait une solution non nulle pour les courants, le déterminant des coefficients doit être nul : $$(Z_1+Z_2)~(Z_2+Z_3)-Z_2~(Z_2-r_m)=0$$

C’est-à-dire que la condition limite d’entretien des oscillations se traduit par : $$Z_1~Z_2+Z_2~Z_3+Z_3~Z_1+Z_2~r_m=0$$

2. Exercice 2

2.1. Énoncé

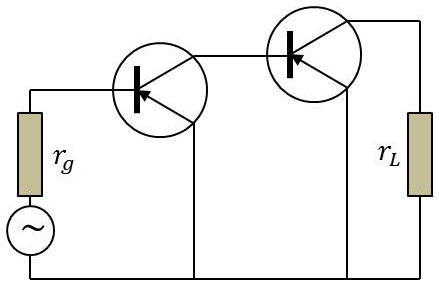On monte en cascade deux transistors à liaison directe (émetteur commun)

Calculer les gains en tension, de courant, et de puissance, sachant que :

$$\begin{aligned} r_g&=900~\Omega &&r_e=r_b=100~\Omega\\ r_c&=500~\rm k\Omega &&r_m=475~\rm k\Omega\\ r_L&=10~\rm k\Omega\end{aligned}$$

Même question si $r_g=0$.

Indication : $r_e$ et $r_b$ étant très petits, on en tiendra compte pour la simplification des calculs.

2.2. Réponse

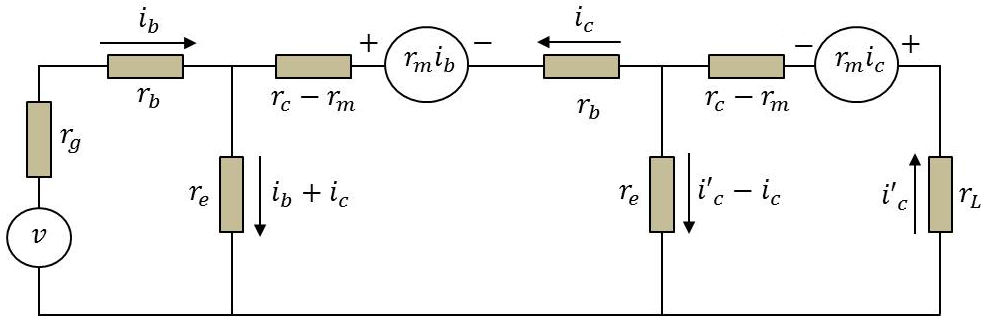On commence par établir le montage équivalent aux deux transistors montés en cascade.

On écrit comme d’habitude les équations des mailles.

Ce qui donne les relations suivantes pour les trois mailles :

$$\begin{aligned} v&=r'~i_b+r_e~i_c\qquad\text{où :}\quad r'=r_g+r_b+r_e\\ 0&=(r_e-r_m)~i_b+(r_c-r_m+2~r_e+r_b)~i_c-r_e~i'_c\\ 0&=(r_m-r_e)~i_c+(r_c-r_m+r_L+r_e)~i'_c\end{aligned}$$

Avec les simplifications autorisées, on obtient:

1. Pour le gain en courant : $$A_i~=\frac{i'_c}{i_b}\approx\frac{r_m^2}{(r_c-r_m)~(r_c-r_m+r_L)+r_e~r_m}$$

2. Pour le gain en tension : $$A_v~=~\frac{-r_L~i'_c}{r'~(r_c-r_m)^2+r_L~(r_c-r_m)^2+r_e~r_m~(r'+r_c-r_m+r_L)}$$

3. Pour le gain en puissance : $$A_p=A_i~A_v$$

Numériquement, sachant que $r'=1100~\Omega$ : $$A_i=250\quad;\quad A_v=870\quad;\quad A_p=2,18\times 10^5~~(53,4~\rm dB)$$

L’hypothèse où $r_g=0$ conduit à $r'=200$ : $$A_i~\text{inchangé}\quad;\quad A_v=1260\quad;\quad A_p=3,14\times10^5~~(55~\rm dB)$$

3. Exercice 3

3.1. Énoncé

Dans tout le problème, il s’agira d’un transistor en émetteur commun.

Les paramètres du $T$ équivalent ont, en basse fréquence, les valeurs suivantes : $$r_e=22~\Omega\quad;\quad r_b=1000~\Omega\quad;\quad r_c=2,10\times 10^6~\Omega\quad;\quad r_m=2,07\times 10^7~\Omega$$

1) Calculer, en fonction des paramètres précédents, l’expression des paramètres hybrides $h_{ij}$ et en donner les valeurs numériques.

Indiquer le schéma équivalent à deux sources utilisant ces paramètres hybrides.

2) Calculer, en fonction des paramètres hybrides $h_{ij}$ et de la résistance d’utilisation $R_u$, les expressions des caractéristiques suivantes :

• $A_i$ : gain en courant

• $A_v$ : gain en tension

• $r_i$ : résistance d’entrée

On posera : $\quad\Delta h=h_{11}~h_{22}-h_{12}~h_{21}$

3.2. Réponse

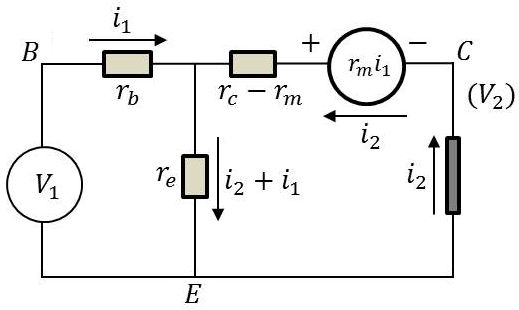1) On a ici (équations des mailles) :

$$\begin{aligned} V_1&=(r_e+r_b)~i_1+r_e~i_2 &&(1)\\ V_2&=(r_e-r_m)~i_1+(r_c-r_m+r_e)~i_2 &&(2)\end{aligned}$$

Les paramètres hybrides sont définis par la matrice $H$ :

$$\begin{aligned} V_1&=h_{11}~i_1+h_{12}~V_2 &&(3)\\ i_1&=h_{21}~i_1+h_{22}~V_2 &&(4)\end{aligned}$$

(1) s’écrit, compte tenu de (2) : $$V_1=i_1~(r_b+\frac{r_e~r_c}{r_c-r_m+r_e})+\frac{r_e}{r_c-r_m+r_e}~V_2\qquad(5)$$

(2) s’écrit : $$i_2=\frac{r_m-r_e}{r_c-r_m+r_e}~i_1+\frac{1}{r_c-r_m+r_e}~V_2\qquad(6)$$

En identifiant (5) avec (3) et (6) avec (4), on obtient les paramètres $h$ :

$$\begin{aligned} h_{11}&=r_b+\frac{r_e~r_c}{r_c-r_m+r_e} &&h_{12}=\frac{r_e}{r_c-r_m+r_e}\\ h_{21}&=\frac{r_m-r_e}{r_c-r_m+r_e} &&h_{22}=\frac{1}{r_c-r_m+r_e}\\ \Delta h&=\frac{r_b+r_e}{r_c-r_m+r_e}\end{aligned}$$

Application numérique :

$$\begin{aligned} h_{11}&\approx 1640~\Omega &&h_{12}\approx 7,33\times 10^{-4}\\ h_{21}&\approx 69 &&h_{22}\approx 3,33\times 10^{-5}~\Omega^{-1}\\ \Delta h&\approx 3,4\times 10^{-2}\end{aligned}$$

2) Calcul des caractéristiques (gains et résistance d’entrée)

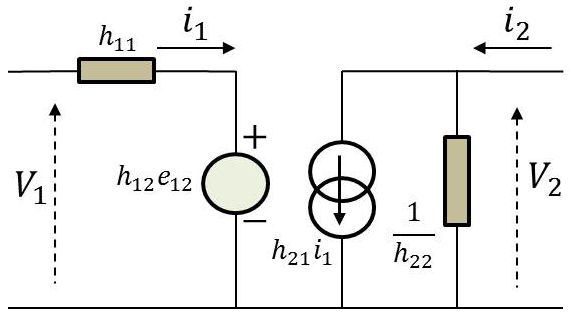On associe aux équations (3) et (4) la relation : $$V_2=-R_u~i_2$$

Ce qui permet de calculer :

$$\begin{aligned} A_i&=\frac{i_2}{i_1}=\frac{h_{21}}{1+h_{22}~R_u}\\ A_v&=\frac{V_2}{V_1}=\frac{-h_{21}~R_u}{h_{11}+R_u~\Delta h}\\ r&=\frac{V_1}{i_1}=\frac{h_{11}-R_u~\Delta h}{1+h_{22}~R_u}\end{aligned}$$

4. Exercice 4

4.1. Énoncé

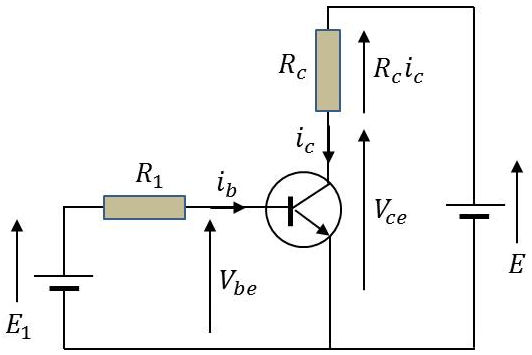On considère le montage de la figure ci-contre avec les valeurs suivantes : $$E=E_1=+20~\rm V$$

Ce transistor au silicium NPN est tel que $V_{be}$= 0,6 V en fonctionnement normal.

1) Le transistor est tel que $\beta=100$.

Calculer les valeurs à attribuer à $R_1$ et $R_c$ pour obtenir le point de repos suivant : $$I_c=20~{\rm mA}\quad\text{et}\quad V_{ce}=5~\rm V$$

2) Le transistor est tel que : $30<\beta<150$.

Déterminer à partir de quelle valeur de $\beta$ ce transistor est saturé, $R_1$ et $R_c$ ayant les valeurs précédentes.

Déterminer alors la plage de variation du point de repos du transistor, dans le réseau des caractéristiques de sortie.

4.2. Réponse

1) Calcul de $R_1$ : $$R_1=\frac{E-V_{be}}{I_c}=0,75~\rm k\Omega$$

Calcul de $R_c$ :

Tout d’abord le calcul de $i_b$ : $$i_b=\frac{i_c}{\beta}=0,2~\rm mA$$

Et ensuite : $$R_1=\frac{E-V_{be}}{i_b}=97~\rm k\Omega$$

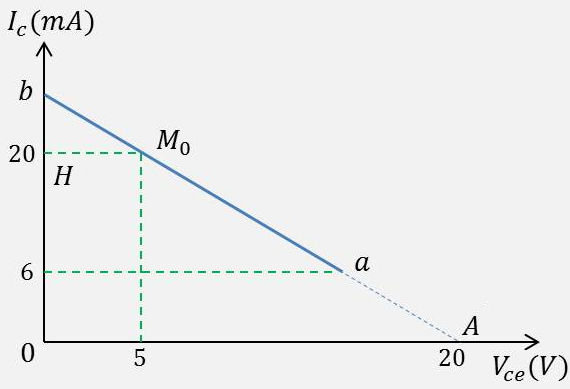2) Nous connaissons deux points de la droite de charge statique :

$$\begin{aligned} M_0~&:\quad I_c=20~{\rm mA} &&V_{ce}=5~\rm V\\ A~&:\quad V_{ce}=20~{\rm V} &&I_c=0\end{aligned}$$

Le tracé de cette droite permet de trouver $I_{c.sat}\approx$ 27 mA (point b), ceci en supposant $V_{ce.sat}\approx 0$ : $$I_{c.sat}=\frac{E-V_{ce.sat}}{R_c}\approx\frac{20~\rm mA}{0,75}$$

Soit encore $I_{c.sat}$ = 26,7 mA.

Le transistor est saturé lorsque $\beta I_b>I_{c.sat}$, soit : $$\beta>\frac{I_{c.sat}}{I_b}\quad\Rightarrow\quad\beta~>~134$$

La plage de repos est [$a,~b$].