1. Densité de probabilité et changement de variable

1.1. Énoncé

On considère un signal aléatoire \(x(t)\). La valeur de ce signal, à chaque instant \(t\), est donc une variable aléatoire \(X\).

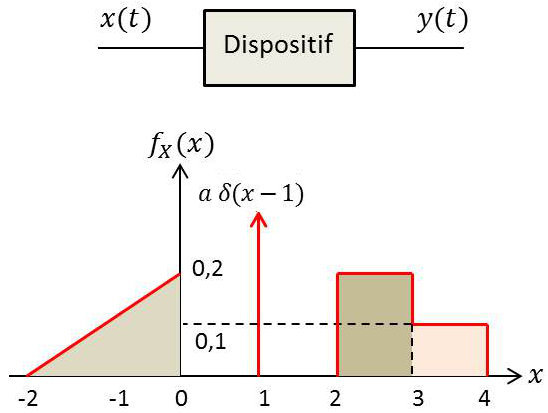
La densité de probabilité de cette variable, notée \(f_X(x)\), est représentée ci-contre (figure 2).

1) Normaliser cette densité en déterminant quelle doit être la valeur de la constante \(a\), hauteur de la composante impulsion en \(x=1\), pour que \(f_X(x)\) représente effectivement une densité de probabilité.

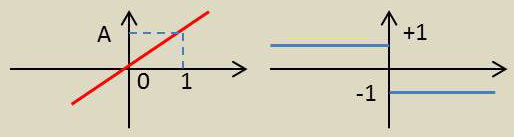2) Cette densité est maintenant appliquée à un dispositif pouvant être linéaire ou non linéaire.

Que devient l’expression de cette densité en sortie du dispositif dans les deux cas suivants ?

a) Dispositif amplificateur (\(A>0\)) ;

b) Dispositif limiteur dur (échelon Heaviside).

(On utilisera avec profit la technique du changement de variable au moyen de la fonction de répartition)

1.2. Solution

1) On exprime la condition de normalisation : \[\int_{-\infty}^{+\infty}f_X(x)~dx=1\]

Dans le cas présent, la somme suivante : \[S_1+\int a~\delta(x-1)~dx+S_2+S_3=1\]

Donc tous calculs faits : \[\Big(\frac{2\times 0,2}{2}\Big)+a+(0,2)+(0,1)=1\qquad\text{donc :}\quad a=0,5\]

2) Il y a changement de variable. On utilise donc les propriétés de la fonction de répartition : \[y=A~x\quad\Rightarrow\quad \text{Pr}(Y<y)=\text{Pr}(Ax<y)=\text{Pr}(X<\frac{y}{A})\]

a) Dispositif amplificateur

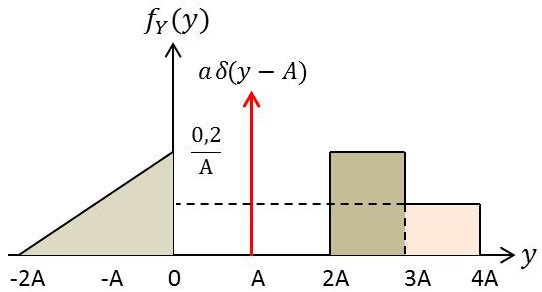La densité de probabilité étant la dérivée de la fonction de répartition, on a donc : \[f_Y(y)=\frac{1}{A}~f_X\Big(\frac{y}{A}\Big)\]

D’où la représentation figure ci-contre.

On remarquera que (propriété de distribution) : \[\frac{a}{A}~\delta\Big(\frac{y-A}{A}\Big)=a~\delta(y-A)\]

b) Dispositif limiteur dur

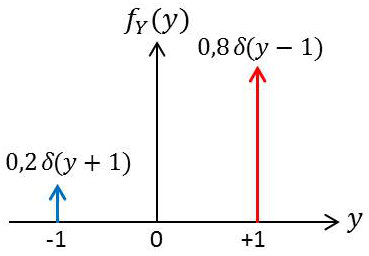
Y ne peut prendre que deux valeurs : \(Y\in\{-1,+1\}\) avec les probabilités respectives :

\[\begin{aligned} \text{Pr}[Y=-1]&=\text{Pr}[X<0]=S_1=\frac{0,2\times 2}{2}=0,2\\ \text{Pr}[Y=+1]&=\text{Pr}[X>0]=a+S_2+S_3=0,5+0,2+0,1=0,8\end{aligned}\]

On constate (fort heureusement) que la somme des deux probabilités a pour valeur 1.

La densité de probabilité en \(y\) aura alors pour expression : \[f_Y(y)=0,2~\delta(y+1)+0,8~\delta(y-1)\]

2. Fiabilité d’un système

2.1. Énoncé

Deux régulateurs contrôlent le fonctionnement d’un moteur. On veut que le moteur fonctionne sans panne pendant un temps t. La panne du moteur peut survenir avec une probabilité :

• \(q\) lorsque les deux régulateurs fonctionnent

• \(q_1\) lorsque le premier régulateur fonctionne et que le deuxième est en panne

• \(q_2\) lorsque le deuxième régulateur fonctionne et que le premier est en panne

• \(q_0\) lorsque les deux régulateurs sont en panne

La fiabilité probabilité de bon fonctionnement du premier régulateur est égale à \(P_1\) et celle du second à \(P_2\). Les éléments se mettant en panne indépendamment les uns des autres, trouver la fiabilité totale du système.

2.2. Solution

Évènement A : l’appareil fonctionne sans panne

Hypothèses :

• \(H\) les deux régulateurs fonctionnent

• \(H_1 R_1\) fonctionne et \(R_2\) est en panne

• \(H_2 R_2\) fonctionne et \(R_1\) est en panne

• \(H_0 R_1\) et \(R_2\) sont en panne

Rappelons la formule de Bayes : \[p(A)=\Sigma p(H_i)p(A/H_i)\]

Calcul des probabilités à priori :

\[\begin{aligned} p(H) &= P_1 P_2 \\ p(H_1) &= P_1 (1-P_2) \\ p(H_2) &= P_2 (1-P_1)\\ p(H_0) &= (1-P_1)(1-P_2)\end{aligned}\]

Probabilités conditionnelles de l’événement A :

\[\begin{aligned} p(A/H) &= 1-q \\ p(A/H_1) &= 1-q_1 \\ p(A/H_2) &= 1-q_2 \\ p(A/H_0) &= 1-q_0\end{aligned}\]

Par suite : \[p(A)=P_1P_2(1-q) + P_1(1-P_2)(1-q_1) + P_2(1-P_1)(1-q_2) + (1-P_1)(1-P_2)(1-q_0)\]

3. Probabilités d’appels téléphoniques

3.1. Énoncé

Un modèle simple d’appels téléphoniques est régi par la loi de Poisson. Le nombre d’appels téléphoniques durant le temps \(t\) est une variable aléatoire de paramètre \(\lambda t\) telle que : \[p(X=k) = {\lambda~t}^k~\frac{e^{-\lambda t}}{k!}\]

Le nombre moyen \(\lambda\) de communications reçues entre 10 et 11 heures est de 1,8 par minute.

Calculer la probabilité pour qu’entre 10 h 53 et 10 h 54 donc 21 minute d’observation), il y ait 0 appel, 1 appel, 2 appels, au moins 2 appels, au plus 2 appels.

3.2. Solution

On fait \(t=1\) dans la formule de Poisson :

\[\begin{aligned} P(X=0) &= e^{-1,8} = 0,16529 \\ P(X=1) &= 0,29752 \\ P(X=2) &= 0,26776 \\ P(X\geqslant 2) &= 1 - P(X=0)-P(X=1) = 0,53719 \\ P(X\leqslant 2) &= P(X=0) + P(X=1) + P(X=2) = 0,27123\end{aligned}\]

4. Fiabilité d’un système d’information

4.1. Énoncé

Une source d’information binaire E émet une suite de digits indépendants avec une probabilité \(p(1)=0,7\) et \(p(0)=0,3\). Ces informations sont transmises vers un récepteur R simultanément à travers deux canaux de transmission distincts. Ceux-ci sont perturbés de sorte qu’une probabilité d’erreur apparaît sur les deux canaux :

• \(P = 1\times 10^{-7}\) sur le premier

• \(P = 2\times10^{-7}\) sur le deuxième

À un certain instant, le récepteur reçoit de la liaison 1 un 0, et de la liaison 2 un 1. Quel est, des bits 0 et 1, celui qui a le plus de chance d’avoir été émis ?

4.2. Solution

On peut faire deux hypothèses :

• \(H_0\) : Un 0 a été émis.

• \(H_1\) : Un 1 a été émis sur le deuxième.

Une de ces hypothèses étant faite, l’évènement \(A\) (réception du couple {0, 1}) se produit. Le problème qui se pose est de savoir quelle est la plus grande des deux probabilités :

• \(H_0/A\) \(H_0\) est vérifiée alors que \(A\) s’est produit.

• \(H_1/A\) \(H_1\) est vérifiée alors que \(A\) s’est produit.

On applique la formule de Bayes :

\[\begin{aligned} p(H_0/A) &= \frac{X_0}{X_0 + X_1}\\ X_0 &= p(H_0)~p(A/H_0)\\ X_1 &= p(H_1)~p(A/H_1)\\ p(H_0) &= 0,3\quad;\quad p(H_1)=0,7\end{aligned}\]

Il reste à évaluer \(p(A/H_0)\) et \(p(A/H_1)\).

Probabilité d’une erreur sur la liaison 2 et pas d’erreur sur la liaison 1 : \[p(A/H_1)~=~2\times 10^{-7}~(1-10^{-7}~)~=~2\times 10^{-7}\]

Probabilité d’une erreur sur la liaison 2 et pas d’erreur sur la liaison 1 : \[p(A/H_0)~=~10^{-7}~(1-2\times 10^{-7})~=~10^{-7}\]

Tous calculs faits : \(p(H_0/A)~=~0,46\)  et  \(p(H_1/A)~=~0,54\)

Conclusion : C’est le symbole 1 qui a été plus probablement émis et si on décide de choisir ce symbole 1, ce sera avec une probabilité d’erreur de 0,46.

5. Probabilité de détection d’un signal bipolaire

5.1. Énoncé

Un émetteur envoie un signal bipolaire synchrone \(V\) sur un canal de transmission. À la réception, un seuil (fixé à 0 V) permet de décider si \(+V\) ou \(-V\) a été émis.

Le canal de transmission n’est pas parfait : un signal parasite \(U\) peut s’ajouter au signal utile et fausser la détection. Par exemple, si \(+V\) a été émis et si \(U<V\), alors \(V\) reçu est négatif et on décide \(-V\).

On dira que le récepteur fait une erreur quand \(+V\) est interprété alors que \(-V\) a été émis, et vice-versa.

On suppose que \(U\) est une variable aléatoire gaussienne de densité : \[f(u)=\frac{1}{\sigma~\sqrt{2\pi}}~e^{\frac{-u^2}{2\sigma^2}}\]

1) Donner l’expression de la probabilité \(P\) d’erreur dans le cas où les symboles \((0,1)\) sont équiprobables à l’émission.

2) Même question lorsque les symboles ne sont plus équiprobables. On posera :

• \(Prob(+V_{em})=P\)

• \(Prob(-V_{em})=1-P\)

avec:

• \(V_{em}\) : le signal réellement émis

• \(V_{int}\) : le signal qui sera interprété à la réception

On désignera par \(\alpha\) le nouveau seuil de décision Pour quelle valeur de \(\alpha\) la probabilité d’erreur à la détection est-elle minimale ?

5.2. Solution

1) Expression de la probabilité \(P\) :

\[\begin{aligned} P &= Prob(+V_{em}~/~-V_{int})~+~Prob(-V_{em}~/~+V_{int})\\ P &= Prob(+V_{em})\times Prob(-V_{int}~/-V_{em})+P = Prob(+V_{em})\times Prob(+V_{int}~/-V_{em})\end{aligned}\]

Dans l’hypothèse où les symboles sont équiprobables :

\[\begin{aligned} P &= \frac{1}{2} ~ Prob(U<-V)+\frac{1}{2} ~ Prob(U>V)\\ P &= \frac{1}{2} ~ \Big\{\int_{-\infty}^{-V}f(x)~dx + \int_{+V}^{+\infty}f(x)~dx \Big\}\end{aligned}\]

Et du fait de la parité de la fonction exprimant la densité gaussienne : \[P=\frac{1}{\sigma~\sqrt{2\pi}}~\int_{+V}^{+\infty}e^{\frac{-x^2}{2\sigma^2}}~dx\]

2) On écrit cette fois : \[P=p\times Prob(u<\alpha - V)+(1-p)\times Prob(u>\alpha + V)\]

On obtient ainsi : \[P = p\int_{-\infty}^{\alpha -V} f(x)~dx +~(1-p)\int_{\alpha + V}^{+\infty} f(x)~dx\]

On écrit ensuite que  \(\dfrac{dP(\alpha)}{d\alpha}=0\).

En effectuant une dérivation sous le signe \(\int\) : \[\frac{dP}{d\alpha} = \frac{1}{\sigma~\sqrt{2\pi}}~\Big\{ p~e^{-\frac{-(\alpha-V)^2}{2\sigma^2}} - (1-p)~e^{-\frac{-(\alpha-V)^2}{2\sigma^2}} \Big\} = 0\]

Tous calculs faits, on obtient: \[\alpha = \frac{\sigma^2}{2~V}~\ln\Big(\frac{1-P}{P}\Big)\]

Relation qui vérifie que pour \(P=\dfrac{1}{2}\), on a bien \(\alpha = 0\).

6. Utilisation des tables de Gauss

6.1. Énoncé

1) On suppose que la température \(T\) pendant un mois donné suit une loi normale de Gauss de moyenne \(m~=~20~^\circ\rm C\) et d’écart type \(\sigma~=~1~^\circ\rm C\). Calculer la probabilité pour que la température soit comprise entre \(21~^\circ\rm C\) et \(26~^\circ\rm C\)

2) Un échantillon de population gaussienne de moyenne \(m = 90\) et d’écart type \(\sigma = 15\) a un effectif de \(N = 150\) personnes. On veut connaître le nombre de personnes au-dessus du groupe de 110 personnes.

6.2. Solution

Courbe et table de Gauss

La partie utile de la courbe est la moitié droite, plus exactement la partie A. La flèche double (longueur \(2~\sigma\)) matérialise l’intervalle de confiance et caractérise l’acuité de la courbe.

Les probabilités indiquées dans la table correspondent à la partie droite de la courbe : \[F(t) = \frac{1}{\sqrt{2\pi}}~\int_0^t~e^{-t^2/2}~dt\]

1) Après normalisation \((t-m)~/~\sigma\)

On obtient : \(t_1 = 0,33\) ;\(i_2 = 2\)

Lecture des tables : \(p_{21}~=~0,4772\quad;\quad p_{26}~=~0,1293\)

La probabilité recherchée est donc : \[\rm prob (21~^\circ C~<~\textit{T}~<~26~^\circ C) = 0,4772 - 0,1293 = 0,3475\]

2) Écart entre les personnes :   \(\Delta N = 110 - 90 = 20\)

Il lui correspond un écart réduit :   \(\Delta N~/~\sigma = 20~/~15 = 1,33\)

Table de Gauss : à cette valeur correspond une probabilité \(p = 0,4082\), donc 42,82 % des valeurs sont comprises entre 90 et 110.

Le pourcentage au-dessus sera :   \(50 - 40,82 = 9,18\)

Le nombre de personnes correspondant sera :   \(n = 150 \times 0,0918 = 14\)