1. Diffraction

1.1. Exercice 1

1.1.1. Énoncé

On observe une source \(S\) monochromatique rectiligne (\(\lambda\) = 546 nm), placée à 10 mètres de l’observateur au travers d’une fente \(F\) (diaphragme) disposée tout contre l’œil.

Fente et source sont verticales. La position de la source coïncide avec le zéro d’une règle horizontale graduée centrée sur \(S\).

L’œil voit apparaître sur la règle les franges de diffraction de la fente.

1. Les deux premières franges d’intensité nulle bordant le maximum central coïncident avec les divisions \(\pm\) 27 cm de la règle. Quelle est la largeur de la fente ?

2. La distance de ces franges est lue à \(\pm 1\text{cm}\) près et la mesure supposée faite à 20 % près.

   Quelle est la largeur maximale de la fente mesurable avec cette précision ?

3. Quelle est la largeur maximale de la fente donnant des franges visibles (c’est-à-dire séparables par l’œil), la limite de résolution angulaire de l’œil étant de l’ordre de 3,10\(^{-4}\) rad ?

1.1.2. Solution

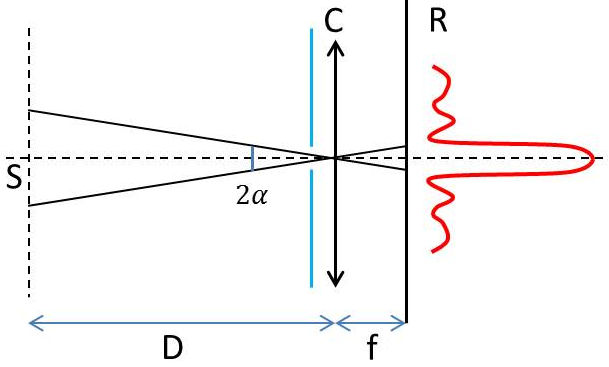1) L’œil constitue un système optique dont la lentille est le cristallin \(C\) et le plan d’observation la rétine \(R\).

Lorsque l’œil accommode sur \(S\),on obtient en \(R\), alors plan conjugué de la source, le diagramme de diffraction.

Rappelons (voir le cours), que les deux premiers maximums secondaires encadrant le maximum central ont pour abscisses (\(a\) étant la largeur de la source) : \[X=\pm\frac{f}{a}\]

Leur distance angulaire est (hypothèse des petits angles) : \[2\alpha\approx\frac{2~X}{f}=\frac{2~\lambda}{a}\]

L’œil accommodant sur \(S\) observe une coïncidence de ces deux maxima secondaires avec deux divisions de la règle distantes de : \[d=2~\alpha~D\]

On en déduit la largeur de la fente : \[a=\frac{2~\lambda}{2~\alpha}=\frac{2~\lambda~D}{d}\]

Application numérique : \(a~\approx~2\times 10^{-2}~\text{mm}\)

2) Pour que la largeur maximale de la fente soit mesurable à 20 % près, il faut que : \[\frac{\Delta a}{a}=\frac{\Delta d}{d}~\leq~0,2\]

Comme on suppose que \(\Delta d=1~\text{cm}\), on doit avoir \(d\geq 5~\rm cm\).

On obtient alors : \[a=\frac{2~\lambda~D}{d}=0,22~\text{mm}\]

3) La distance angulaire de deux franges noires consécutives doit être supérieure à la limite de résolution de l’œil : \[\frac{\lambda}{a}\geq 3\times 10^{-4}\qquad\text{soit :}\quad a\leq 1,8~\text{mm}\]

2. Interférences

2.1. Exercice 1

2.1.1. Énoncé

Deux fentes de Young sont distantes de 0,2 mm. L’écran d’observation est distant de 1 m.

1. La 3\(^{me}\) frange brillante est située à 7,5 mm de la frange centrale. Calculer la longueur d’onde de la lumière utilisée.

2. Même question en supposant que c’est la 3\(^{me}\) frange sombre qui est à 7,5 mm de la frange centrale.

2.1.2. Solution

1) Rappelons la formule de l’interfrange : \[i=\frac{\lambda~D}{a}\]

\(\qquad a=0,2~{\rm mm}\quad;\quad D=10^3~{\rm mm}\quad;\quad i=7,5/3=2,5~\rm mm\)

On a donc : \[\lambda=\frac{a~i}{D}=0,5\times 10^{-3}~\rm mm=0,5~\mu m\]

2) La distance à la frange centrale de la 3\(^{me}\) frange sombre étant de 2,5 interfranges, on a : \[i'=\frac{7,5}{2,5}=3~\rm mm\]

On a donc : \[\lambda'=\frac{a~i'}{D}=0,6\times10^{-3}\rm ~mm=0,6~\mu m\]

2.2. Exercice 2

2.2.1. Énoncé

Interférences à trois sources.

On considère un dispositif interférentiel constitué par un diaphragme (\(D\)) percé de trois fentes \(F_1,~F_2,~F_3\) très fines, équidistantes (\(F_1F_2=F_2F_3=d\)) et normales au plan de la figure.

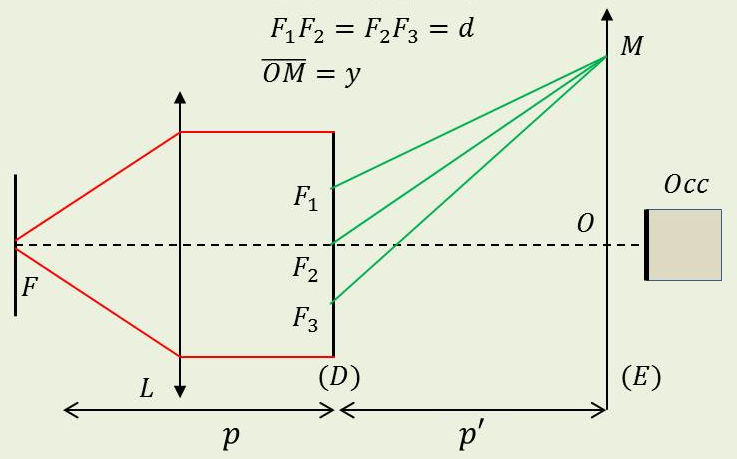Le système est éclairé en lumière monochromatique de longueur d’onde \(\lambda\) par une fente source très fine, parallèle aux trois fentes, et disposées au foyer objet d’une lentille \(L\).

On observe à travers un oculaire les phénomènes d’interférences obtenus dans un plan (\(E\)) situé à la distance \(p'\) des trois fentes.

On désignera par \(p\) la distance \(FF_2\) et par \(\varphi\) la différence de phases, en un point \(M\) du plan \((E)\), entre les vibrations diffractées par deux fentes consécutives \(F_1,~F_2\) ou \(F_2,~F_3\).

On donne :\(\quad d=0,5~{\rm mm}\quad;\quad \lambda=546~{\rm nm}\quad;\quad p'=50~\rm cm\).

1. On ferme la fente \(F_2\). Décrire brièvement le phénomène observé dans la plan (\(E\)). Calculer et représenter graphiquement, en fonction de \(\varphi\), la valeur de l’intensité lumineuse en \(M\). Donner la valeur numérique de l’interfrange.

2. On ouvre la fente \(F_2\) de manière à lui donner la même largeur (très faible) qu’aux fentes \(F_1\) et \(F_3\). Calculer la valeur de l’intensité en \(M\), les positions des maximums et des minimums, l’interfrange.

2.2.2. Solution

1) Origine des phases : phase en M de la vibration \(s_2\) diffractée par \(F_2\).

Déphasages pour \(F_1\) (en avance) et \(F_2\) (en retard) : \[\varphi=2\pi~\frac{\delta}{\lambda}\]

Avec : \[\delta=F_1F_2~\sin\theta\approx\theta~d\approx\frac{y~d}{p'}\]

Problème classique des fentes de Young.

L’élongation résultante en \(M\) est : \[s=s_1+s_2=a~\{\cos(\omega~t+\varphi)+\cos(\omega~t-\varphi)\}=2~a~\cos\varphi~\cos\omega~t\]

Et l’intensité : \[I=4~a^2~\cos^2\varphi\]

Maximum : \(\varphi=k~\pi\)

Minimum : \(\varphi=\cfrac{\pi}{2}+k~\pi\)

Interfrange : \(i_1=\cfrac{\lambda~p'}{2~d}\)

2) Fentes \(F_1,F_2,F_3\) identiques

En \(M\) interfèrent trois vibrations : \[s_1=a\cos(\omega~t+\varphi)\quad;\quad s_=a~\cos~\omega~t\quad;\quad s_3=a~\cos(\omega~t-\varphi)\]

Élongation résultante : \[s=s_1+s_2+s_3=a~(1+2~\cos\varphi)~\cos~\omega~t\]

Intensité résultante : \[I=a^2~(1+2\cos\varphi)^2\]

Minimum : \[I=0\quad\Rightarrow\quad\cos\varphi=-\frac{1}{2}\quad;\quad\varphi=\frac{2\pi}{3}+2~k~\pi\]

Maximums principaux : \[I=9~a^2\quad\Rightarrow\quad\varphi=2~k~\pi\]

Maximums secondaires : \[I=a^2\quad\Rightarrow\quad\varphi=\pi+2~k~\pi\]

Même interfrange que précédemment, mais les maximums successifs ne sont plus égaux.