1. Radioactivité 1
1.1. Énoncé
On a observé sur 1 gramme de chlorure de rubidium environ 480 désintégrations par seconde. Cette radioactivité est due à l’isotope \(^{87}\)Rb, émetteur \(\beta\) dont l’abondance relative \(R\) dans le rubidium naturel est voisin de 28 %.
On demande de calculer, à partir de ces données, la période du radio-élément.
Masses molaires : \(m_{\rm Rb}\) = 85,5 g mol\(^{-1}\) ; \(m_{\rm Cl}\) = 35,5 g mol\(^{-1}\).
1.2. Solution
Masse d’une mole de RbCl : \[M~=~85,5~+~35,5~=~121~\rm g\]
Il contient (nombre d’Avogadro) : \[\mathcal N~=~6,02\times 10^{23}~\text{molécules}\]
Nombre de noyaux de Rb contenus dans 1 g de RbCl : \[\frac{\mathcal N}{M}\]
Nombre de noyaux de \(^{87}\)Rb : \[N~=~\frac{\mathcal N}{M}~\times~R\]
Activité de ce rubidium : \[A~=~\lambda~N~=~480~\text{Bq (désintégrations par seconde)}\]
On a donc : \[\lambda~=~\frac{480}{N}~=~\frac{480\times 121}{6,02\times 10^{23}\times 0,28}~=~3,44\times 10^{-19}~\rm s^{-1}\]
Pour la période ou demi-vie, on sait que :
\[\begin{aligned} T~&=~\frac{\ln 2}{\lambda}~=~\frac{0,693}{3,44\times 10^{-19}}~=~2,0\times 10^{18}~\rm s \\ \text{soit :}\quad T~&=~6,3\times 10^{10}~\text{ans}~=~63\text{ milliards d'années}\end{aligned}\]
2. Radioactivité 2
2.1. Énoncé
1) On enferme dans une ampoule 0,1 cm³ de radon \(^{222}\)Rn dans les conditions normales de température et de pression. Le gaz est monoatomique.
La période de l’élément est \(T\) = 3,52 jours.
Quelle est l’activité en becquerels ?
2) La série des désintégrations est la suivante : \[\rm ^{222}Rn~~\xrightarrow{\alpha}{}~~RaA~~\xrightarrow{\alpha}{}~~RaB~\xrightarrow{\beta}{}~RaC~~\xrightarrow{\beta}{}~~RaC'~~\xrightarrow{\alpha}{}~~RaD~~\xrightarrow{\beta}{}~~RaD~~\xrightarrow{\beta}{}\]
Les périodes des corps A, B, C, C’ sont inférieures à la demi-heure.
La période du RaD est \(T\) = 22 ans.
Quelle est la masse de RaD que l’on obtiendra au bout de 2 mois ?
Quelle sera l’activité de l’ampoule au bout de ce délai ?
2.2. Solution
Rappelons que le volume correspondant à une mole gazeuse est : \[V_0~=~22,4~\rm L~=~22~400~cm^3\]
Le volume de radon considéré (0,1 cm³) correspond à un nombre de noyaux est égal à : \[N~=~\frac{\mathcal{N}\times~0,1}{22~400}~=~\frac{(6,022\times 10^{23})\times~0,1}{22~400}~=~2,69\times10^{18}\]
1) Valeur de la constante radioactive (1 j = 86 400 s) : \[\lambda~=~\frac{\ln 2}{T}~=~\frac{0,693}{3,52\times 86~400}\rm ~s^{-1}\]
\[\frac{0,693~\times~(2,69~\times~10^{18})}{3,82~\times 86~400}~=~5,65\times 10^{12}~\rm Bq~=~5650~GBq\]
2) Une durée de 2 mois correspond à 60 / 3,52 = 17 périodes.
La quantité de radon sera donc divisée par \(2^{17}\approx 130~000\).
Vu les très faibles périodes de RaA, RaB, RaC et RaC’, pratiquement, tout le radon se sera transformé en RaD et une très faible proportion seulement de RaD s’est désintégrée puisque la période est égale à 22 ans.
L’activité du RaD sera donc (1 an = \(3,16\times 10^7\) s) : \[\frac{0,693~\times~(2,69~\times~10^{18})}{22\times 3,16\times 10^7}~=~2,35\times 10^{9}~\rm Bq~=~2,35~GBq\]
L’activité du radon restant : \[\frac{5,65\times 10^{12}}{130~000}~=~4,35\times 10^7~\rm Bq~=~0,0435~GBq\]
Celles de RaA, RaB, RaC et RaC’ seront identiques, les désintégrations correspondantes étant très rapides.
L’activité globale de l’ampoule sera celle de la somme des activités de ses constituants : \[(2,35\times 10^{9})+5\times(4,35\times 10^7)~=~2,57\times 10^9~\rm Bq~=~2,57~GBq\]
3. Radioactivité 3
3.1. Énoncé
On a 1 gramme de radium (Ra) pur et notamment entièrement privé de radon (Rn).
Calculer la masse de radon formée au bout de 1 heure, 4 jours, 8 jours à partir des activités correspondantes en becquerels.
Établir à cette occasion une formule générale reliant l’activité d’une certaine quantité de corps à sa masse.
Période du radium = 1602 ans ; période du radon = 3,82 jours
3.2. Solution
Par définition, l’activité de 1 gramme de radium est égale à 1 curie, unité historique de radioactivité qui vaut \(3,7\times 10^{10}\) Bq.
Étant donnée la très grande période du radium, cette quantité peut être considérée comme constante pendant toute la durée de l’expérience.
Affectons l’indice 1 au radium et l’indice 2 au radon.
Dans un intervalle de temps \(dt\), il se détruit :
\[\begin{aligned} dN_1~&=~-\lambda_1~N_1~dt \quad\text{noyaux de radium}\\ \text{et}\quad dN_2~&=~-\lambda_2~N_2~dt \quad\text{noyaux de radon}\end{aligned}\]
Variation du nombre d’atomes de radon pendant \(dt\) :
\[\begin{aligned} dN_2~&=~\lambda_1~N_1~dt~-~\lambda_2~N_2~dt\\ \frac{dN_2}{dt}~+~\lambda_2~N_2~~&=~\lambda_1~N_1\end{aligned}\]
On sait que la résolution de cette équation donne (voir le cours V, § 3.1) : \[\lambda_2~N_2~=~\lambda_1~N_1~\{1-\exp(-\lambda_2~t)\}\]
Avec : \[T_2~=~3,82~{\rm j}\qquad;\qquad\lambda_2~=~\frac{\ln 2}{T_2}~=~\frac{0,693}{3,82 \times 86~400}~=~2,10 \times 10^{-6}~\rm s^{-1}\]
Tous calculs faits : \[\begin{matrix} &t&\exp(-\lambda_2~t)&A_2\\ &1~\rm h &0,9925&0,0075~\rm Ci = 0,28~GBq\\ &4~\rm j &0,485&0,515~\rm Ci = 19,1~GBq\\ &8~\rm j &0,235&0,765~\rm Ci = 28,3~GBq \end{matrix}\]
Calcul des masses
Nombre d’atomes de radium (\(i=1\)) et de radon (\(i=2\)) : \[N_i~=~\frac{m_i}{M_i}~\mathcal{N}\qquad;\qquad N_2~=~\frac{m_2}{M_2}~\mathcal{N}\]
Pour les masses : \[m_2~=~\frac{N_2~M_2}{N_1~M_1}~m_1~=~\Big\{\frac{\lambda_2~N_2}{\lambda_1~N_1}~\frac{T_2}{T_1}~\frac{A_2}{A_1}\Big\}~m_1\]
Or, à partir de la définition de l’activité :
\[\begin{aligned} A_i~&=~\lambda_i~N_i~=~\frac{\ln(2)}{T_i}~N_i \\ N_i~&=~\frac{T_i~A_i}{\ln(2)}\end{aligned}\]
Donc : \[m_2~=~\frac{M_2~A_2~T_2}{M_1~A_1~T_1}~m_1\]
On sait que :
\[\begin{aligned} 1~{\rm g~Ra}~~\rightarrow~~A_1&=1~\rm Ci=3,7 \times 10^{10}~Bq\\ M_1&=226~{\rm g~mol^{-1}}\quad;\quad T_1=1,602 \times 10^3~\text{ans}\quad;\quad m_1=1~{\rm g}\\ {\rm Rn}~~\rightarrow~~M_2&=222~{\rm g~mol^{-1}}\quad;\quad T_2=\frac{3,82}{365}=1,046 \times 10^{-2}~\rm an\end{aligned}\]
Tous calculs faits, en grammes :
\[\begin{aligned} m_2~&=~6,65 \times 10^{-6} \times A_2 \qquad (A_2 \text{ en curies}) \\ \text{ou}\quad m_2~&=~1,80 \times 10^{-16} \times A_2 \qquad (A_2 \text{ en béquerels})\end{aligned}\]
En se référant aux chiffres du premier tableau, on obtient numériquement : \[\begin{matrix} &t& & &m_2\\ &\rm 1~h& & &4,99\times 10^{-8}~\rm g\\ &\rm 4~j& & &3,42\times 10^{-6}~\rm g\\ &\rm 8~j& & &5,09\times 10^{-6}~\rm g \end{matrix}\]
4. Rayonnement – absorption
4.1. Énoncé
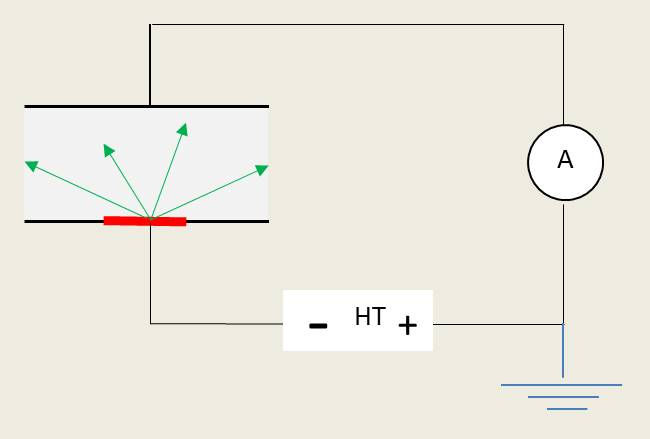On considère une source mince de polonium 210, de 1 microcurie placée entre les armatures d’un condensateur, comme indiqué sur la figure.
Le dispositif permet de collecter tous les ions produit par chaque \(\alpha\).
On rappelle que l’émission des \(\alpha\) est isotrope.
Quel est le courant que l’on mesure dans le circuit de l’appareil A (électromètre ou microampèremètre) ?
On admettra que l’apparition d’une paire d’ions induit dans le circuit une charge égale à la charge élémentaire.
1 curie : \(\rm 1~Ci~=~3,7\times 10^{10}~Bq\) (1 béquerel = 1 désintégration par seconde)
Énergie des \(\alpha\) du polonium 210 : 5,3 MeV
Énergie nécessaire pour produire une paire d’ions dans l’air : 35 eV
Charge élémentaire : \(e~=~1,6\times 10^{-19}~\rm C\) (coulomb)
4.2. Solution
La source émet : \[N~=~3,7\times 10^{10} \times 10^{-6}~=~3,7 \times 10^4~\rm particules~\alpha\]
Du fait de l’isotropie, une moitié seulement se répand dans le gaz de la chambre : \[\frac{N}{2}~=~1,85 \times 10^4~\rm particules~\alpha\]
Chaque particule produit : \[n~=~\frac{5,3 \times 10^6}{35}~=~1,515\times 10^5~\text{paires d'ions}\]
Le courant cherché est égal à : \[I~=\frac{N}{2}~n~e\]
Ce qui donne : \[I~=~1,85\times 10^4 \times 1,515 \times 10^5 \times 1,6 \times 10^{-19}~=~4,48 \times 10^{-10}~\rm A\quad\text{(ampère)}\]
5. Réactions nucléaires 1
5.1. Énoncé
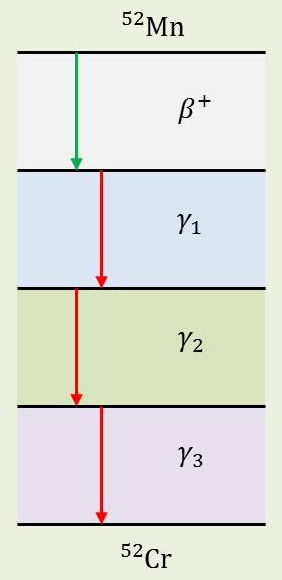Une partie du schéma de désintégration du manganèse 52 est représentée dans la figure ci-contre.
Les énergies de réaction sont les suivantes : \[\begin{matrix} &\beta^+& &0,58~\rm MeV\\ &\gamma_1^+& &0,73~\rm MeV\\ &\gamma_2^+& &0,94~\rm MeV\\ &\gamma_3^+& &1,46~\rm MeV \end{matrix}\]
1) Calculer la masse atomique du manganèse 52.
2) Calculer le seuil de la réaction nucléaire \(\rm ^{52}Cr(p,n)~^{52}Mn\), ???????? c’est-à-dire l’énergie minimum des protons.
On donne les valeur des masses atomiques :
\[\begin{aligned} M(\rm ^{52}Cr)~&=~51,9571~\rm g~mol^{-1} \\ M(\rm proton)~&=~1,00813~\rm g~mol^{-1} \\ M(\rm neutron)~&=~1,00896~\rm g~mol^{-1}\end{aligned}\]
5.2. Solution
1) La désintégration de\(~^{52}\)Mn qui conduit au\(~^{52}\)Cr est une désintégration \(\beta^+\).
Le bilan de cette désintégration et l’état fondamental du\(~^{52}\)Cr est donc : \[E_1~=~\{M(^{52}{\rm Mn})-M(^{52}{\rm Cr})-2~m_e\}~c^2\]
\(M\) : masse atomique \(\quad;\quad m_e\) : masse de l’électron
Dans une désintégration par électron (positif ou négatif) ou lors d’une émission \(\gamma\) nucléaire l’énergie de recul du noyau résiduel est négligeable.
On peut donc écrire : \[E_1~=~\widehat{E}_c(\beta^+)~+~E(\gamma_1)~+~E(\gamma_2)~+~E(\gamma_3)\]
\(\widehat{E}_c(\beta^+)\) : énergie maxima du \(\beta^+\)
C’est-à-dire numériquement : \[E_1~=~0,58~+~0,73~+~0,94~+~1,46~=~3,71~\rm MeV\]
On tient compte de plus de l’énergie relative aux deux électrons : \[2~m_e~c^2~=~1,02~\rm MeV\]
On rappelle par ailleurs la valeur de l’énergie équivalente à une unité de masse atomique : \[u~c^2~=~(1,66054 \times 10^{-27}~\rm kg)\times(2,99792 \times 10^8~m/s)^2~=~4,978Ê \times 10^{-21}~J~=~931~MeV\]
On obtient donc : \[M(^{52}{\rm Mn})~=~M(^{52}{\rm Cr})~+~\frac{3,71+1,02}{931}~=~51,9622~\rm MeV\]
2) Considérons la réaction : \[p~+~^{52}{\rm Cr}\quad\rightarrow\quad n~+~^{52}\rm Mn\]
Le bilan de cette réaction est égal à :
\[\begin{aligned} &E_2~=~\{~M({\rm p})~+~M(^{52}{\rm Cr})~-~M({\rm n})~-~M(^{52}{\rm Mn})\}~c^2\\ &E_2~=~-~\{~M(^{52}{\rm Mn})~-~M(^{52}{\rm Cr})~+~M({\rm n})~-~M({\rm p})\}~c^2\\ &E_2~=~(51,9622-51,9571+1,00896-1,00813)\times 931\\ &E_2~=~4,73-0,77~=~5,50~\rm MeV\end{aligned}\]
On sait que dans une relation nucléaire du type : \[a~+~X\quad\rightarrow\quad b~+~Y\]
dans laquelle le bilan de réaction \(E\) est négatif (réaction endoénergétique) et ne mettant pas en œuvre des énergies relativistes, l’énergie de seuil est donnée par l’expression : \[E_s~=~-E~\frac{m_b+m_Y}{m_b+m_Y-m_a}\]
On aura ici : \[E_s\approx 5,50\times \frac{53}{52}=5,61~\rm MeV\]
6. Réactions nucléaires 2
6.1. Énoncé
La capture d’un neutron lent par un noyau de bore 10 conduit à la réaction : \[\rm ~^{10}B~+~n\quad\rightarrow\quad^7Li~+~\alpha\]
Dans le cas où le noyau de lithium est produit dans son état fondamental, calculer, en MeV, l’énergie libérée par la réaction et les énergies cinétiques de la particule \(\alpha\) et du noyau de lithium.
On donne les valeurs des masses atomiques :
\[\begin{aligned} M(\rm ^4He)~&=~4,003873~\rm g~mol^{-1} \\ M(\rm ^7Li)~&=~7,018223~\rm g~mol^{-1} \\ M(\rm ^{10}B)~&=~10,016114~\rm g~mol^{-1} \\ M(\rm ^1n)~&=~1,008982~\rm g~mol^{-1}\qquad (neutron)\end{aligned}\]
6.2. Solution
On a la réaction : \[\rm ~_0^1n~+~~_5^{10}B\quad\rightarrow\quad_2^4He~+~_3^7Li\]
Bilan de la réaction : \[E~=~\{M(^{10}{\rm B})~+~M({\rm n})~-~M(^4{\rm H})~-~M(^7{\rm Li})\}~c^2\]
Numériquement : \[E~=~(10,016114+1,008982-4,003873-7,018223) \times 931\]
Soit : \[E~=~0,00300\times 931~=~2,793~\rm MeV\]
Comme il s’agit d’une réaction par neutrons lents, le système du laboratoire et celui du centre de masse sont pratiquement confondus, de telle sorte que le bilan de réaction est disponible dans ce système sous forme d’énergie cinétique des deux produits de réaction.
De la loi de conservation des impulsions, on tire : \[|\overrightarrow{p_{(\alpha)}}|~=~|\overrightarrow{p}_{(^7\rm Li)}|\]
Ou encore : \[m_{\alpha}~E_{(\alpha)}~=~m_{(^7\rm Li)}~E_{(^7\rm Li)}\]
C’est-à-dire : \[4~E_{(\alpha)}~=~7~E_{(^7\rm Li)}\]
La conservation totale de l’énergie donne : \[E~=~E_{(\alpha)}~+~E_{(^7\rm Li)}\]
De ces deux équations, on tire :
\[\begin{aligned} E_{(\alpha)}~&=~E~\frac{m_{(^7\rm Li)}}{m(\alpha)+m_{(^7\rm Li)}}~\approx~\frac{7}{11}\times 2,793~=~1,778~\rm MeV\\ E_{(^7\rm Li)}~&=~E~\frac{m_{\alpha}}{m(\alpha)+m_{(^7\rm Li)}}~\approx~\frac{4}{11}\times 2,793~=~1,015~\rm MeV\end{aligned}\]
