1. Support d’une fonction

Le support d’une fonction à valeurs complexes définie sur \(\mathbb{R}\) est le plus petit ensemble fermé en dehors duquel cette fonction est nulle.

Citons deux exemples simples :

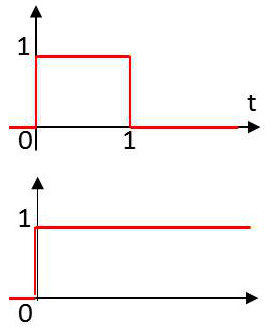
1. La fonction caractéristique \(\chi\) : \[\chi~:~\qquad\text{support}~\chi_{0,1}=[0,1]\]

2. La fonction échelon de Heaviside : \[Y~:~\qquad\text{support}~Y=[0,+\infty[\]

2. Espace \(\mathcal D\) des fonctions test \(\varphi\)

\(\mathcal D\) est l’espace des fonctions complexes définies sur \(\mathbb R\) indéfiniment dérivables à support borné. Dans ce qui suit, on ne cherchera pas à déterminer ces fonctions : celles-ci portent le nom de fonctions test et elles agissent en auxiliaires.

Leurs propriétés sont remarquables pour leur association passagère à d’autres fonctions :

1. \(\mathcal{D}\) est un espace vectoriel de dimension infinie.

2. Si \(\varphi\in\mathcal{D}\), alors sa dérivée \(\varphi'\in\mathcal{D}\).

3. Si \(\varphi\in\mathcal{D}\) et si \(\alpha~: \mathbb{R}\rightarrow\mathbb{C}\) est indéfiniment dérivable, alors \(\alpha.\varphi\in\mathcal{D}\).

En effet, \(\alpha.\varphi\) est indéfiniment dérivable et : support(\(\alpha.\varphi)\subset\) support(\(\varphi)\).

2.1. Topologie dans \(\mathcal{D}\)

Une suite \(\varphi_n\) (\(n\) > 0) de fonctions de \(\mathcal{D}\) converge vers une fonction \(\varphi\in\mathcal{D}\) quand \(n\) tend vers l’infini si :

1. Il existe un ensemble borné \(B\subset\mathbb{R}\) tel que \(\forall n\in \mathbb N\), support \((\varphi_n) \in B\).

2. Pour tout entier \(k\geq 0\), la suite des dérivées \(\varphi_n^{(k)}\) converge uniformément sur \(\mathbb{R}\) quand \(n\) tend vers l’infini vers la dérivée correspondante \(\varphi^{(k)}\).

   On notera qu’à chaque ordre k (et pas pour tous les k à la fois), il y a convergence uniforme.

3. Espace \(\mathcal{D'}\) des distributions

Une distribution \(T\) est une fonctionnelle linéaire continue sur l’espace vectoriel \(\mathcal{D}\).

À tout \(\varphi\subset\mathcal{D}\) , on associe le nombre complexe noté \(T(\varphi)\) ou en général \(\langle T,\varphi\rangle\) par les crochets de dualité :

\[\begin{aligned} &\varphi\subset\mathcal{D}~\xrightarrow{~~T~~}~\langle T,\varphi\rangle\in\mathbb{C}\\ &\forall\varphi\in\mathcal{D},~\forall\psi\in\mathcal{D},~\forall\lambda\in\mathcal{D}~:\qquad \langle T,\varphi+\lambda.\psi\rangle~=~\langle T,\varphi\rangle + \lambda\langle T,\psi\rangle\end{aligned}\]

Soit \(\varphi_{n>0}\) une suite d’éléments de \(\mathcal{D}\).

Si \(\varphi\in\mathcal{D}\) et si \(\{\varphi_n\rightarrow\varphi\}_{n\rightarrow\infty}\) , alors la suite des nombres complexes \(\langle T,\varphi_n\rangle\) converge vers le nombre \(\langle T,\varphi\rangle\) : \[\varphi_n\xrightarrow{~~D~~}\varphi\qquad\Rightarrow\qquad lim_{n\rightarrow\infty}~\big[\langle T,\varphi_n\rangle\big]=\langle T,\varphi\rangle\]

L’ensemble des distributions, noté \(\mathcal{D'}\), est un espace vectoriel :

Pour \(S\in\mathcal{D'},~T\in\mathcal{D'},~\varphi\in\mathcal{D},~\lambda\in\mathbb{C}\) :

\[\begin{aligned} \langle S+T,\varphi\rangle &= \langle S,\varphi>+<T,\varphi\rangle\\ \langle\lambda.S,\varphi\rangle &= \lambda.\langle S,\varphi\rangle\end{aligned}\]

\(\mathcal{D'}\) est donc une partie du dual algébrique de \(\mathcal{D}\).

4. Cas particuliers

4.1. Fonction localement intégrable

Soit la fonction \(f~:~\mathbb{R}\rightarrow\mathbb{C}\) : \[\forall a,b\in\mathbb{R}~;~ a<b\qquad \int\limits_a^b|f(t)|~dt<+\infty\]

On lui associe une distribution \(T_f\) : \[\langle T_f,\varphi\rangle=\int\limits_{-\infty}^{+\infty}f(t)~\varphi(t)~dt\qquad \varphi\in\mathcal{D}\]

Cette intégrale a un sens, car \(\varphi\) est nulle à l’extérieur d’un ensemble borné.

4.2. Distribution de Dirac \(\delta\)

La distribution de Dirac \(\delta\) est définie par :

\[\begin{aligned} \langle\delta,\varphi\rangle &= \varphi(0)\\ \langle\delta_{(a)},\varphi\rangle &= \varphi(a)\end{aligned}\]

Elle peut être physiquement interprétée comme une masse (ou une charge) ponctuelle de valeur unité à l’origine (notation \(\delta\)) ou plus généralement en un point d’abscisse \(a\) (notation \(\delta_a\) ou \(\delta_{(a)}\)).

4.3. Valeur principale (VP)

Pour la facilité de l’exposé, nous raisonnons sur un exemple.

La distribution valeur principale de \(\Big(\cfrac{1}{x}\Big)\), notée \(vp~\Big(\cfrac{1}{x}\Big)\), est définie par :

\[\begin{aligned} \big\langle vp\Big(\frac{1}{t}\Big),\varphi\big\rangle~&=~lim~_{\epsilon>0\rightarrow 0}~\bigg\{\int\limits_{|t|>\epsilon]}\frac{\varphi(t)}{t}~dt\bigg\}\\ &=~lim~_{\epsilon>0\rightarrow 0}~\bigg\{\int\limits_{-\infty}^{-\epsilon}\frac{\varphi(t)}{t}~dt+\int\limits_{+\epsilon}^{+\infty}\frac{\varphi(t)}{t}~dt\bigg\}\end{aligned}\]

Le calcul est ramené à la somme de deux intégrales, la valeur intermédiaire \((t=0)\) ayant été exclue.

Vérifions succinctement la légitimité de ce subterfuge en s’assurant que cette valeur principale est une distribution tempérée pour tout \(R>0\) . On peut écrire : \[\int\limits_{|t|>\epsilon]}\frac{\varphi(t)}{t}~dt~=\int\limits_{\epsilon<|t|<R}\frac{\varphi(t)-\varphi(0)}{t}~dt+\int\limits_{|t|>R}\frac{\varphi(t)}{t}~dt\]

\(\varphi\in\mathcal{D}\) étant bornée et \([\varphi(t)-\varphi(0)] / t\) ayant une limite (la dérivée), l’égalité ci-dessus prouve que l’intégrale précédente a bien une limite quand \(\epsilon\) tend vers 0.

On peut d’ailleurs écrire : \[\big\langle vp\Big(\frac{1}{t}\Big),\varphi\big\rangle~=\int\limits_{-R}^{+R}\frac{\varphi(t)-\varphi(0)}{t}~dt\]