1. Dérivation au sens des distributions
1.1. Généralités
Soit la fonction \(f~:~\mathbb{R}\rightarrow\mathbb{C}\) de classe \(\mathbb{C}^1\) (à dérivée première continue).
\[\begin{aligned} \langle T_{f'},~\varphi\rangle~&=~\int_{\mathbb{R}}f'(t)~\varphi(t)~dt\\ \langle T_{f'},~\varphi\rangle~&=~\Big[f(t)~\varphi(t)\Big]_{-\infty}^{+\infty}-\int_{\mathbb{R}}f(t)~\varphi'(t)~dt\\ \langle T_{f'},~\varphi\rangle~&=~-\langle T_{f},~\varphi'\rangle\end{aligned}\]
On écrit, de manière impropre : \[\langle T',~\varphi\rangle~=~-\langle T,~\varphi'\rangle\]
Par récurrence : \[\langle T^{(k)},~\varphi\rangle=(-1)^k~\langle T,~\varphi^{(k)}\rangle\]
Ainsi, toute distribution est indéfiniment dérivable.
1.2. Distribution de Dirac
Distribution en un point \(a\) : \[\begin{aligned} \langle \delta_a',~\varphi\rangle~&=~\langle \delta_a,~\varphi'\rangle=-\varphi'(a)\\ \langle \delta_{(a)}^{(k)},~\varphi\rangle~&=~(-1)^k~\varphi^{(k)}(a)\end{aligned}\]
Distribution à l’origine : \[\begin{aligned} \langle \delta',~\varphi\rangle ~&=~-\langle \delta,~\varphi'\rangle~=~-\varphi'(0)\\ \langle \delta^{(k)},~\varphi\rangle ~&=~-(1)^k~\varphi^{(k)}(0)\end{aligned}\]
1.3. Fonction discontinue
On s’intéresse ici à une discontinuité de première espèce.
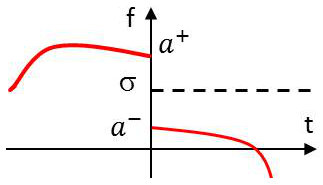
L’expression du saut de la fonction est donnée par : \[\sigma_a=f(a^+)-f(a^-)\]
On veut calculer la dérivée \((T_f)'\) de \(T_f\) : \[\begin{aligned} \big\langle (T_f)',~\varphi\big\rangle ~&=~-\langle T_f,~\varphi'\rangle \\ \big\langle (T_f)',~\varphi\big\rangle ~&=~-\int_{-R}^a f(t)~\varphi'(t)~dt-\int_a^R f'(t)~\varphi(t)~dt\end{aligned}\]
En intégrant par parties et en considérant les spécificités de la fonction test \(\varphi\) : \[\begin{aligned} \varphi(-R) &= \varphi(+R) = 0 &&\text{valeurs extêmes en dehors du support}\\ \varphi(a^+) &= \varphi(a^-) = \varphi(a) &&\text{continuité à l’intérieur du support}\end{aligned}\]
Il vient : \[\begin{aligned} \big\langle (T_f)',~\varphi\rangle ~&=~ \sigma_a~\varphi(a)+\int_{-R}^{+R}f'(t)~\varphi(t)~dt\\ \big\langle (T_f)',~\varphi\rangle ~&=~ \sigma_a~\langle \delta_a,~\varphi\rangle+\langle T_{f'},~\varphi\rangle\\ \big\langle (T_f)',~\varphi\rangle ~&=~ \langle \sigma_a~\delta_a+T_{f'},~\varphi\rangle\end{aligned}\]
On a donc : \[(T_f)'=T_{f'}+\sigma_a~\delta_a\]
Dans le cas d’une fonction continue (saut de valeur nulle) : \[(T_f)'~=~T_{f'}\]
Formule généralisable à un ensemble de sauts : \[(T_f)'~=~T_{f'}+\sum_{i=1}^{n}\sigma_{a_i}~\delta_{a_i}\]
1.4. Exemples de dérivées de fonctions
1.4.1.
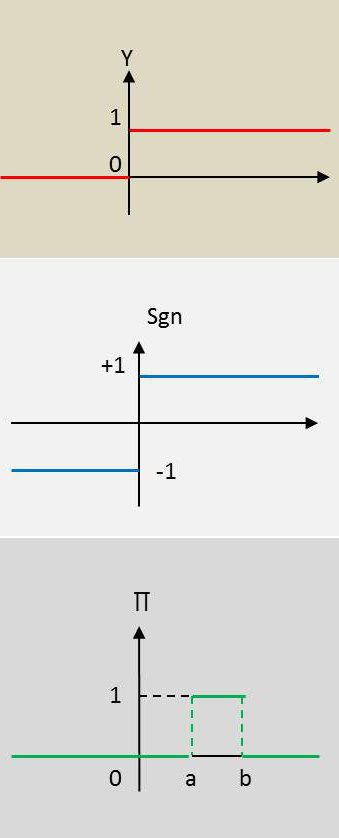
La valeur du saut en zéro est \(\sigma=0\).
La fonction a une valeur constante de part et d’autre de la discontinuité (dérivée nulle).
On a donc : \[(Y)'=\delta\]
1.4.2. Fonction Signe
La fonction Signe est définie par : \[\text{sgn}(t)=\left\{ \begin{aligned} &+1\qquad t>0\\ &-1\qquad t<0 \end{aligned} \right.\]
Le saut de la fonction a pour valeur \(\sigma=+2\).
On a donc : \[\{\text{sgn(t)}\}'=2~\delta\]
1.4.3.
Partout constante ou nulle (donc de dérivée nulle).
Elle possède deux sauts qui sont respectivement : \[\sigma_a=+1\quad;\quad \sigma_b=-1\]
On a donc : \[\{\Pi(t)\}'~=~\delta_a-\delta_b\]
2. Multiplication des distributions
Stricto senso, on ne peut pas multiplier deux distributions entre elles.
Cependant, si \(\alpha\) est une fonction indéfiniment dérivable et si \(T\in\mathcal{D'}\), alors le produit \(\alpha~T\) a un sens et \(\alpha~T\in\mathcal{D'}\).
Si \(\varphi\in\mathcal{D'}\), on posera : \[\langle \alpha~T,~\varphi\rangle~=~\langle T,~\alpha~\varphi\rangle\]
et pour une fonction qui est localement intégrable : \[\alpha~T_f=T_{\alpha f}\]
Ces propositions découlent de l’écriture intégrale dans laquelle il est possible de permuter la place des fonctions sans modifier la valeur de l’intégrale. En effet : \[\begin{aligned} \langle T_f,~\varphi\rangle &=\int_{\mathbb R} f(t)~\{\varphi(t)~dt\}\\ \langle \alpha T_f,~\varphi\rangle &= \int_{\mathbb R} f(t)~\{\alpha(t)~\varphi(t)~dt\}=\int_{\mathbb R} f(t)~\alpha(t)~\{\varphi(t)~dt\}\end{aligned}\]
2.1. Application 1
Nous allons montrer que, au sens des distributions : \[(\alpha~T)'~=~\alpha'~T+\alpha~T'\]
En utilisant la propriété : \[\big\langle(\alpha~T)',~\varphi\big\rangle~=~-\langle \alpha~T,~\varphi'\rangle ~=~-\langle T,~\alpha~\varphi'\rangle\]
nous avons : \[\begin{aligned} \langle \alpha~T'+\alpha'~T,~\varphi\rangle ~&=~\langle \alpha~T',~\varphi\rangle +\langle \alpha'~T,~\varphi\rangle ~=~\langle T',~\alpha~\varphi\rangle + \langle T,~\alpha'~\varphi\rangle \\ &=~-\langle T,~(\alpha~\varphi)'\rangle +\langle \alpha'~T,~\varphi\rangle ~=~-\langle T,~\alpha'~\varphi+\alpha~\varphi'\rangle \\ &=~-\langle T,~\alpha~\varphi'\rangle -\langle T,~\alpha'~\varphi\rangle +\langle \alpha'~T,~\varphi\rangle ~=~-\langle T,~\alpha~\varphi'\rangle ~=~ \langle (\alpha~T)',~\varphi\rangle \end{aligned}\]
2.2. Application 2
La propriété de multiplication induit un résultat remarquable avec la distribution de Dirac, résultat très utilisé dans les techniques de calcul de la théorie et du traitement de signal.
Considérons, pour simplifier l’écriture, le cas de la distribution à l’origine \(\delta(t)\).
On s’intéresse au produit \(\psi(t)~\delta(t)\) : \[\begin{aligned} \langle \delta(t)~\psi(t),~\varphi(t)\rangle ~&=~\langle \delta(t),~\psi(t)~\varphi(t)\rangle~=~\psi(0)~\varphi(0)\\ &=~\psi(0)~\langle \delta(t),~\varphi(t)\rangle~=~\langle \psi(0)~\delta(t),~\varphi(t)\rangle\end{aligned}\]
Par suite : \[\delta(t)~\psi(t)~=~\psi(0)~\delta(t)\]
Plus généralement : \[\delta_a(t)~\psi(t)~=~\psi(a)~\delta_a(t)\]
En particulier : \[\psi(t)=t\qquad\Rightarrow\qquad t~\delta(t)=0\]
En dépit de sa trivialité, cette formule est extrêmement importante, car l’élément neutre, introduit sous forme de distribution, peut garantir une homogénéité dans une relation donnée.
Nous énoncerons sans démonstration la condition nécessaire et suffisante :
Pour qu’une distribution \(T\in\mathcal{D}\) vérifie \(x~T=0\), il faut et il suffit que \(T=k~\delta\) (proportionnalité avec la distribution de Dirac).

