1. Introduction

Nous allons définir et décrire quelques formes mathématiques classiques, dites lois de probabilité, permettant de caractériser les pondérations \(p_i\) s’il s’agit de variable aléatoire discrète ou la densité \(f(x)\) s’il s’agit de variable aléatoire continue.

2. Loi de distribution uniforme

Toutes les valeurs susceptibles d’être prises par la variable aléatoire \(X\) dans l’intervalle \([a, b]\) sur lequel elle est définie sont équiprobables. Ce qui s’exprime par : \[f(x)= \begin{aligned} &\lambda \text{ constante}\quad && a \leq x < b \\ &0 && \text{ailleurs} \end{aligned}\]

\(\lambda\) est une constante à déterminer de telle sorte que la fonction soit normalisée. C’est-à-dire : \[\int_{-\infty}^{+\infty}f(x)~dx=\int_a^b\lambda~dx=1 \quad\Rightarrow\quad \lambda=\frac{1}{b-a}=\frac{1}{L}\]

La valeur \(\lambda=1/L\) correspond bien à une notion physique d’homogénéité.

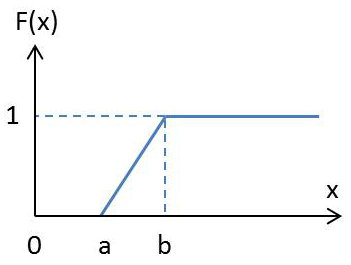Pour la fonction de répartition, on peut immédiatement obtenir les valeurs hors intervalle par continuité avec les valeurs extrêmes :

\[\begin{aligned} & x<a &&F(x)=0\\ & x>b &&F(x)=1\\ & a<x<b &&F(x)=\int_a^x\frac{dx}{b-a}=\frac{x-a}{b-a}\end{aligned}\]

Remarque : Il est intuitivement normal de retrouver une fonction linéaire dans l’intervalle d’existence.

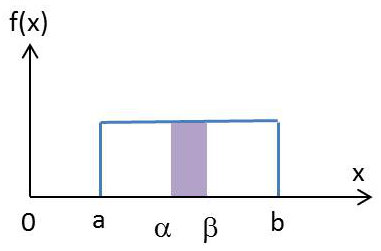D’autre part : \[Pr(\alpha<X<\beta)=F(\beta)-F(\alpha)=\frac{\beta-\alpha}{b-a}\]

On retrouve bien la notion physique de linéarité ou d’homogénéité avec le rapport des surfaces.

Pour la fonction caractéristique : \[\Phi(t)=\int_a^b\frac{1}{b-a}e^{jtx}dx=\frac{1}{b-a}\cdot\frac{e^{jtb}-e^{jta}}{jt}\]

3. Loi de Poisson

La loi de Poisson est une loi de probabilité discrète qui décrit le comportement du nombre d’évènements se produisant dans un laps de temps fixé, si ces évènements se produisent avec une fréquence moyenne connue et indépendamment du temps écoulé depuis l’évènement précédent. Cette loi est également pertinente pour décrire le nombre d’évènements dans d’autres types d’intervalles, spatiaux plutôt que temporels, comme des segments, surfaces ou volumes.

La loi de Poisson s’applique à une variable discrète. La loi de Poisson de paramètre \(a\) (qui est la valeur moyenne) est définie par son tableau de répartition : \[\begin{Bmatrix} \text{Variable :}&0&1&2&\dots&k\\ \text{Probabilité :}&e^{-a}&ae^{-a}&\frac{a^2}{2!}e^{-a}&\dots&\frac{a^k}{k!}e^{-a} \end{Bmatrix}\]

3.1. Moment d’ordre 1

\[\begin{aligned} &m_1=E(X)=\sum_{k=0}^{k=+\infty}k~\frac{a^k}{k!}~e^{-a}\\ &m_1=a~e^{-a}\sum_{k=1}^{+\infty}\frac{a^{k-1}}{(k-1)!} =a~e^{-a}\sum_{l=0}^{+\infty}\frac{a^l}{l!} \\ &m_1=a~e^{-a}.e^a=a\end{aligned}\]

3.2. Moment d’ordre 2

Calcul préliminaire :

\[\begin{aligned} E\big\{X(X-1)\big\}&=\sum_{k=0}^{+\infty}k(k-1)~\frac{a^k}{k!}~e^{-a} =a^2e^{-a}\sum_{k=2}^{+\infty}\frac{a^{k-2}}{(k-2)!} \\ E\big\{X(X-1)\big\} &=a^2~e^{-a}~e^a=a^2\end{aligned}\]

Or, on a : \[E\big\{X(X-1)\big\}=E(X^2)-E(X)=m_2-a\]

Par suite, pour la variance et l’écart type : \[\sigma^2=m_2-m_1^2=a \quad\text{et}\quad \sigma=\sqrt{a}\]

Calcul de la fonction caractéristique : \[\Phi(t)=\sum_{k=0}^{+\infty}e^{jtk}~\frac{a^k}{k!}~e^{-a}=e^{-a}\sum_{k=0}^{+\infty}\frac{(a^{jt})^k}{k!}=e^{a(e^{jt}-1)}\]

4. Loi de Gauss ou loi normale

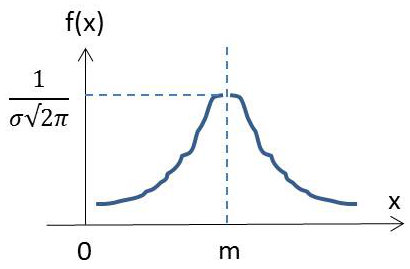La loi de Gauss a un rôle très important en théorie des probabilités. Elle a la particularité d’être une loi limite vers laquelle tendent les autres lois pour des conditions se rencontrant fréquemment dans les applications pratiques.

\(X\) est une variable continue prenant toutes les valeurs dans l’intervalle \([-\infty,+\infty]\) suivant la loi de densité : \[f(x)=\frac{1}{\sigma\sqrt{2\pi}}\cdot\exp\left(-\frac{(x-m_1)^2}{2\sigma^2}\right)\]

On peut vérifier que :

\[\begin{aligned} E(X)&=\sum_{-\infty}^{+\infty}x~f(x)~dx=m_1\\ E(X-m_1)^2&=\sum_{-\infty}^{+\infty}(x-m_1)^2~f(x)~dx=\sigma^2\end{aligned}\]

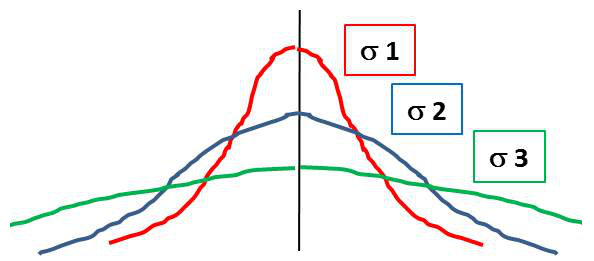Ainsi les deux paramètres \(m_1\) et \(\sigma\) définissent complètement la loi de Gauss. Le paramètre \(m_1\) caractérise la position du maximum. Le paramètre \(\sigma\) caractérise forme de la courbe : plus \(\sigma\) est grand, plus la courbe est sélective. On dit encore que \(\sigma\) est un paramètre de dispersion.

Si \(m_1=0\) et \(\sigma=1\) , la loi est dite réduite : \[f(x)=\frac{1}{\sqrt{2\pi}}~e^{-x^2/2}\]

4.1. Courbe de Gauss : interprétation

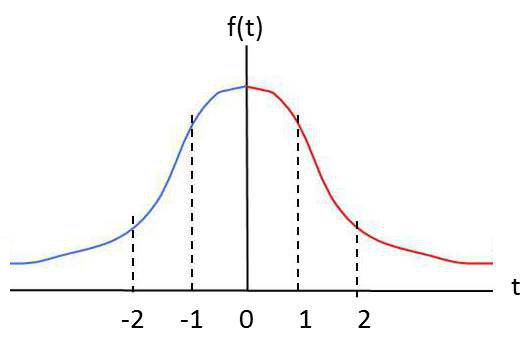La courbe ci-contre représente le graphe de : \[f(t)=\frac{1}{\sqrt{2\pi}}~e^{-t^2/2}\]

Dans le cas d’une variable réduite (\(m=0 \ ; \ \sigma=1\)), le graphe est symétrique par rapport à l’axe des ordonnées. On peut noter que la surface comprise dans l’intervalle \([-1;+1]\) correspond approximativement à 68 % de la surface totale de valeur unité. En unités réelles, cet intervalle serait \([-\sigma;+\sigma]\).

La signification physique (sens statistique) est la suivante :

Si un échantillon suit une loi de répartition gaussienne, 68 % de la population se situe dans \([m-\sigma;m+\sigma]\). L’intérêt d’un paramètre le plus petit possible est le centrage de la population vers la valeur moyenne, autrement dit, la concentration du maximum d’individus vers cette valeur.

Supposons qu’il s’agisse d’un lot de résistances de valeur moyenne \(R_0=100~\Omega\) pour lequel \(\sigma=1~\Omega\). On pourra dire que 68 % des résistances (prises au hasard) seront situées dans la gamme \([99~\Omega~;~101~\Omega]\).

En affinant le processus (\(\sigma\) de plus en plus petit), la qualité du lot est alors mieux garantie.

4.2. Table de Gauss : utilisation

Les tables normalisées de Gauss résultent de la valeur de l’intégrale : \[F(t)=\frac{1}{\sqrt{2\pi}}\int_0^t~e^{-t^2/2}~dt \qquad 0\leq t < +\infty\]

Il s’agit de la fonction de répartition et on sait que : \[F(t)=Pr(0\leq X<t)\]

Les tables donnent les valeurs de l’intégrale pour \(t\geq 0\).

On pourra remarquer que \(F(1)=0.34\) ce qui concorde avec l’estimation à \(2\times 0.34\), soit \(68~\%\).

4.3. Exercice d’application

Un échantillon de population gaussienne de moyenne \(m=800\), d’écart-type \(\sigma=400\) est constitué par \(1000\) membres. On veut connaître le nombre de personnes au-delà de \(900\).

Réponse

• Écart réel de ces personnes : \(1000-900=100\)

• Écart réduit de ces personnes : \(100\div 400=0.25\)

• Probabilité de cet écart (consultation de la table) : \(p=0.4938\)

• Pourcentage au-dessus correspondant : \(50-49.38=0.62\)

Le nombre cherché est donc : \(N = \text{Partie entière de } (0.0062\times 1000) = 6\)

5. Loi binomiale

Ayant en mémoire l’épreuve du jeu de pile ou face, on considère l’ensemble de \(n\) variable aléatoires indépendantes \({X_1,~X_2,~\dots,~X_n}\) de tableau de répartition : \[X_i= \begin{Bmatrix} &0&1&\\ &p&q& \end{Bmatrix} \qquad p+q=1\]

Elle permet de constituer une variable \(Z=\sum X_i\) telle que : \[Z= \begin{Bmatrix} &0& \dots &k& \dots &n&\\ &q& \dots &C_n^k~p^k~q^{n-k}& \dots .&p^n& \end{Bmatrix}\]

On appelle cette répartition loi binomiale.

On remarque que les coefficients pondérateurs sont les coefficients du développement du binôme \((a+b)^n\) que l’on peut connaître à n’importe quel ordre grâce au triangle de Pascal rappelé ici à titre informatif (jusqu’à l’ordre 5) : \[\begin{matrix} &1&1&\\ &1&2&1\\ &1&3&3&1\\ &1&4&6&4&1\\ &1&5&10&10&5&1 \end{matrix}\]

La variable aléatoire \(Z\) peut prendre les valeurs discrètes \(\{0,~1,~2,~\dots,~n\}\), avec les probabilités : \[Pr(X=k)~: \quad \pi_k=C_n^k~p^k~q^{n-k}\]