1. Variable aléatoire et fonction aléatoire

Il faut bien distinguer les deux notions suivantes :

• Une variable aléatoire est une grandeur qui peut, dans une expérience, prendre une valeur quelconque inconnue à l’avance. Cette valeur est appelée réalisation.

• Une fonction aléatoire est une fonction qui peut, dans une expérience, adopter une forme quelconque inconnue à l’avance. La forme prise par cette fonction lors d’une expérience est appelée réalisation.

2. Génération de processus

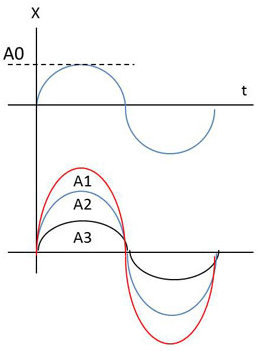
On considère la sinusoïde \(X(t)=A~\sin(\omega t)\). Quand l’amplitude \(A\) est certaine \((A=A_0 )\), on obtient une sinusoïde parfaite. Les valeurs aléatoires de \(A\) sont voisines de \(A_0\) (moyenne) ; à chacune d’entre elles correspond une sinusoïde.

\(X(t)\) est en fait une famille de courbes et la fonction \(X(t)\) en tant que telle prend un caractère aléatoire. On dit alors qu’il s’agit d’un processus aléatoire ou stochastique.

 
 

3. Loi de répartition

3.1. Notion de section

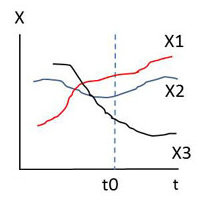
Si on fixe \(t=t_0\), alors \(X(t_0)\) devient une variable aléatoire au sens habituel du terme. On dit que c’est la section de la fonction aléatoire correspondant à \(t=t_0\) donné.

3.2. Loi de répartition

En s’attachant à une section (\(t\) fixé), on peut définir une loi de probabilité \(f(x,t)\) comme dans le cas d’une variable aléatoire. Cette définition est insuffisante, l’idéal étant de définir le processus en plusieurs points \(\{x_1,~x_2,~\dots,~x_n\}\), d’où la loi de probabilité \(f(x_1,~x_2,~\dots,~x_n~;\) \(t_1,~t_2,~\dots,~t_n)\). Ceci est naturellement impensable.

C’est pourquoi, dans l’étude des lois de répartition des fonctions aléatoires, on se limite généralement aux cas particuliers où, pour caractériser complètement une fonction aléatoire, il suffit par exemple de connaître la fonction \(f(x_1,~x_2~;~t_1,~t_2)\). C’est le processus de post-action.

4. Moments des fonctions aléatoires

On retrouve les notions définies pour les variables aléatoires, mais ce sont ici des fonctions du temps : \[\begin{aligned} m&= E(X)=\overline{X}\\ \sigma^2&=E{(X-m)}^2 \end{aligned} \qquad \Rightarrow \begin{aligned} m(t)&=E\{X(t)\}\\ \qquad \sigma^2(t)&=E\{X(t)-m(t)\}^2 \end{aligned}\]

5. Fonction d’auto-corrélation

Le coefficient d’auto-corrélation \(r\) entre deux variables aléatoires \(X\) et \(Y\) permet de se faire une idée de la dépendance stochastique entre ces deux variables. Si, au lieu de ces deux variables, on en a une infinité constituant une fonction aléatoire X(t), on obtiendra des renseignements intéressants sur la structure de cette fonction en étudiant le coefficient de corrélation entre \(X(t_1)\) et \(X(t_2)\) pour les deux valeurs quelconques de \(t\) appartenant à l’intervalle de définition. On définit ainsi ce que l’on appelle la fonction d’auto-corrélation de X(t) : \[R_{xx}(t_1,t_2)=E\{X(t_1)~X(t_2)\}\]

Elle est parfois notée \(\gamma(t_1,t_2)\).

5.1. Quelques propriétés remarquables

Symétrie \[R_{xx}(t_1,t_2)=R_{xx}(t_2,t_1)\]

Il s’ensuit que : \[R_{xx}(t_1,t_1)=E\{X(t_1)\}^2\]

Inégalité de Schwartz

Il s’agit en fait d’une conséquence de l’inégalité de Schwartz : \[{[\gamma(t_1,t_2)]}^2\leq\gamma(t_1,t_1)~\gamma(t_2,t_2)\]

5.2. Exemple

On considère la fonction : \[X(t)=A\cos(\omega t)+B\sin(\omega t)\]

• \(A\) et \(B\) sont des variables aléatoires, réduites et indépendantes.

• La variable \(\omega\) est donnée.

• \(X(t)\) est donc une fonction aléatoire.

D’après les hypothèses d’indépendance et de réduction : \[\begin{aligned} E(AB)=E(A)~E(B)=0\\ E(A^2)=E(B^2)=\sigma^2=1\end{aligned}\] Le calcul du produit \(X(t_1)X(t_2)\) est une somme de trois termes : \[\begin{aligned} &A^2\cos(\omega t_1)\cos(\omega t_2)\\ +&AB\{\cos(\omega t_1)\sin(\omega t_2)+\sin(\omega t_1)\cos(\omega t_2)\}\\ +&B^2\sin(\omega t_1)\sin(\omega t_2)\end{aligned}\]

Dans le calcul de la moyenne \(E\), le terme relatif à \(AB\) est nul. Il ne subsiste que deux les termes extrêmes pour lesquels on a de plus \(E(A^2)=E(B^2)=1\). Il vient après un calcul élémentaire : \[R_{xx}(t_1,t_2)=E\{X(t_1)X(t_2)\}=\cos\{\omega(t_2-t_1)\}\]

6. Fonction d’inter-corrélation

C’est la généralisation de la notion de corrélation étendue à deux fonctions différentes. La définition en découle : \[R_{xy}(t_1,t_2)=E\{X(t_1)~Y(t_2)\}\]

7. Action des opérateurs linéaires

L’idée repose sur le fait que l’opérateur \(E\) est permutable avec les opérateurs \(\int\) et \(d/dt\).

7.1. Intégration et dérivation

Pour l’intégration, on pose : \[Y(t)=\int_0^tX(u)~du\]

On a alors : \[m_y(t)=E\{Y(t)\}=\int_0^tE\{X(u)\}~du=\int_0^tm_x(u)~du\] Pour la dérivation, on pose : \[Y(t)=\frac{d}{dt}\{X(t)\}\]

On a alors : \[m_y(t)=\frac{d}{dt}E\{X(t)\}=\frac{d}{dt}\big\{m_x(t)\big\}\]

7.2. Application

On se place dans l’hypothèse d’une intégration. On recherche l’expression de la fonction d’auto-corrélation de \(Y=\int Xdt\), connaissant celle de \(X\) : \[\begin{aligned} &R_{yy}(t_1t_2)=E\{Y(t_1)~Y(t_2)\}=E\{\int_0^{t_1}X(t_1)~dt_1\cdot\int_0^{t_2}X(t_2)~dt_2\}\\ &R_{yy}(t_1t_2)=E\{\int_0^{t_1}\int_0^{t_2}X(t_1)~X(t_2)~dt_1~dt_2\}\end{aligned}\]

On a donc : \[R_{yy}=\int_0^{t_1}\int_0^{t_2}R_{xx}(t_1,t_2)~dt_1~dt_2\]

8. Somme de variables aléatoires

On pose : \[Z(t)=X_1(t)+X_2(t)\]

La relation aux moyennes est évidente : \[m_z(t)=m_{x_1}(t)+m_{x_2}(t)\]

De même : \[R_{zz}(t_1,t_2)=R_{x_1x_1}(t_1,t_2)+R_{x_1x_2}(t_1,t_2)+R_{x_2x_1}(t_1,t_2)+R_{x_2x_2}(t_1,t_2)\]

Si les deux variables sont décorrélées : \[R_{zz}(t_1,t_2)=R_{x_1x_1}(t_1,t_2)+R_{x_2x_2}(t_1,t_2)\]

9. Stationnarité

9.1. Stationnarité au sens strict

On dit qu’une fonction aléatoire \(X(t)\) est stationnaire au sens strict si toutes les propriétés statistiques (moments) sont invariantes pour tout changement de l’origine des temps \((t\rightarrow t+\tau )\). Cette notion est très restrictive et n’apporte aucun intérêt physique. On lui préfère la notion de stationnarité au sens large.

9.2. Stationnarité au sens large

On la désigne encore sous le nom de stationnarité d’ordre 2. En physique, le moment du premier ordre fixe un ordre de grandeur de X(t), c’est-à-dire une amplitude. Le moment d’ordre 2 a une signification énergétique. On s’intéresse à ces deux moments et on définit la stationnarité du deuxième ordre par : \[\begin{aligned} &E\{X(t)\}=m \quad \text{indépendante du temps }t\\ &\gamma(t_1,t_2)\quad \text{ne dépend que de l'écart temporel } ~ \tau=t_2-t_1\end{aligned}\]

Exemple

La fonction étudiée précédemment (\(A\) et \(B\) réduites) est stationnaire d’ordre 2 : \[\begin{aligned} &X(t)=A\cos(\omega t)+B\sin(\omega t)\\ &E(X)=E(A)\cos(\omega t)+E(B)\sin(\omega t)=0\\ &\gamma(t_1,t_2)=\cos\{\omega(t_2-t_1)\}=\cos(\omega\tau)\end{aligned}\]

10. Ergodisme

La connaissance de \(E\{X(t)\}\) implique qu’à l’instant \(t\), on observe toutes les valeurs possibles de \(X(t\)) et que l’on prenne la moyenne pondérée compte tenu des probabilités. Ceci n’est pas commode.

À l’observation simultanée d’un très grand nombre d’appareils identiques, on substitue un enregistrement sur un appareil et on détermine la moyenne dans le temps : \[m(T)=\frac{1}{T}\int_0^TX(t)~dt\]

Le processus \(X(t)\) est dit ergodique si on peut identifier les moyennes d’ensemble (ou moyennes stochastiques) et les moyennes temporelles. En réalité, la notion d’ergodisme est plus complexe. On la définit habituellement par (raisons physiques) : \[\begin{aligned} &m=E\{X(t)\}=\lim_{T\rightarrow\infty}\Bigl\{\frac{1}{T}\int_0^TX(t)~dt\Bigr\}\\ &\gamma(t_1,t_2)=E\{X(t)~X(t-\tau)\}=\lim_{T\rightarrow\infty}\Bigl\{\frac{1}{T}\int_0^TX(t)~X(t-\tau)~dt\Bigr\}\end{aligned}\]

11. Un exemple de processus ergodique

Nous allons montrer que le processus suivant (rencontré souvent en théorie du signal) est ergodique : \[\begin{aligned} &X(t)=\cos(\omega t+\phi)\\ &\phi=\text{variable aléatoire "équirépartie" sur l'intervalle } [0,2\pi]\end{aligned}\]

La répartition uniforme implique la densité de probabilité : \[f(\phi)=\frac{1}{2\pi}\]

Étude de l’ordre 1

Stochastique : \[E\{X(t)\}=\int_0^{2\pi}\frac{1}{2\pi}\cos(\omega t+\phi)~d\phi=0\]

Temporel : \[\begin{aligned} &E\{X(t)\}=\lim_{T\rightarrow\infty}\Bigl\{\frac{1}{T}\int_0^TX(t)~dt\Bigr\}=0\\ &\text{car} \ \int_0^T\cos(\omega t+\phi)~d\phi=0 \ \ \ \text{bornée.}\end{aligned}\]

Étude de l’ordre 2

Stochastique : \[\begin{aligned} &E\{X(t)~X(t-\tau)\}=\frac{1}{2\pi}\int_0^{2\pi}\cos(\omega t+\phi)\cos[(\omega(t-\tau)+\phi)]~d\phi \\ &E\{X(t)~X(t-\tau)\}=\frac{1}{2\pi}\Bigl\{\int_0^{2\pi}\frac{\cos(\omega\tau)}{2}+\int_0^{2\pi}\frac{\cos[2\omega(t+\phi)-\tau]}{2}~d\phi\Bigr\}\end{aligned}\]

La deuxième intégrale étant nulle (intégration de \(\cos\phi\) sur \([0,2\pi]\)) : \[E\{X(t)~X(t-\tau)\}=\frac{\cos\omega\tau}{2}\frac{1}{2\pi}\int_0^{2\pi}d\phi=\frac{\cos(\omega\tau)}{2}\]

Temporel : \[\begin{aligned} &\gamma(t_1,t_2)=E\{X(t)~X(t-\tau)\}=\lim_{T\rightarrow\infty}\Bigl\{\frac{1}{T}\int_0^TX(t)X(t-\tau)~dt\Bigr\}\\ &\gamma(t_1,t_2)=\lim_{T\rightarrow\infty}\Bigl\{\frac{1}{T}\int_0^T\frac{\cos(\omega\tau)}{2}~dt+\frac{1}{T}\int_0^T\frac{\cos[2\omega(t+\phi)-\tau]}{2}~dt\Bigr\}\end{aligned}\]

La deuxième intégrale étant nulle (intégrale en cosinus, bornée), il ne subsiste que la première dont la valeur est : \(\cos(\omega\tau/2)\).

En conclusion, il y a bien ergodisme, car : \[\begin{aligned} &E\{X(t)=0\}=0\\ &E\{X(t)~X(t-\tau)\}=\frac{\cos(\omega\tau)}{2}\end{aligned}\]