1. Fonctions périodiques. Séries de Fourier
Toute fonction périodique \(x(t)\) de période \(T\) peut s’écrire sous la forme d’une série :
\[\begin{aligned} x(t)&=\sum_{n=-\infty}^{+\infty} C_n~\exp\Big(j~2\pi~\frac{n}{T}~t\Big)\\ C_n&=\frac{1}{T}\int_{-T/2}^{+T/2} x(t)~\exp\Big(j~2\pi~\frac{n}{T}~t\Big)~dt\end{aligned}\]
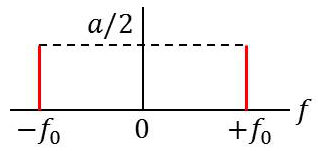On sait que le spectre en amplitude d’une fonction sinusoïdale \(s(t)=a~\cos(2\pi~f_0~t)\) se compose de deux raies symétriques : \[S(f)=\frac{a}{2}~\{\delta(f-f_0)+\delta(f+f_0)\}\]
On trouvera facilement pour le spectre en amplitude de \(x(t)\) : \[X(f)=\sum_{n=-\infty}^{+\infty} C_n~\delta\Big(f-\frac{n}{T}\Big)\]
Le spectre est un spectre de raies d’amplitude \(|C_n|\) régulièrement espacées de \(1/T\).
2. Fonctions apériodiques. Transformation de Fourier
Si la fonction \(x(t)\) n’est pas périodique, on peut toujours supposer qu’elle l’est en admettant que la période T devient infinie. Dans ces conditions, \(1/T~\rightarrow 0\) , l’espacement entre les raies diminue et le spectre devient un spectre continu. Donc si \(x(t)\) n’est pas périodique, on passe de sa représentation temporelle \(x(t)\) à sa représentation fréquentielle ou spectre \(X(f)\) au moyen de la transformation de Fourier. Cette transformation s’adapte à n’importe quelle fonction apériodique.
On rappelle les deux formules de transformation (directe et inverse) :
\[\begin{aligned} x(t)~~&\rightarrow~~X(f)=\int_{-\infty}^{+\infty} x(t)~\exp(-j~2\pi~f~t)~dt\\ X(f)~~&\rightarrow~~x(t)=\int_{-\infty}^{+\infty} X(f)~\exp(+j~2\pi~f~t)~df\end{aligned}\]
Une intégrale est d’ailleurs très utile en transformation de Fourier (ainsi que pour le calcul des probabilités) :
\[\begin{aligned} \int_{-\infty}^{+\infty}\exp(-a~x^2\pm 2~b~x+c)~dx&=\sqrt{\frac{\pi}{a}}~\exp(-\frac{a~c-b^2}{a})\qquad (a,~b,~c)\in\mathbb{R~,~C}\text{, mais}~~x\in\mathbb{R}\\ \int_0^{+\infty}\exp(-x^2)~dx&=\frac{1}{2}\int_{-\infty}^{+\infty} \exp(-x^2)~dx=\frac{\sqrt{\pi}}{2}\qquad (a=1~;~b=c=0)\end{aligned}\]
Remarque
D’une manière générale, \(X(f)\) est une quantité complexe que l’on peut mettre sous la forme : \[X(f)=|X(f)|~e^{j~\varphi(f)}\quad;\quad \varphi(f)=\arg[X(f)]\]
Si \(x(t)\) est une fonction réelle, \(X(f)\) possède la propriété de symétrie hermitienne : \[X(-f)=\overline{X(f)}\]
c’est-à-dire : \[\left\{ \begin{aligned} |X(-f)|&=|\overline{X(f)}|=|X(f)|\\ \arg[X(-f)]&=\arg\overline{X(f)}=-\arg[X(f)] \end{aligned} \right.\]
En conclusion, si \(x(t)\) est une fonction réelle, le module de \(X(f)\) est pair et la phase de \(X(f)\) est impaire.
3. Théorèmes
3.1. Théorème de Plancherel
On considère trois fonctions \(x(t),~y(t),~z(t)\) dont les spectres en fréquence sont respectivement \(X(f),~Y(f),~Z(f)\) : \[z(t)=x(t)~y(t)\quad\Rightarrow\quad Z(f)=X(f)\star Y(f)\]
Et réciproquement : \[z(t)=x(t)\star y(t)\quad\Rightarrow\quad Z(f)=X(f)~Y(f)\]
Ainsi, l’opération de convolution dans un espace devient un produit dans l’autre.
3.2. Théorème de Parseval
On considère deux fonctions (\(x(t),~y(t)\)) de spectres respectifs (\(X(f),~Y(f)\)). On peut écrire : \[\int_{-\infty}^{+\infty}x(t)~\overline{y(t)}~dt=\int_{-\infty}^{+\infty}X(f)~\overline{Y(f)}~df\]
En particulier : \[\int_{-\infty}^{+\infty}|x(t)|^2~dt=\int_{-\infty}^{+\infty}|X(f)|^2~df\]
Ainsi, les calculs peuvent-ils être menés dans l’espace des temps ou dans l’espace des fréquences selon la complexité des expressions dans un espace ou dans l’autre.
4. Transformées de Fourier les plus utiles
\[\begin{array}{r c l} \text{Espace temps} &\longleftrightarrow & \text{Espace fréquences} \\ x(t-a) &\longleftrightarrow &e^{-j~2\pi~f~a}~X(f) \\ x(t)~e^{j~2\pi~f_0~t} &\longleftrightarrow &X(f-f_0) \\ \delta(t) &\longleftrightarrow &1 \\ 1 &\longleftrightarrow &\delta(f) \\ e^{j~2\pi~f_0~t} &\longleftrightarrow &\delta(f-f_0) \\ \delta(t-t_0) &\longleftrightarrow &e^{-j~2\pi~f~t_0} \\ \cos(2\pi~f_0~t) &\longleftrightarrow &\{\delta(f-f_0)+\delta(f+f_0)\}/ 2 \\ \sin(2\pi~f_0~t) &\longleftrightarrow &j~\{\delta(f+f_0)-\delta(f-f_0)\}/ 2 \\ x(t)~\cos(2\pi~f_0~t) &\longleftrightarrow &\{X(f+f_0)+X(f-f_0)\}/ 2 \\ x(t)\star y(t) &\longleftrightarrow &X(f)~Y(f) \\ x(t)\star\overline{y(-t)} &\longleftrightarrow &X(f)~Y(-f) \\ {d^n}/{dt^n}[x(t)] &\longleftrightarrow &(j2\pi f)^n~X(f) \\ (-j~2\pi~t)^n~x(t) &\longleftrightarrow &{d^n}/{df^n}[X(f)] \end{array}\]
