1. Transformations unilatérales et bilatérales
Le calcul symbolique ou calcul opérationnel a été introduit par Heaviside pour simplifier la résolution de certains problèmes d’électricité et d’électronique par une manière de résolution systématique de certaines équations différentielles.
L’idée principale était de traiter l’opérateur de différentiation \(d/dt\) comme une quantité algébrique en posant \(p=d/dt\). De la sorte, si l’on a une fonction \(f(t)\) alors on pourra écrire, dans une première approche \(f'=p~f\).
Si \(Q(x)\) est un polynôme à coefficients constants, le polynôme \(Q(p)\) est bien défini.
Dans notre étude, nous nous placerons dans des conditions simples qui correspondent aux situations rencontrées en électronique et qui nous conduiront à limiter notre exposé à ce que l’on appelle la transformation unilatérale (intégrations dans un intervalle \([0,~+\infty]\)), par opposition à la transformation bilatérale (intégrations dans un intervalle \([-\infty,~+\infty]\)) beaucoup plus stricte sur le plan mathématique.
2. Définition simplifiée
À toute fonction \(f(t)\) nulle pour \(t<0\), on fait correspondre une fonction \(F(p)\) de la variable complexe \(p\) que l’on appelle transformée de Laplace de \(f(t)\) suivant l’expression : \[F(p)=\int_0^{\infty}e^{-p~t}~dt\]
On dit que \(F(p)\) est l’image de \(f(t)\), ce que l’on peut exprimer symboliquement par : \[F(p)~\subset~f(t)\]
Alors, \(f(t)\) est l’original de \(F(p)\) par une transformation inverse que l’on peut exprimer symboliquement par : \[f(t)~\supset~F(p)\]
Nous n’abordons pas ici les problèmes de convergence d’intégrales (abscisses de convergence) que nous supposons résolus et respectés.
3. Propriétés principales
3.1. Somme de fonctions
Considérons la fonction : \[f(t)=f_1(t)+f_2(t)\]
Du fait de la linéarité dans l’intégration : \[F(p)=F_1(p)+F_2(p)\]
3.2. Dérivation
Reprenons la définition : \[F(p)=\int_0^{\infty}e^{-p~t}~f(t)~dt\]
Intégrons par parties : \[pF(p)=\big\{-e^{-p~t}~f(t)\big\}_0^{\infty}+\int_0^{\infty} e^{-p~t}~f'(t)~dt\]
On peut écrire, de manière intuitive, que : \[e^{-p~t}~f(t)=\frac{f(t)}{1+p~t+\cfrac{p^2~t^2}{2}+\dots}\]
Compte tenu de la restriction imposée à \(f(t)\), la relation d’intégration par parties peut s’interpréter comme : \[f'(t)~\supset~p~F(p)-f(0^+)\]
Très fréquemment, les conditions physiques initiales font que \(f(0^+)=0\), ce qui fait dire parfois abusivement que l’image de la fonction dérivée est obtenue en multipliant par \(p\) l’image de référence.
Bien entendu le processus se généralise et l’on peut alors écrire à l’ordre 2 : \[f''(t)~\supset~p^2~F(p)-p~f(0^+)-f'(0^+)\]
et ainsi de suite.
3.3. Intégration
Par un mode de calcul analogue à celui du paragraphe précédent, on montrerait que : \[\int_a^t f(s)~ds~\supset~\frac{F(p)}{p}-\frac{1}{p}\int_0^a f(s)~ds\qquad(a>0)\]
dans le cas particulier où : \[\int_a^t f(s)~ds~\supset~\frac{F(p)}{p}\]
3.4. Produit de convolution
Nous énoncerons directement le résultat sans démonstration, compte tenu de la similitude de la transformation de Laplace avec la transformation de Fourier.
Par analogie avec le théorème de Plancherel, nous aurons le résultat remarquable suivant : \[f~\supset~F~\text{ et }~g~\supset~G\qquad\Rightarrow\qquad (f\star g)~\supset~F~G\]
4. Théorème de la valeur initiale (et finale)
Étant donnée la transformée \(F(p)\) de la fonction \(f(t)\) que l’on ne connaît pas, il est souvent intéressant de déterminer les valeurs que prend cette fonction aux instants zéro et infini sans qu’il soit nécessaire de la calculer explicitement.
Théorème de la valeur initiale : \[f(0)=lim_{p~\rightarrow~\infty}~\{p~F(p)\}\]
Théorème de la valeur finale : \[f(\infty)=lim_{p~\rightarrow~0}~\{p~F(p)\}\]
5. Translation et théorème du retard
En utilisant toujours les propriétés de l’intégration, on démontre que :
\[\begin{aligned} &e^{-\lambda~t}~f(t)~\supset~F(p+\lambda)\\ &Y(t-\lambda)~f(t)~\supset~e^{-\lambda~p}~F(p)\end{aligned}\]
6. Transformées les plus usuelles
Les fonctions sont toujours exprimées avec pondération par la fonction échelon de façon à garantir une valeur nulle pour les \(t < 0\). Elles sont données ici à titre indicatif sachant qu’en règle générale on possède des tables de transformées classiques sans avoir à les recalculer.
\[\begin{aligned} Y(t)~&\supset~\frac{1}{p} &&\text{Intégration élémentaire}\\ Y(t)~t^n~&\supset~\frac{n!}{p^{n+1}} &&\text{Faisant n=0, on retrouve le précédent résultat.}\\ Y(t)~e^{a~t}~&\supset~\frac{1}{p-a} &&\text{Application du théorème du retard à la première}\\ Y(t)~\cos(\omega~t)~&\supset~\frac{p}{p^2+\omega^2} &&\mathcal{R}\{\text{image de}~Y(t)~e^{j~\omega~t}~\}\\ Y(t)~\sin(\omega~t)~&\supset~\frac{\omega}{p^2+\omega^2} &&\mathcal{R}\{\text{image de}~Y(t)~e^{j~\omega~t}~\}\end{aligned}\]
7. Quelques indications de calcul
7.1. Fonction en escalier
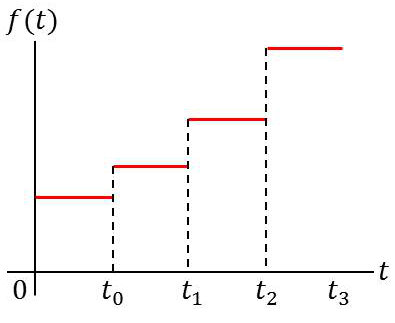 On exprime \(f(t)\) comme une somme de fonctions échelons retardés : \[f(t)=a_0~\{Y(t)-Y(t-t_0)\}+a_1~\{Y(t)-Y(t-t_1)\}+\dots\]
On exprime \(f(t)\) comme une somme de fonctions échelons retardés : \[f(t)=a_0~\{Y(t)-Y(t-t_0)\}+a_1~\{Y(t)-Y(t-t_1)\}+\dots\]
On applique le théorème de translation : \[Y(t)~\supset~\frac{1}{p}\quad;\quad Y(t-\lambda)~\supset~\frac{e^{-\lambda~p}}{p}\]
et on réalise la combinaison linéaire des images des fonctions composant la somme.
7.2. Fonction porte périodique
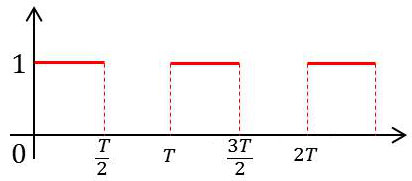 On calcule l’image de la première porte (intégration entre \([0,~T/2]\) et on considère les autres à partir d’une translation (\(T,~2~T\dots\)).
On calcule l’image de la première porte (intégration entre \([0,~T/2]\) et on considère les autres à partir d’une translation (\(T,~2~T\dots\)).
La première image sera l’image de base multipliée par 1 ; les autres seront obtenues par les multiplications respectives \(e^{-p~T},~e^{-2~p~T}\dots\)
L’image définitive sera l’image de de base multipliée par la somme : \[1+e^{-p~T}+e^{-2~p~T}+\cdots\]

