1. Équation différentielle
Soit à résoudre par exemple l’équation : \[a~z''+b~z'+c=h~e^{j~\omega~x}\]
Nous faisons l’hypothèse que \(z\in\mathbb{R}\).
Le formalisme de Laplace permet d’établir les correspondances suivantes :
\[\begin{aligned} z~&\subset~Z\\ z'~&\subset~p~Z-Z_0\qquad;\qquad z''\subset p^2~Z-p~Z_0-Z'_0\\ h~e^{-j~\omega~x}~&\subset~\frac{h}{p-j~\omega}\end{aligned}\]
D’où l’équation algébrique à résoudre : \[(a~p^2+b~p+c)~Z(p)-Z_0~(a~p+b)-a~Z'_0=\frac{h}{p-j~\omega}\]
Dans l’hypothèse de conditions initiales nulles : \[(a~p^2+b~p+c)~Z(p)=\frac{h}{p-j~\omega}\]
On en déduit \(Z(p)\), puis l’original \(z(t)\) en utilisant des tables de transformées.
Il est naturellement indispensable de présenter \(Z(p)\) sous une forme qui permette de les utiliser le plus commodément possible.
2. Système différentiel
Pour faciliter l’exposé, nous raisonnerons sur l’exemple qui suit : \[\left\{ \begin{aligned} &x'=a~y+f(t)\\ &y'=-a~x+g(t) \end{aligned} \right.\]
On recherche une solution qui s’annule pour \(t = 0\).
Appliquons la transformation de Laplace : \[\left\{ \begin{aligned} &p~X-a~Y=F\\ &a~X+p~Y=G \end{aligned} \right.\]
dont la solution est : \[X=\frac{p~F+a~G}{p^2+a^2}\qquad;\qquad Y=\frac{-a~F+p~G}{p^2+a^2}\]
On remarque que :
\[\begin{aligned} \frac{p~F}{p^2+a^2}~~&:~~\text{produit de deux fonctions aux originaux}~~[f(t),~\cos(at)]\\ \frac{a~G}{p^2+a^2}~~&:~~\text{produit de deux fonctions aux originaux}~~[g(t),~\sin(at)]\end{aligned}\]
On aura donc en original deux produits de convolution :
\[\begin{aligned} &\frac{p~F}{p^2+a^2}~\supset~\int_0^t\cos~a(t-s)~f(s)~ds\\ &\frac{a~G}{p^2+a^2}~\supset~\int_0^t\sin~a(t-s)~g(s)~ds\end{aligned}\]
On obtient, tous calculs faits :
\[\begin{aligned} x(t)&=\Big\{\int_0^tf(s)~\cos~a(t-s)+\int_0^tg(s)~\sin~a(t-s)\Big\}~ds\\ y(t)&=\Big\{\int_0^t-f(s)~\sin~a(t-s)+\int_0^tg(s)~\cos~a(t-s)\Big\}~ds\end{aligned}\]
3. Application à l’électronique
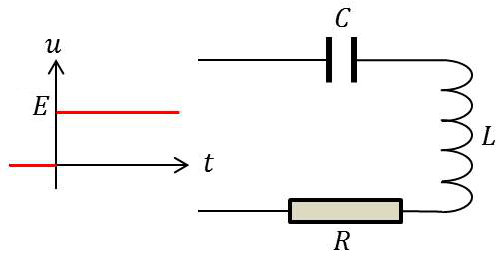 Considérons le circuit \(RLC\) ci-contre.
Considérons le circuit \(RLC\) ci-contre.
À l’instant \(t = 0\), on introduit une force électromotrice constante \(E\).
On recherche l’expression du courant \(i(t)\).
Passons aux notations symboliques :
\[\begin{aligned} &U(p)=\frac{E}{p}\\ &Z(p)=L~p+R+\frac{1}{C~p}\end{aligned}\]
Pour l’expression du courant : \[I(p)=\frac{U(p)}{Z(p)}=\frac{U(p)}{Z(p)}=\frac{E}{L~p^2+R~p+\cfrac{1}{C}}\]
En posant (racines du trinôme) : \[p_{1,2}=-\frac{R}{2~L}\pm j~\sqrt{\frac{1}{L~C}-\frac{R^2}{4~L^2}}\]
On peut écrire : \[i(t)~\supset~\frac{E}{L~(p_2-p_1)}~\Big\{\frac{1}{p-p_2}-\frac{1}{p-p_1}\Big\}\]
On connaît les originaux (tables) : \[\frac{1}{p-p_1}~\supset~e^{-p_1~t}\quad;\quad\frac{1}{p-p_2}~\supset~e^{-p_2~t}\]
Enfin, en posant : \[\alpha=\sqrt{\frac{1}{L~C}-\frac{R^2}{4~L^2}}\]
Il vient : \[i(t)=\frac{E}{\alpha~L}~\exp\Big(-\frac{R}{L}~t\Big)~\sin(\alpha~t)\]

