1. Définition
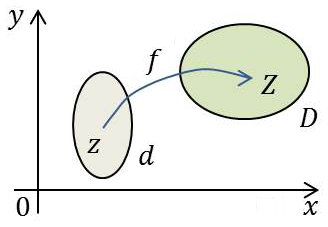Considérons dans le plan complexe les deux nombres d’affixes respectives \(z\) et \(Z\), tels que : \[z=x+i~y\quad z\in d\qquad\rightarrow\quad Z=X+i~Y\quad Z\in D\]
Au couple de réels (\(x,~y\)) correspond le couple de réels (\(X,~Y\)) au moyen d’une transformation biunivoque : \[Z=f(z)\qquad\text{ou}\qquad X=P(x,~y)\quad;\quad Y=Q(x,~y)\]
Exemples
Prenons une fonction simple \(Z=z^2\).
On peut l’écrire sous la forme : \[X+i~Y=(x+i~y)^2=x^2+2~i~x~y+(i~y)^2=x^2-y^2+2~i~x~y\]
En identifiant : \[X=x^2-y^2\quad;\quad Y=2~x~y\]
Inversement, si on se donne : \[X=x\qquad;\qquad Y=2~y\]
on peut écrire : \[X+iY=x+2~i~y=(x+i~y)+i~y\]
Remarquant que : \[2~i~y=(x+i~y)-(x-i~y)=z-\overline{z}\]
on peut donc écrire : \[Z=f(z)=z+\frac{1}{2}(z-\overline{z})=\frac{3}{2}z-\overline{z}\]
2. Notion de dérivée
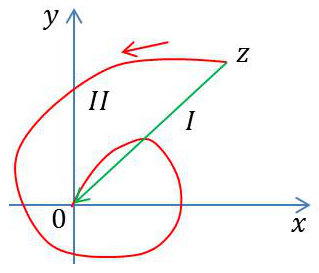La notion de dérivée est délicate, car il ne s’agit pas de calculer une limite du type traditionnel : \[lim\Big(\frac{\Delta y}{\Delta x}\Big)\qquad\text{quand}\quad \Delta x\rightarrow 0\]
La figure montre en effet que l’on peut passer de l’affixe \(z\) à l’affixe \(0\) par une infinité de chemins et l’on n’est pas sûr, pour un chemin donné, d’obtenir un résultat unique pour : \[lim\Big(\frac{\Delta f}{\Delta z}\Big)\qquad\text{quand}\quad \Delta z\rightarrow 0\]
3. Dérivation selon Cauchy
Si, quand \(\Delta z\rightarrow 0\), d’une manière quelconque, le quotient précédent a une limite finie, la fonction complexe a une dérivée, la fonction est alors dite analytique.
La condition nécessaire et suffisante d’existence en un point \(M\) est donnée par les relations aux dérivées partielles de Cauchy : \[P'_x=Q'_y\qquad;\qquad P'_y=-Q'_x\]
D’où l’expression de la dérivée de \(f(z)\) par rapport à \(z\) : \[f'(z)=P'_x+i~Q'_y=P'_y-i~Q'_x\]
Si \(f(z)\) est analytique en tout point d’un domaine \(\mathcal{R}\) et si \(f'(z)\) est continue dans ce domaine, on dit que \(f(z)\) est analytique et régulière.
Réciproquement :
Si \(f(z)=P+i~Q\) est telle que \(P\) et \(Q\) admettent des dérivées premières continues dans ce domaine, liées par les conditions de Cauchy, la fonction est analytique et régulière dans ce domaine.
4. Fonctions élémentaires
4.1. Polynômes en z
Le résultat suivant, non démontré, est intuitif (n entier) : \[f(z)=z^n\qquad;\qquad f'(z)=n~z^{n-1}\]
donc tout polynôme en \(z\) sera une fonction analytique.
4.2. Fonction exponentielle
La fonction \(e^{z}\) est-elle analytique ? On sait que : \[e^z=e^{x+i~y}=e^x~(\cos y+\sin y)\]
On pose naturellement : \[P=e^x~\cos y\qquad;\qquad Q=e^x~\sin y\]
D’où le résultat intuitif : \[f'(z)=P'_x+i~Q'_y=e^z\]
4.3. Application aux fonctions circulaires
On pose : \[\cos z=\frac{1}{2}~(e^{i~z}+e^{-i~z})\qquad;\qquad \sin z=\frac{1}{2~i}(e^{i~z}-e^{-i~z})\]
Les fonctions \(\cos(z)\) et \(\sin(z)\) définies dans tout le plan complexe sont analytiques et régulières.
Déterminons les zéros de ces fonctions, en considérons la fonction \(\cos(z)\). \[e^{i~z}+e^{-i~z}=0\quad\text{ou}\quad e^{2~i~z}+1=0\quad\text{ou}\quad e^{2~i~z}=-1\]
Exprimé autrement : \[e^{2~i~(x+i~y)}=e^{2~i~x}~e^{-2~y}=-1=e^{i~\pi}\]
On a donc : \[e^{-2~y}=1\]
Il s’ensuit que : \[y=0\qquad;\qquad 2~x=\pi+2~k~\pi\qquad\text{ou encore}\quad x=\frac{\pi}{2}+k~\pi\]
Un calcul analogue donnerait pour \(\sin(z)\) \[y=0\qquad;\qquad x=k~\pi\]
Pour les deux fonctions, on obtient des zéros réels.
4.4. Application aux fonctions hyperboliques
On pose : \[\cosh(z)=\frac{1}{2}~(e^z+e^{-z})\qquad;\qquad \sinh(z)=\frac{1}{2}~(e^z-e^{-z})\]
Des calculs analogues aux précédents pour la détermination des zéros donneraient :
\[\begin{aligned} &\text{pour}~\cosh(z)~:\qquad x=0\qquad y=\frac{\pi}{2}+k~\pi\\ &\text{pour}~\sinh(z)~:\qquad x=0\qquad y=k~\pi\end{aligned}\]
Les zéros sont donc imaginaires purs.
4.5. Formules d’addition
Le résultat est intuitif : \[e^{i~(z_1+z_2)}=e^{i~z_1}~e^{i~z_2}\]
Pour le démontrer, on pose : \[e^{i~z}=\cos z+i~\sin z\qquad;\qquad e^{-i~z}=\cos z-i~\sin z\]
On a alors:
\[\begin{aligned} &e^{i~(z_1+z_2)}=\cos(z_1+z_2)+i~\sin(z_1+z_2)\\ &e^{i~(z_1+z_2)}=(\cos z_1+i~\sin z_1)~(\cos z_2+i~\sin z_2)=e^{i~z_1}~e^{i~z_2}\end{aligned}\]
On retrouve les formules d’addition de la trigonométrie. Il en serait de même pour les fonctions hyperboliques.
