1. Position du problème

On considère une particule qui n’est soumise à aucune force sauf en une région très petite de l’espace.

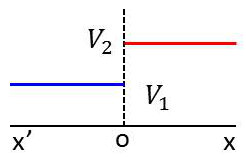D’un côté de cette région, elle possède une énergie potentielle constante \(V_1\) et de l’autre une énergie potentielle constante \(V_2\). Entre les deux, son énergie potentielle varie rapidement de \(V_1\) à \(V_2\). À la limite, nous pouvons supposer que l’épaisseur de cette région est infiniment petite et qu’au point \(O\), l’énergie potentielle passe brusquement de \(V_1\) à \(V_2\).

Pour fixer les idées, nous supposerons que la particule se déplace de la gauche vers la droite : \(V_1\) représente donc son énergie potentielle pour \(x < 0\) et \(V_2\) son énergie potentielle pour \(x > 0\).

L’action d’une telle barrière de potentiel sur le mouvement de la particule dépend de son énergie totale \(E\) qui est par hypothèse supérieure à \(V_1\), sinon la particule n’aurait pas d’énergie cinétique et ne pourrait se déplacer :

\[\begin{aligned} &V_2<V_1 && &&\text{La particule est accélérée.} &&E_c=E-V \\ &V_2>V_1 &&E>V_2 &&\text{La particule est ralentie.} \\ & &&E<V_2 &&\text{La particule est réfléchie.}\end{aligned}\]

Si au lieu de considérer une particule, on considère un faisceau de particules identiques animées de la même vitesse (donc de même énergie \(E\)), nous pouvons dire que, dans le premier et le second cas, elles traversent toutes la discontinuité \((R = 0~et~T = 1)\) alors que dans le troisième elles sont toutes réfléchies \((R= 1~et~T = 0)\) et on n’en trouve aucune de l’autre côté de la discontinuité.

1.1. Conditions pour \(\Psi\) à la limite

Revenons à présent à la fonction d’onde \(\Psi\) définie et étudiée précédemment (équation de Schrödinger). Celle-ci doit être partout continue. On doit donc avoir : \[\Psi_1(0)=\Psi_2(0)\qquad\text{et}\qquad\Psi'_1(0)=\Psi'_2(0)\]

Elle doit également être régulière, c’est-à-dire partout finie.

1.2. Formes de la fonction \(\Psi\)

Reprenons l’équation de Schrödinger : \[\frac{\partial^2\Psi}{\partial t^2}+(E-V)~\frac{2m}{\hbar}~\Psi=0\]

Introduisons les paramètres : \[p^2=2m~(E-V)\qquad;\qquad\lambda=\frac{h}{p}=2\pi~\frac{h}{p}\]

On peut écrire indifféremment :

\[\begin{aligned} &\frac{\partial^2\Psi}{\partial x^2}+\frac{4\pi^2}{\lambda^2}~\Psi=0\\ &\frac{\partial^2\Psi}{\partial x^2}+\frac{p^2}{\hbar^2}~\Psi=0\end{aligned}\]

Elles conduisent aux solutions :

\[\begin{aligned} &\Psi=A~\exp(-j\frac{2\pi}{\lambda}x)+\Psi=A~\exp(+j\frac{2\pi}{\lambda}x)\\ &\Psi=A~\exp(-j\frac{p}{\hbar}x)+\Psi=A~\exp(+j\frac{p}{\hbar}x)\end{aligned}\]

2. Coefficients de réflexion et de transmission

Pour alléger l’écriture, on posera : \[k=\frac{2\pi}{\lambda}=\frac{p}{\hbar}\]

On désignera par \(r\) et \(t\) les coefficients de réflexion et de transmission en amplitude.

2.1. Premier cas : \(E>V_2\)

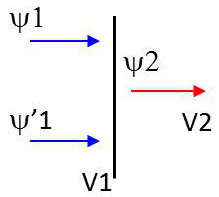Ce cas correspond à : \[p_1\in\mathbb{R}\quad;\quad~p_2=\sqrt{2m~(E-V_2)}\in\mathbb{R}\]

• Onde incidente : \( \Psi_1=\Psi_0~\exp(jk_1x) \)

• Onde réfléchie : \( \Psi'_1=r~\Psi_0~\exp(-jk_1x) \)

• Onde transmise : \( \Psi_2=t~\Psi_0~\exp(jk_2x) \)

Écrivons les équations de continuité :

\[\begin{aligned} \Psi_1(0)+\Psi'_1(0)&=\Psi_2(0) & 1+r&=t\\ \Big[\frac{d\Psi_1}{dx}\Big]_0+\Big[\frac{d\Psi'_1}{dx}\Big]_0&=\Big[\frac{d\Psi_2}{dx}\Big]_0 & k_1~(1-r)&=k_2~t\end{aligned}\]

La résolution du système \((r,~t)\) donne des résultats identiques aux formules de Fresnel dans les ondes électromagnétiques.

2.2. Deuxième cas : \(E<V_2\)

Ce cas correspond à \(p_2\in\mathbb{C}\), soit \(k_2=jk'_2\).

On remarque alors que : \[r~\frac{k_1-jk'_2}{k_1+jk'_2}\qquad\text{donc}\qquad~|r|=1\]

Car les deux termes de la fraction sont conjugués. Physiquement, cela signifie qu’il y a réflexion totale.

On remarque que l’onde transmise est de la forme : \[\Psi_2=t~\Psi_0~\exp(-k'_2~x)\]

La partie exponentielle s’annule rapidement quand \(x\) augmente. Ce phénomène rejoint celui de l’onde évanescente dans les ondes électromagnétiques.

Remarque

La probabilité pour une particule d’aller à droite est \(\Psi_1\Psi_1^*\)

La probabilité d’aller à gauche étant alors \(\Psi'_1{\Psi'_1}^*\).

La probabilité de réflexion est alors : \[R=r~r^*=\frac{\Psi'_1~{\Psi'_1}^*}{\Psi_1~\Psi_1^*}\]

Nous faisons le même raisonnement pour le calcul de \(T\), mais comme on passe du milieu (1) au milieu (2) la vitesse de propagation a changé.

Comme cela a été vu pour les ondes électromagnétiques, on doit écrire : \[T=t~t^*~\frac{v_2}{v_1}\]

Or, on a : \[p=m~v\quad\Rightarrow\quad~v=\frac{p}{m}\]

On pourra donc écrire : \[T=t~t^*~\frac{v_2}{v_1}=\frac{\Psi_2~\Psi_2^*}{\Psi_1~\Psi_1^*}\]

3. Effet tunnel

Considérons maintenant fois deux discontinuités de potentiel, avec les milieux extrêmes identiques.

La longueur de la barrière de potentiel à franchir est \(x_0\). On désigne par \(r\) le coefficient de réflexion à l’entrée de la barrière et par \(t\) le coefficient de transmission à la sortie de la barrière.

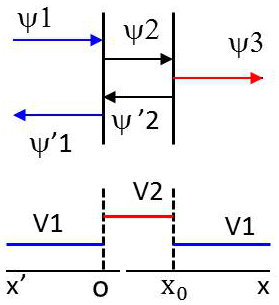On écrira (\(\alpha\) et \(\beta\) étant des coefficients secondaires) :

Dans le milieu (1) : \[\Psi_1+\Psi'_1=\Psi_0~\exp(j2\pi x/\lambda_1)+r~\Psi_0~\exp(-j2\pi x/\lambda_1)\]

Dans le milieu (2) : \[\Psi_2+\Psi'_2=\alpha~\Psi_0~\exp(j2\pi x/\lambda_2)+\beta~\Psi_0~\exp(-j2\pi x/\lambda_2)\]

Dans le milieu (3) \[\Psi_3=t~\Psi_0~\exp(j2\pi x/\lambda_1)\]

En dérivant les relations par rapport à la variable x : \[\begin{aligned} \frac{d}{dx}(\Psi_1+\Psi'_1)&=j\frac{2\pi}{\lambda_1}~\Psi_0~\{\exp(j2\pi x/\lambda_1)-r~\exp(-j2\pi x/\lambda_1)\} \\ \frac{d}{dx}(\Psi_2+\Psi'_2)&=j\frac{2\pi}{\lambda_2}~\Psi_0~\{\alpha~\exp(j2\pi x/\lambda_2)-\beta~\exp(-j2\pi x/\lambda_2)\}\\ \frac{d}{dx}(\Psi_3)&=j\frac{2\pi}{\lambda_1}~\Psi_0~\{t~\exp(j2\pi x/\lambda_1)\} \end{aligned}\]

Les équations de continuité à la première barrière de potentiel \((x = 0)\) s’écrivent :

\[\begin{aligned} 1+r&=\alpha+\beta\\ \frac{1}{\lambda_1}~(1-r)&=\frac{1}{\lambda_2}~(\alpha-\beta)\end{aligned}\]

Les équations de continuité à la deuxième barrière de potentiel \((x = x_0)\) s’écrivent, en allégeant l’écriture avec \(A=\exp(j2\pi~x_0/\lambda_2)\) et \(t'=t~\exp(j2\pi~x_0/\lambda_1)\) :

\[\begin{aligned} \alpha~A+\frac{\beta}{A}&=t'\\ \frac{1}{\lambda_2}~(\alpha~A-\frac{\beta}{A})&=\frac{1}{\lambda_1}~t'\end{aligned}\]

Du fait que les deux milieux extrêmes sont identiques, la probabilité de traverser la barrière de potentiel est : \[T=t~t^*=t'~t'^*\]

Nous supposerons que :

\[\begin{aligned} E>V_1~~\Rightarrow~~\lambda_1\in\mathcal{R}&\qquad\text{car}~~\lambda_1=\frac{h}{2m~(E-V_1)}=\frac{h}{p_1}\\ E<V_2~~\Rightarrow~~\lambda_2\in\mathcal{J}&\qquad\text{car}~~\lambda_2=\frac{h}{2m~(V_2-E)}=\frac{\lambda'_2}{j}\end{aligned}\]

Les équations de continuité s’écriront alors : \[[1]\left\{ \begin{aligned} &1+r=\alpha+\beta &&(1) \\ &1-r=j\frac{\lambda_1}{\lambda'_2}~(\alpha-\beta) &&(2) \end{aligned} \right. \qquad\qquad [2]\left\{ \begin{aligned} &\alpha~A+\frac{\beta}{A}=t' &&(3)\\ &\alpha~A-\frac{\beta}{A}=-j\frac{\lambda'_2}{\lambda'_1}~t' &&(4) \end{aligned} \right.\]

Or, on sait que \(A\varpropto t'\) et l’équation (3) ne sera satisfaite que si \(\alpha A\varpropto\cfrac{\beta}{A}\), c’est-à-dire du même ordre de grandeur : \[A=\exp(j\frac{2\pi}{\lambda_2}~x_0)=\exp(-\frac{2\pi}{\lambda'_2}~x_0)\]

Si \(x_0\) est assez grand, alors \(A\ll1\). Et comme \(\alpha~A~\varpropto~\beta/A\), c’est-à-dire : \(\alpha~\varpropto~\beta/A^2\). Ainsi \(\alpha>>1\).

Le système [1] pourra s’écrire (en négligeant \(\beta\) par rapport à \(\alpha\)) : \[\left\{ \begin{aligned} 1+r&=\alpha\\ 1-r&=j\frac{\lambda_1}{\lambda'_2}~\alpha \end{aligned} \right. \qquad\Rightarrow\qquad r=\frac{1-j\lambda_1/\lambda'_2}{1+j\lambda_1/\lambda'_2}\]

En faisant (1) + (2) : \[\alpha=\frac{2}{1+j\lambda_1/\lambda'_2}\]

En faisant (3) + (4) : \[2\alpha A=t'(1-j\lambda_1/\lambda'_2)=\frac{4A}{1+j\lambda_1/\lambda'_2}\]

On a donc : \[t'=\frac{4A}{(1-j\lambda_1/\lambda'_2)~(1+j\lambda_1/\lambda'_2)}=\frac{4A}{2+j\Big(\cfrac{\lambda_1}{\lambda'_2}-\cfrac{\lambda_2}{\lambda'_1}\Big)}\]

Par suite (tous calculs faits) : \[T=\frac{16~\exp\Big(-\cfrac{4\pi x_0}{\lambda'_2}\Big)}{4-\Big(\cfrac{\lambda_1}{\lambda'_2}-\cfrac{\lambda_2}{\lambda'_1}\Big)^2}\]

Puits de potentiel

L’étude est la même que la précédente, à cette différence près que \(V_2<V_1\), d’où le nom de puits de potentiel.

4. Effet tunnel. Mise en évidence

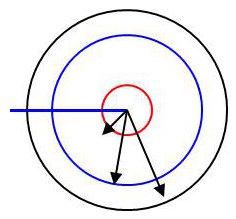Nous allons examiner le problème du pouvoir des pointes qui caractérise l’extraction des électrons dans les métaux.

Entre deux électrodes circulaires \([r,~R]\), on établit une différence de potentiel \(U\).

On considère la sphère intermédiaire \([r <\rho< R]\) et on étudie le flux du vecteur \(\overrightarrow{E}\) à travers ces sphères :

\[d\Phi=\overrightarrow{E}\centerdot\overrightarrow{n}~ds\quad\Rightarrow\quad r^2~E_0=\rho^2~E=R^2~E_1\]

Par suite : \[E=E_0~\frac{r^2}{\rho^2}=E_1~\frac{R^2}{\rho^2}\]

On sait que : \[\int_r^R E_0~\frac{r^2}{\rho^2}~d\rho=E_0~r-E_0~\frac{r^2}{R}\]

Le second terme étant négligeable par rapport au premier : \[U=E_0~r\quad\Rightarrow\quad r=\frac{U}{E_0}\quad;\quad E_0=\frac{U}{r}\]

Ainsi, en prenant les valeurs \(U=5~V\) et \(E_0=10^8~V/m\), on obtient la valeur \(d=0,5~nm\). Si la barrière n’a que 0,5 nm d’épaisseur, les électrons peuvent sortir par effet tunnel. De plus, on peut observer l’image de la pointe agrandie de \(R/r\) sur un écran fluorescent.

Un tel dispositif constitue un microscope à émission de champ (mis en œuvre la première fois par Muller).

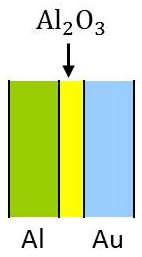
On peut considérer l’autre exemple schématisé ci-contre.

On donne les valeurs \(e=5~nm~;~U=5~V~;~E=U/e=10^7~V/cm\). Par effet tunnel, on observe un mouvement d’électrons du matériau \(Al\) vers le matériau \(Au\).

Cet exemple est encore l’une des manifestations de la propagation ondulatoire des particules.