1. Oscillateur harmonique en théorie classique
Soit une particule éloignée de \(x\) de sa position d’équilibre et dont la force de rappel est : \[f=-k~x\]
L’équation du mouvement est exprimée par l’équation différentielle : \[m~\ddot{x}=-k~x\]
La solution est de la forme : \[x=x_0~\cos(\omega~t+\varphi)\qquad\text{avec}\quad\omega^2=\frac{k}{m}\]
Son énergie cinétique à l’instant \(t\) est : \[E_c=\frac{1}{2}~m~v^2=\frac{1}{2}~m~\omega^2~x_0^2~\sin^2(\omega~t+\varphi)\]
Son énergie potentielle est : \[E_p=\int_0^x f~dx=\frac{k}{2}~x^2=\frac{1}{2}~m~\omega^2~x_0^2~\cos^2(\omega~t+\varphi)\]
L’énergie totale est une constante : \[W=E_p+E_c=\frac{1}{2}~m~\omega^2~x_0^2=\frac{k}{2}~x_0^2\]
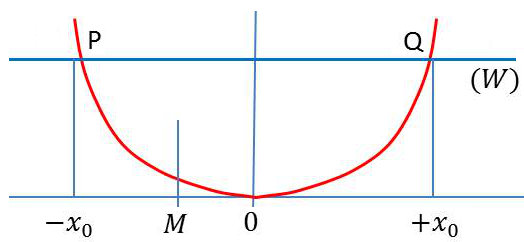 La représentation graphique de l’énergie potentielle est une parabole alors que celle de l’énergie totale est une droite.
La représentation graphique de l’énergie potentielle est une parabole alors que celle de l’énergie totale est une droite.
Pour un point \(M\) situé entre \(P\) et \(Q\) : \[W>E_p\quad;\quad E_c=W-E_p>0\]
Pour un point \(M\) situé en dehors de \(PQ\), on trouverait que \(E_c<0\), ce qui est bien sûr absurde.
En mécanique classique, la probabilité de trouver une particule au-delà de \([-x_0~,~+x_0]\) est strictement nulle, sinon son énergie cinétique serait négative.
2. Oscillateur harmonique en mécanique ondulatoire
Reprenons l’équation de Schrödinger : \[-\frac{\hbar^2}{2m}~\Delta\Psi+E_p~\Psi=W~\Psi\]
Elle admet une solution \(\Psi\) telle que l’on ait : \[\int_{-\infty}^{+\infty} \Psi~\Psi^*dx=1\]
Cette intégrale représente la probabilité de trouver une particule quelconque quelque part sur l’axe des abscisses.
On démontre que \(\Psi\) n’est mesurable que si : \[W=(n+\frac{1}{2})~h~\nu_0\quad;\quad \nu_0=\frac{1}{2\pi}~\sqrt{\frac{k}{m}}\]
En mécanique quantique, il est par contre possible de trouver la particule en un point où \(E_p>W\), c’est-à-dire que \(E_c<0\) (cf. effet tunnel).
3. Principe de correspondance de Bohr
Les résultats de la mécanique classique et de la mécanique quantique convergent lorsque \(n\rightarrow\infty\) .
L’oscillateur harmonique ne peut émettre que des photons de fréquence \(\nu_0\), donc d’énergie \(h\nu_0\), donc \(n\) ne peut varier que d’une unité à la fois.
C’est-à-dire que \(\Delta n=\pm 1\), le signe "+" correspondant à une émission et le signe "–" à une absorption.
Probabilité d’émission
Pendant le temps \(\Delta t\), l’oscillateur a une probabilité \(p~\Delta t\) d’émettre un photon d’énergie \(h\nu_0\). S’il y a \(N\) oscillateurs, l’énergie totale émise pendant \(\Delta t\) sera \(N~p~\Delta t~\nu_0\).
En mécanique classique, \(P\) étant la puissance rayonnée par un oscillateur, l’énergie totale pendant le temps \(\Delta t\) sera \(N~P~\Delta t\).
Le principe de correspondance veut que les deux résultats soient identiques.
On a par suite : \[p=\frac{P}{h~\nu_0}\]
Si l’on envoie un photon \(\nu_0\) sur l’oscillateur quantique, \(n\rightarrow n+1\).
Mais si l’on envoie \(2\nu_0\), on n’obtiendra pas \(n\rightarrow n+2\) et l’oscillateur ne réagira pas.
On aura la règle de sélection \(\Delta n=\pm 1\).
4. Classification des spectres
Une lampe à vapeur de mercure par exemple émet des raies \(\lambda\) bien définies ; la spectroscopie étudie les \(\lambda\) émises par une lampe ou absorbées par un corps. On distingue donc les spectres d’émission et les spectres d’absorption.
Cette étude est étroitement liée à la détermination des niveaux d’énergie.
4.1. Spectre en émission
Il existe dans les atomes ou les molécules des oscillateurs en général quantifiés, la particule ne pouvant occuper que certains niveaux d’énergie.
Le niveau le plus bas est dit fondamental ; les autres correspondant à un niveau d’excitation.
Sous l’action d’un chauffage ou d’un champ électrique, la particule passe dans un niveau excité ; elle a alors trop d’énergie et la perd en émettant un photon d’énergie \(h~\nu\)
4.2. Spectre en absorption
Quand on envoie de la lumière dans un gaz, celui-ci absorbe les photons correspondant à [\(h\nu_0~;~h\nu\)] et on observe des raies d’absorption.
5. Spectre de l’hydrogène
Le spectre de l’hydrogène est le plus simple à étudier.
On observe 4 raies \(\{H_{\alpha}~,H_{\beta}~,~H_{\gamma}~,~H_{\delta} \}\) dans le domaine visible.
Dans l’ultraviolet les raies se resserrent.
Balmer qui a étudié ces spectres a été conduit à donner le nombre d’onde \(\sigma\) sous forme de séries qui portent des noms différents suivant les domaines dans lesquels on opère : \[\sigma=\frac{1}{\lambda}=R~\Big\{\frac{1}{m^2}-\frac{1}{n^2}\Big\}\]
\(R=109677,581~cm^{-1}\) est la constante de Rydberg.
\[\begin{aligned} &\text{UV}& &\text{Visible}& &\text{IR}& &\text{IR lointain}\\ &m=1,~n=2& &m=2,~n=3& &m=3,~n=4& &m=4,~n=5\\ &Lyman& &Balmer& &Paschen& &Brackett \end{aligned}\]
Le principe de combinaison des raies
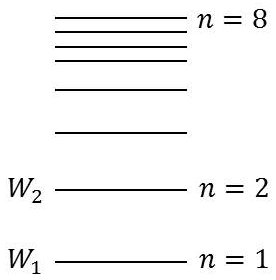 L’émission d’un photon correspond à une perte d’énergie : \[W=h~\nu=\frac{h~c}{\lambda}\]
L’émission d’un photon correspond à une perte d’énergie : \[W=h~\nu=\frac{h~c}{\lambda}\]
L’atome peut passer brusquement d’un état \(W_m\) à un état \(W_n\).
Il s’agit d’un saut quantique et d’après le principe de conservation de l’énergie : \[h~\nu=W_m-W_n=\frac{h~c}{\lambda}\]
D’où : \[\sigma=\frac{1}{\lambda}=\frac{1}{h~c}~(W_m-W_n)\]
En identifiant : \[\sigma=\frac{R}{m^2}-\frac{R}{n^2}\quad\Rightarrow\quad W=-\frac{R~h~c}{n^2}\]
Pour \(n = 1\), on retrouve le niveau fondamental : \[W=-R~h~c\]

